Лаб_1 структ и семант меры информации. Структурные и статистические меры информации

• Название: Структурные и статистические меры информации
• Дата: 14.04.2022
• Размер: 49.97 Kb.
• Имя файла: Лаб_1 структ и семант меры информации.docx
• Тип: Лабораторная работа; #472495

Министерство образования и науки Республики Казахстан
Карагандинский технический университет


Кафедра информационных технологий и безопасности


Кан О.А.


Лабораторная работа № 1
по дисциплине

«Информационные основы защиты информации»
Специальность: 6В06301 – «Системы информационной безопасности»


Караганда 2022

Лабораторная работа № 1
Тема: Структурные и статистические меры информации.
Цель работы: Исследование структурных и статистических методов измерения информации.
Краткие сведения из теории
Структурная мера информациирассматривает строение массивов информа­ции и их измерение простым подсчетом информационных элементов или комбинаторным методом. При использовании структурных мер информации учитывается толь­ко дискретное строение сообщения и количество содержащихся в нем ин­формационных элементов (символов). К структурным мерам информации относятся: геометрическая, комбинаторная и аддитивная.

Геометрическая мера информации употребляется в измерении длины, площади или объёма информационного массива в единицах дискретных элементов (сообщений) этого массива. 

Комбинаторная мера информации употребляется для оценки возможностей систем, в которых передача и хранение информации осуществляется при помощи различных комбинаций из набора сообщений. Сопоставление сообщениям из большого их множества (алфавита) комбинаций из других сообщений меньшего, множества (алфавита) является одним из способов кодирования, а сами комбинации (группы сообщений, символов) обычно называются кодовыми комбинациями.

Аддитивная мера информации (мера Хартли) используется для количественной оценки данных, полученных при измерениях, для оценки информационной емкости технических и других систем, а также различных документов, графической информации и в других случаях, где можно различать конечное число состояний.

Р. Хартли в 1928 году предложил формулу для измерения количества информации для равновероятных сообщений:

I = log₂ N

т. к. каждое из N событий имеет равновероятный исход (р = 1/N), то получим:

I = log₂ N = log₂ (1 / р) = - log₂ р.
Для N=2 получим I =1. Эту единицу назвали бит (от англ. Binary digit).

Данная формула даёт аналитическое определение бита по Хартли: это количество информации, которое содержится в одном двоичном разряде (цифре).

Алфавитный подход к измерению количества информации основан на подсчете числа символов в сообщении. При алфавитном подходе к определению количества информации отвлекаются от содержания информации и рассматривают информационное сообщение как последовательность знаков определенной знаковой системы.

Для решения задач по измерению количества информации в полученном сообщении используются следующие формулы:

N = 2ⁿ

где N - мощность алфавита (количество символов алфавита),

n – количество информации в одном символе.

 

I = K*n

где I – количество информации в сообщении,

K - количество символов в сообщении.
Пример. Для записи текста используются только строчные буквы русского алфавита и “пробел” для разделения слов. Какой информационный объем имеет текст, состоящий из 2000 символов?

Решение. В русском алфавите 33 буквы. Сократив его на две буквы (“ё” и “й”) и введя символ пробела, получаем число символов - 32. Используя формулу N = 2ⁿ получим

N = 32 = 2⁵

Отсюда: n = 5 бит – количество информации каждого символа. Тогда информационный объем всего текста равен:

I = 2000 · 5 = 10 000бит
В качестве основной характеристики сообщения теория информации принимает величину, называемую количеством информации. Для практического использования понятия информации необходимо научиться измерять количество информации.

Количество информации – это количество сведений, содержащихся в том или ином информационном элементе (в символе кода или сообщении).

Единица количества информации - двоичная цифра или бит. 1 бит - такое количество информации, которое содержит сообщение, уменьшающее неопределенность знаний в два раза. 

Величина, характеризующая количество неопределенности в теории информации обозначается символом H и имеет название энтропия.

В 1948 г. Клод Шеннон предложил формулу для вычисления количества информации для событий с различными вероятностями.

Если I - количество информации, N - количество возможных событий, р_i - вероятности отдельных событий, то количество информации для событий с различными вероятностями можно определить по формуле: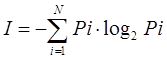

Максимального значения количество информации достигает при равновероятных событиях. При этом оно равно: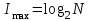

При наличии независимых источников информации с N1 и N2 числом возможных сообщений


I (N) = log N = log N1*N2 = log N1 + log N2,


т.е. количество информации, приходящееся на одно сообщение, равно сумме количеств информации, которые были бы получены от двух независимых источников, взятых порознь.

Клод Шеннон определил информацию, как снятую неопределенность. Точнее сказать, получение информации – это необходимое условие для снятия неопределенности. Неопределенность возникает в ситуации выбора. Величина, характеризующая количество неопределенности в теории информации обозначается символом H и имеет название энтропия.

Энтропия (H) – мера неопределенности, выраженная в битах. Количество информации I и энтропия H характеризуют одну и ту же ситуацию, но с качественно противоположенных сторон. I – это количество информации, которое требуется для снятия неопределенности H. Когда неопределенность снята полностью, количество полученной информации I равно изначально существовавшей неопределенности H.

Поэтому в формулах для расчета энтропии H, когда речь идет о полном снятии неопределенности, можно H  поменять на I. Расчет энтропии в этом случае производится по формуле Шеннона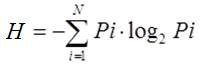

Пример. Пусть в некотором учреждении состав работников распределяется так: три женщины, один мужчина. Тогда неопределенность относительно того, кого вы встретите первым, зайдя в учреждение, будет рассчитана следующим рядом действий.

	Pi	1/Pi	Log2(Pi)	Pi*log2(Pi)
Женщина	3/4	4/3	0.42	0.31
Мужчина	1/4	4/1	2	0.5

В результате получим энтропию H = 0.31+0.5 = 0.81 бит.
Порядок выполнения работы

1. 
   Изучить теоретический материал.
   
2. 
   Выполнить задания.
   
3. 
   Ответить на контрольные вопросы.
   

Задание 1

Решите следующие задачи на определение количества информации.

• 
  Сообщение, записанное буквами из 16 символьного алфавита, содержит 7 символов. Найти количество информации в сообщении.
  
• 
  Алфавит содержит 8 букв. Найти количество информации, которое несут 5 букв этого алфавита.
  
• 
  В коробке лежат 10 красных шариков и 16 синих шариков. Вынули один шарик. Найти количество информации, что это синий шарик.
  

Задание 2

Источник сообщений выдает символы из алфавита A={a1, a2, a3, a4} с вероятностями:

P1=0.2; P2=0.3; P3=0.1; P4=0.4.

Найти количество информации. Все вычисления выполнить в программе MS Excel.
Задание 3

Выберите вариант задания и решите в MS Excel  задачу. В коробке лежат X красных, Y желтых, Z синих шаров. Какое количество информации несет сообщение о цвете вынутого шарика?
Варианты заданий

№ варианта	X	Y	Z
1	9727	16154	8407
2	15463	30981	4960
3	8462	28728	7733
4	8431	22394	6334
5	7556	13181	8184
6	11873	31755	8086
7	14832	20337	5737
8	13899	19917	4307
9	8908	26594	4248
10	9272	28438	8365
11	14887	19417	4478
12	15798	14733	7166

Задание 4

Выберите вариант задания и для заданного текста (количество символов в тексте М) найдите:

1) Мощность алфавита (К) источника (исходя из заданного текста);

2) Количество появлений каждой i-ой буквы в тексте (n_i);

3) Определите для каждой буквы алфавита вероятность ее появления по следующей формуле: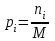


4) Для каждой буквы алфавита найти значение энтропии (количества информации), содержащееся в i-ой букве по формуле: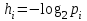


5) Вычислите энтропию источника русских букв по формуле: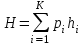



6) Определите максимальное значение энтропии источника при условии, что появление всех символов равновероятно.

7) Постройте график зависимости энтропии буквы h_i от вероятности ее появления p_i.

8) Все вычисления и график выполнить в программе MS Excel. Примерный вид расчета представлен в таблице 2.
Таблица 2.

	А	B	C	D	E	F
1
2		Буквы алфавита	Количество символов М	Pi	Энтропия буквы hi	Энтропия источника H
3		А	4	0,08
4		Б	2	0,04
…		…	…	…	…	…
33		Я	3	0,06
34		пробел	9	0,12
35			Значение М	1		Значение H

В ячейке С35 формула = СУММ(С3:С34)

В ячейках D3-D34 формула = Ci/C35 (i – меняется от 3 до 34)

В ячейке D35 формула = СУММ(D3:D34)

В ячейках E3-E34 формула =-log(Di;2) (i – меняется от 3 до 34)

В ячейках F3-F34 формула =Ei*Di (i – меняется от 3 до 34)

В ячейке F35 формула = СУММ(F3:F34)
Варианты заданий

1. 
   В Карагандинской области работают предприятия по добыче угля, машиностроения, металлообработки и пищевой промышленности.
   
2. 
   Для обнаружения и исправления ошибок, возникающих при передаче сообщений, применяют корректирующие коды.
   
3. 
   На сегодняшний день Караганда является одним из крупнейших промышленных, научных и культурных центров Казахстана.
   
4. 
   Семантической информацией называют информацию, содержащуюся в высказываниях и передаваемую через значения единиц речи.
   
5. 
   Измерительной информацией называют информацию о значениях физических величин, а также данные о погрешности измерений.
   
6. 
   Ключевой информацией называют такие новые сведения, которые не могут быть подсказаны ни контекстом, ни ситуацией.
   
7. 
   Документальная информация закрепляется посредством какой-либо знаковой системы на бумаге или ином материальном носителе.
   
8. 
   Генетическая информация определяет морфологическое строение, рост, развитие, обмен веществ, а также иные признаки организма.
   
9. 
   Деятельность по сбору и обработке существующей и созданию новой информации называется информационной деятельностью.
   
10. 
    Экономическая информация – это документированные сведения, отражающие состояние экономических процессов.
    
11. 
    Если же под воздействием помех разрешенная кодовая комбинация перешла в другую разрешенную комбинацию, то ошибка не будет обнаружена.
    
12. 
    В статистической теории информации в качестве меры количества информации используют энтропию.
    

Содержание отчета

1. 
   Титульный лист.
   
2. 
   Результаты выполненных работ.
   
3. 
   Ответы на контрольные вопросы.
   

Контрольные вопросы

1. Какая мера используется для количественной оценки информационной емкости технических систем?

2. Какую формулу предложил Р. Хартли для измерения количества информации?

3. Какую формулу предложил Клод Шеннон для вычисления количества информации и энтропии?

4. В каком случае формула Шеннона совпадает с формулой Хартли?

5. Что такое энтропия?