 СУММАТИВНОЕ ОЦЕНИВАНИЕ СУММАТИВНОЕ ОЦЕНИВАНИЕ
ЗА РАЗДЕЛ «СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА»
Подраздел
|
Тригонометрические функции острого угла в прямоугольном треугольнике. Теорема Пифагора. Основные тригонометрические тождества. Решение прямоугольных треугольников.
|
Цель обучения
|
8.1.3.2 знать определения синуса, косинуса, тангенса и котангенса углов через отношения сторон в прямоугольном треугольнике;
8.1.3.3 доказывать и применять теорему Пифагора;
8.1.3.24 находить значения sin𝛼, cos𝛼, t𝑔𝛼 и ct𝑔𝛼 по данному значению одного из них;
8.1.3.8 находить стороны и углы прямоугольного треугольника по двум заданным элементам.
|
Критерий оценивания
|
Обучающийся
определяет синус, косинус, тангенс и котангенс углов через отношения сторон в прямоугольном треугольнике;
решает задачи с помощью теоремы Пифагора;
находит значения тригонометрических функций по данному значению одной из них;
решает прямоугольный треугольник.
|
Уровень мыслительных навыков
|
Применение.
|
Время выполнения
|
25 минут
|
ЗАДАНИЯ
Оценивание заданий работы
|
№ задания
|
1
|
2
|
3
|
4
|
Количество баллов
|
4
|
2
|
4
|
5
|
Всего баллов
|
15 баллов
|
ВАРИАНТ 1
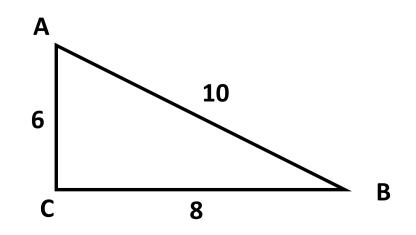
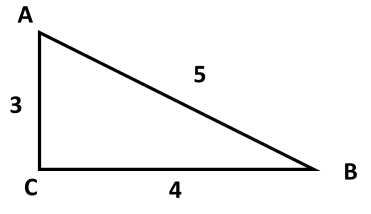
Используя данные рисунка, найдите синус, косинус, тангенс и котангенс угла А треугольника АВС с прямым углом С.
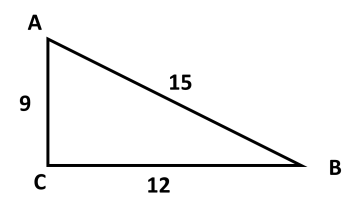
Найдите гипотенузу прямоугольного треугольника, если катеты соответственно равны 8 см и 11 см.
Найдите значение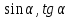 и и 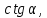 если если 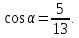
Архитектурное сооружение монумент «Байтерек» считается символом обновления Казахстана. Оно представляет собой высокую металлическую конструкцию с огромным позолоченным стеклянным шаром на вершине. Высота монумента составляет 97 м, а с шаром, венчающим конструкцию - 105 м. Монумент виден из точки А на поверхности земли, под углом 60°. Найдите расстояние от точки А до основания монумента и до его самой высокой точки.
ВАРИАНТ 2
Используя данные рисунка, найдите синус, косинус, тангенс и котангенс угла А треугольника АВС с прямым углом С.
Найдите гипотенузу прямоугольного треугольника, если катеты соответственно равны 9 см и 17 см.
Найдите значение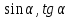 и и 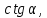 если если 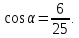
«Хан Шатыр»— крупный торгово-развлекательный центр в столице Казахстана Нур-Султане, является самым большим шатром в мире высотой 150 м. «Хан Шатыр» вошёл в Книгу рекордов Гиннесса. Торгово – развлекательный центр виден из точки А на поверхности земли, под углом 60°. Найдите расстояние от точки А до основания шатра и до его самой высокой точки.
ВАРИАНТ 3
Используя данные рисунка, найдите синус, косинус, тангенс и котангенс угла А треугольника АВС с прямым углом С.
Найдите гипотенузу прямоугольного треугольника, если катеты соответственно равны 7 см и 11 см.
Найдите значение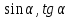 и и 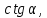 если если 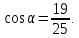
Монумент Независимости - грандиозное сооружение, возвышающееся на центральной площади города Алматы. Высота стелы, увенчанной шестиметровой фигурой «Золотого человека», изображенного в виде правителя, который управляет крылатым барсом, составляет 28 м. Монумент виден из точки А на поверхности земли, под углом 60°. Найдите расстояние от точки А до основания шатра и до его самой высокой точки.
ВАРИАНТ 4
Используя данные рисунка, найдите синус, косинус, тангенс и котангенс угла А треугольника АВС с прямым углом С.
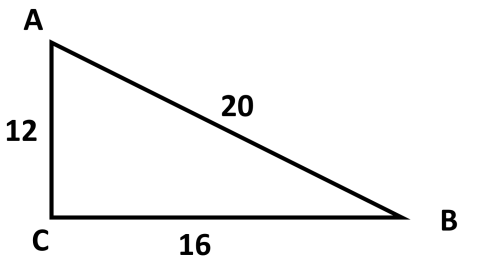
Найдите гипотенузу прямоугольного треугольника, если катеты соответственно равны 13 см и 7 см.
Найдите значение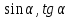 и и 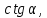 если если 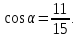
Монумент «Казак Ели» - это одна из достопримечательностей Нур-Султана, расположенный в центральной части города на площади Независимости. Высота белоснежной стелы составляет 91 метр и именно эта цифра напоминает о годе, когда Казахстан стал независимой республикой. Монумент виден из точки А на поверхности земли, под углом 60°. Найдите расстояние от точки А до основания монумента и до его самой высокой точки.
Критерий оценивания
|
№ задания
|
Дескриптор
|
Балл
|
Обучающийся
|
Определяет синус, косинус, тангенс и котангенс углов через отношения сторон в прямоугольном треугольнике
|
1
|
определяет синус угла через отношения сторон в прямоугольном треугольнике;
|
1
|
определяет косинус угла через отношения сторон в прямоугольном треугольнике;
|
1
|
определяет тангенс угла через отношения сторон в прямоугольном треугольнике;
|
1
|
определяет котангенс угла через отношения сторон в прямоугольном треугольнике.
|
1
|
Решает задачу с помощью теоремы Пифагора
|
2
|
выполняет рисунок по условию задачи;
|
1
|
применяет теорему Пифагора;
|
1
|
Находит значения тригонометрических функций по данному значению одной из них
|
3
|
записывает основное тригонометрическое тождество;
|
1
|
находит значение sinɑ;
|
1
|
находит значение tgɑ;
|
1
|
находит значение ctgɑ.
|
1
|
Решает прямоугольный треугольник
|
4
|
выполняет рисунок по условию задачи;
|
1
|
применяет соотношение для нахождения расстояния от точки А до основания монумента;
|
1
|
находит расстояние от точки А до основания монумента;
|
1
|
применяет соотношение нахождения расстояния от точки А до самой высокой точки монумента;
|
1
|
находит расстояние от точки А до самой высокой точки монумента.
|
1
|
Всего баллов 15
|
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА»
ФИ УЧАЩЕГОСЯ_____________________________________________________
Критерий оценивания
|
Уровень учебных достижений
|
Низкий
|
Средний
|
Высокий
|
Определяет синус, косинус, тангенс и котангенс углов через отношения сторон в прямоугольном треугольнике
|
Затрудняется в определении тригонометрических функций через отношения сторон в прямоугольном треугольнике
|
Допускает ошибки при определении синуса/ косинуса/ тангенса угла
|
 Определяет тригонометрические функции через отношения сторон в прямоугольном треугольнике Определяет тригонометрические функции через отношения сторон в прямоугольном треугольнике
|
Решает задачи с помощью теоремы Пифагора
|
Затрудняется в применении теоремы Пифагора
|
Применяет теорему Пифагора. Допускает вычислительные ошибки
|
 Применяет теорему Пифагора Применяет теорему Пифагора
|
Находит значения тригонометрических функций по данному значению одной из них
|
Затрудняется в нахождении значений тригонометрических функций по данному значению одной из них
|
Записывает соотношения для нахождения тригонометрических функций. Допускает вычислительные ошибки
|
 Находит значения тригонометрических функций по данному значению одной из них Находит значения тригонометрических функций по данному значению одной из них
|
Решает прямоугольный треугольника
|
Затрудняется в нахождении сторон и углов прямоугольного треугольника по двум заданным элементам
|
Применяет верные соотношения для нахождения сторон и углов прямоугольного треугольника. Допускает вычислительные ошибки
|
 Находит стороны и углы прямоугольного треугольника по двум заданным элементам Находит стороны и углы прямоугольного треугольника по двум заданным элементам
|
СУММАТИВНОЕ ОЦЕНИВАНИЕ
ЗА РАЗДЕЛ «ПЛОЩАДЬ»
Подраздел
|
Площадь фигуры и ее свойства. Площади четырёхугольников и треугольников
|
Цель обучения
|
8.1.3.10 знать определения равновеликих и равносоставленных фигур
8.1.3.12 выводить и применять формулы площади треугольника
8.1.3.13 выводить и применять формулы площади трапеции
|
Критерий оценивания
|
Обучающийся
Применяет определения равновеликих и равносоставленных фигур
Применяет формулы площади треугольника
Применяет формулы площади трапеции
|
Уровень мыслительных навыков
|
Применение.
Навыки высокого порядка
|
Время выполнения
|
25 минут
|
ЗАДАНИЯ
Оценивание заданий работы
|
№ задания
|
1
|
2
|
3
|
Количество баллов
|
4
|
4
|
6
|
Всего баллов
|
14 баллов
|
1 ВАРИАНТ
1. Докажите, что прямоугольник АВСД и параллелограмм ЕВСК , изображенные на рисунке, равновеликие и равносоставленные.
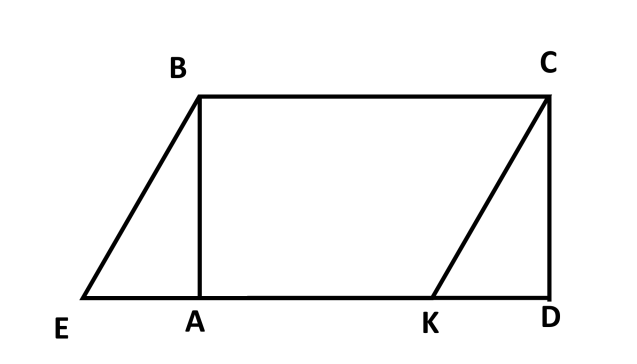
2. Площадь треугольника АВС равна 40 см2. Найдите высоту ВЕ, если АС равна 8 см.
3. Основания трапеции равны 5 см и 15 см, а боковая сторона равная 12 см, образует с одним из оснований трапеции угол равный 300. Найдите площадь трапеции.
2 ВАРИАНТ
1. Докажите, что прямоугольник АВСД и треугольник АКД , изображенные на рисунке, равновеликие и равносоставленные, если МР средняя линия треугольника АКД.
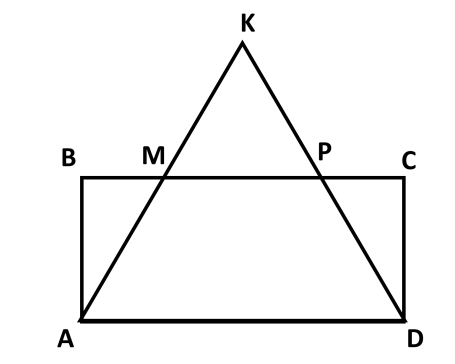
2. Площадь треугольника АВС равна 49 см2. Найдите высоту АВ, если ВС в два раза больше АВ и определите вид треугольника.
3. В равнобедренной трапеции, угол при основании равен 450 , а основания равны 3см и 7 см. Найдите площадь трапеции.
3 ВАРИАНТ
1. Докажите, что параллелограмм АВСД и параллелограмм АВМК , изображенные на рисунке, равновеликие и равносоставленные, если ДС ׀׀АВ ׀׀КМ
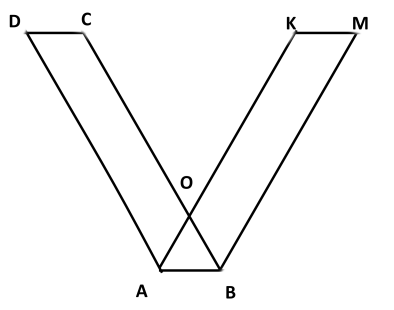
2. Площадь треугольника АВС равна 108 см2. Найдите высоту ВН, если ВС=АВ=15 см, а АС=18 см и определите вид треугольника
3. В прямоугольной трапеции угол при основании равен 450. Меньшее основание равно 7 см., высота равна 8 см. Найдите площадь трапеции.
4 ВАРИАНТ
1. Докажите, что равнобедренная трапеция АВСД и прямоугольник МВКД, изображенные на рисунке, равновеликие и равносоставленные.
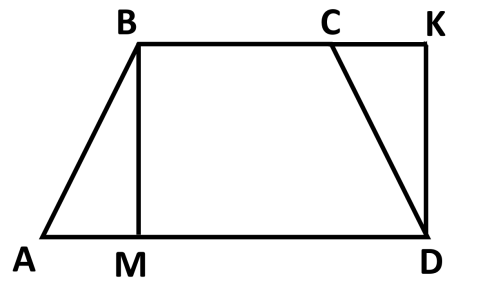
2. Найдите высоту треугольника проведенную к меньшей стороне , если стороны равны 8 см, 10 см и 14 см.
3. Найдите площадь трапеции АВСД, если АВ равен 5 см., ВС равен 4 см., СД равен 4 см, угол Д равен 900.
Критерий оценивания
|
№ задания
|
Дескриптор
Обучащийся
|
Балл
|
Применяет определения равновеликих и равносоставленых фигур
|
1
|
Определяет площадь первой фигуры
|
1
|
Определяет площадь второй фигуры
|
1
|
Применяет определение равновеликих фигур
|
1
|
Определяет равносоставленность фигур и обосновывает свой ответ
|
1
|
Применяет формулы площади треугольника
|
2
|
выполняет рисунок по условию задачи
|
1
|
определяет вид треугольника
|
1
|
применяет формулы площади треугольника
|
1
|
находит высоту треугольника
|
1
|
Применяет формулу площади трапеции
|
3
|
выполняет рисунок по условию задачи
|
1
|
определяет вид треугольника, образованного высотой и боковой стороной
|
1
|
применяет свойство прямоугольного треугольника
|
1
|
находит высоту трапеции
|
1
|
применяет формулу площади трапеции
|
1
|
находит площадь трапеции
|
1
|
Всего баллов
|
14
|
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА РАЗДЕЛ «ПЛОЩАДИ»
ФИ УЧАЩЕГОСЯ________________________________________________________________
Критерий оценивания
|
Уровень учебных достижений
|
Низкий
|
Средний
|
Высокий
|
Применяет определения равновеликих и равносоставленных фигур
|
Затрудняется в применении определения равновеликих и равносоставленных фигур
|
Применяет определение равновеликих фигур. Допускает ошибки в обосновании равносоставленных фигур.
|
Верно применяет определение равновеликих и равносоставленных фигур
|
Применяет формулы площади треугольника
|
Затрудняется в применении формул площади треугольника
|
Применяет формулы площади треугольника. Допускает вычислительные ошибки.
|
Верно решает задачи на применение формул площади треугольника.
|
Применяет формулы площади трапеции.
|
Затрудняется в применении формул площади трапеции
|
Применяет формулы площади трапеции. Допускает вычислительные ошибки.
|
Верно, решает задачи на применение формул площади трапеции.
|
СУММАТИВНОЕ ОЦЕНИВАНИЕ ЗА РАЗДЕЛ
«ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ НА ПЛОСКОСТИ»
Подраздел
|
Метод координат на плоскости. Решение текстовых задач
|
Цель обучения
|
8.1.3.14 вычислять расстояние между двумя точками на плоскости по их координатам
8.1.3.15 находить координаты середины отрезка
8.1.3.17 знать уравнение окружности с центром в точке (a,b) и радиусом r: 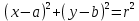
8.1.3.18 строить окружность по заданному уравнению
8.1.3.20 решение простейших задач в координатах
|
Критерий оценивания
|
Обучающийся
выбирает уравнение окружности с центром в точке 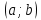 и радиусом и радиусом 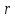 ; ;
применяет формулу нахождения координат середины отрезка;
применяет формулу нахождения расстояния между двумя точками на плоскости по их координатам;
Составляет уравнение окружности
Строит окружность по заданному уравнению
Решает простейшие задачи в координатах
|
Уровень мыслительных навыков
|
Применение.
Навыки высокого порядка
|
Время выполнения
|
25 минут
|
ЗАДАНИЕ
Оценивание заданий работы
|
№ задания
|
1
|
2
|
3
|
4
|
5
|
Количество баллов
|
2
|
3
|
3
|
2
|
4
|
Всего баллов
|
14 баллов
|
ВАРИАНТ 1
1) Выберите уравнение окружности, соответствующее рисунку:
А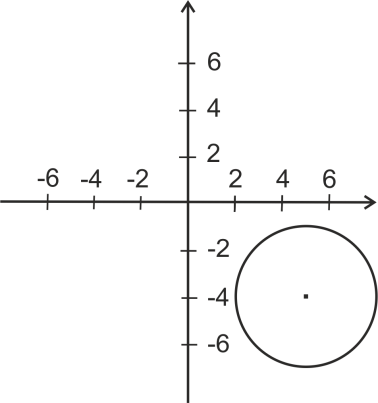 ) ) 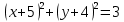 ; ;
B) 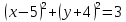 ; ;
C) 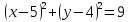 ; ;
D) 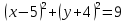
2) Найдите координаты точки B, если даны координаты следующих точек: 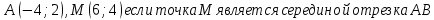
3) Постройте окружность, соответствующую уравнению:
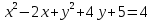
4) Принадлежат ли точки А(1;-6); В(-2;4) заданной окружности (х-1)2+(у+2)2=16
5)Даны вершины треугольника АВС: А(4;6), В(-4;0), С(4;-4). Определите вид треугольника и найдите его периметр.
ВАРИАНТ 2
1) Выберите уравнение окружности, соответствующее рисунку:
А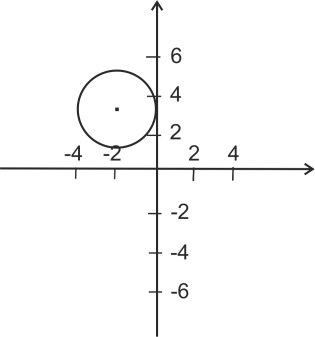 ) ) 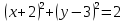 ; ;
B) 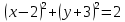 ; ;
C) 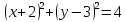 ; ;
D) 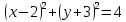
2) Найдите координаты точки B, если даны координаты следующих точек: 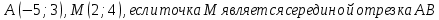
3) Постройте окружность, соответствующую уравнению:
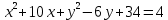
4) Принадлежат ли точки А(-3;5); В(-2;1) заданной окружности (х-2)2+(у-5)2=25
5)Даны вершины треугольника АВС : А(0;1), В(1;-4), С(5;2). Определите вид треугольника и найдите его периметр.
ВАРИАНТ 3
1) Выберите уравнение окружности, соответствующее рисунку:
А) 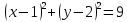 ; ;
B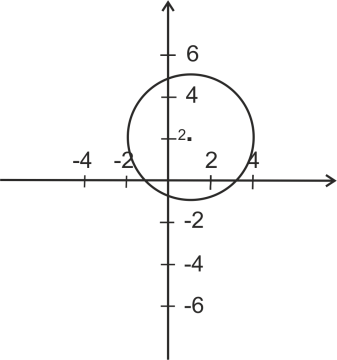 ) ) 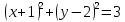 ; ;
C) 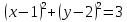 ; ;
D) 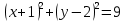
2) Найдите координаты точки B, если даны координаты следующих точек: 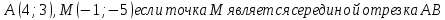
3) Постройте окружность, соответствующую уравнению:
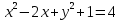
4) Принадлежат ли точки А(4;-6); В(-2;0) заданной окружности (х-4)2+(у-1)2=49
5)Даны вершины треугольника АВС : А(-4;1), В(-2;4), С(0;1). Определите вид треугольника и найдите его периметр.
ВАРИАНТ 4
1) Выберите уравнение окружности, соответствующее рисунку:
А) 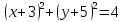 ; ;
B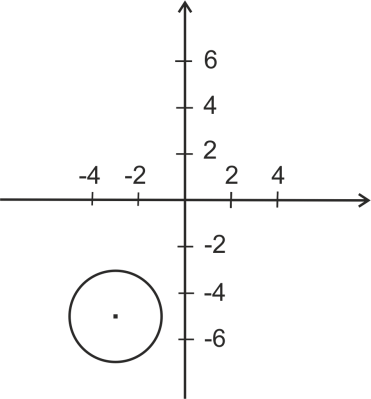 ) ) 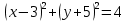 ; ;
C) 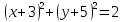 ; ;
D) 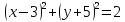
2) Найдите координаты точки B, если даны координаты следующих точек: 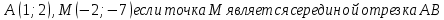
3) Постройте окружность, соответствующую уравнению:
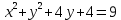
4) Принадлежат ли точки А(6;0); В(1;-3) заданной окружности (х-6)2+(у+3)2=9
5)Даны вершины треугольника АВС : А(-2;-3), В(1;4), С(8;7). Определите вид треугольника и найдите его периметр.
Критерий оценивания
|
№ задания
|
Дескриптор
|
Балл
|
Обучающийся
|
выбирает уравнение окружности с центром в точке 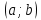 и радиусом и радиусом 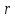 ; ;
|
1
|
находит r и координаты центра по рисунку
|
1
|
выбирает соответствующее уравнение
|
1
|
находит координаты конца отрезка, используя формулу нахождения координат середины отрезка;
|
2
|
составляет уравнение для нахождения координаты x
|
1
|
составляет уравнение для нахождения координаты y
|
1
|
записывает ответ в виде точки с координатами
|
1
|
строит окружность по заданному уравнению;
|
3
|
записывает стандартный вид уравнения окружности
|
1
|
находит r и координаты центра по рисунку
|
1
|
строит соответствующую окружность
|
1
|
определяет принадлежность точки окружности.
|
4
|
определяет принадлежность точки А окружности.
|
1
|
определяет принадлежность точки В окружности.
|
1
|
применяет формулу нахождения расстояния между двумя точками на плоскости по их координатам
решает текстовые задачи в координатах;;
|
5
|
применяет формулу для вычисления расстояние между двумя точками;
|
1
|
вычисляет длины всех сторон треугольника
|
1
|
определяет вид треугольника
|
1
|
вычисляет периметр треугольника
|
1
|
Всего баллов:
|
14
|
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА РАЗДЕЛ
«ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ НА ПЛОСКОСТИ»
ФИ УЧАЩЕГОСЯ_____________________________________________________
Критерий оценивания
|
Уровень учебных достижений
|
Низкий
|
Средний
|
Высокий
|
Применяет соотношения между координатами середины и координатами концов отрезка.
|
Затрудняется в применении соотношений между координатами середины и координатами концов отрезка
|
Применяет соотношения между координатами середины и координатами концов отрезка.
Допускает вычислительные ошибки
|
Верно, применяет соотношения между координатами середины и координатами концов отрезка
|
Составляет уравнение окружности.
|
Затрудняется в составлении уравнения окружности
|
Подставляет компоненты в уравнение окружности. Допускает ошибки со знаками / вычислительные ошибки
|
Верно, составляет уравнение окружности.
|
Строит окружность по заданному уравнению.
|
Затрудняется в построении окружности по заданному уравнению.
|
Определяет координаты центра и радиус окружности. Допускает погрешности в построении.
|
Верно, строит окружность по заданному уравнению.
|
Определяет принадлежность точки окружности..
|
Затрудняется в определении принадлежности точки окружности
|
Определяет принадлежность точки окружности . Допускает вычислительные ошибки
|
Верно, определяет принадлежность точки окружности
|
Решает простейшие задачи в координатах
|
Затрудняется в решении простейших задач в координатах.
|
Применяет соответствующие формулы. Допускает вычислительные ошибки
|
Верно, решает простейшие задачи в координатах.
|
|
 Скачать 208.82 Kb.
Скачать 208.82 Kb. СУММАТИВНОЕ ОЦЕНИВАНИЕ
СУММАТИВНОЕ ОЦЕНИВАНИЕ 
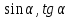 и
и 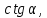 если
если 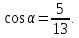

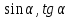 и
и 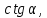 если
если 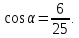

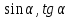 и
и 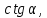 если
если 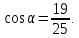

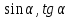 и
и 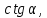 если
если 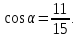




 )
) 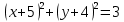 ;
;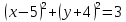 ;
;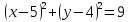 ;
;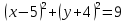
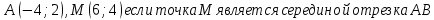
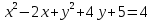
 )
) 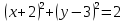 ;
;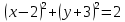 ;
;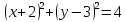 ;
;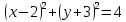
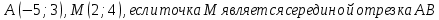
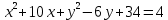
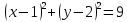 ;
; )
) 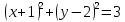 ;
;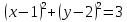 ;
;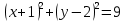
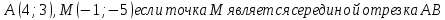
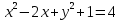
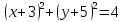 ;
; )
) 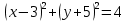 ;
;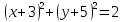 ;
;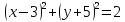
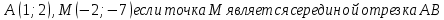
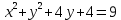

 Определяет тригонометрические функции через отношения сторон в прямоугольном треугольнике
Определяет тригонометрические функции через отношения сторон в прямоугольном треугольнике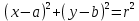
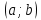 и радиусом
и радиусом 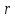 ;
;