Суперпозиция волны. Суперпозиция волны
 Скачать 0.79 Mb.
|
|
Суперпозиция волны. План: 1. Принцип суперпозиции волн. 2. Когерентные волны. Интерференция и дифракция волн. 3. Групповая скорость. Стоячие волны. 4. Звук волны, их высота, давление и энергия. Суперпозиция волны. 1. Принцип суперпозиции волн.Принцип суперпозиции (наложения) волн установлен на опыте. Он состоит в том, что в линейной среде волны от разных источников распространяются независимо, и накладываясь, не изменяют друг друга. Результирующее смещение частицы среды в любой момент времени равно геометрической сумме смещений, которые частица получит, участвуя в каждом из слагаемых волновых процессов. Согласно принципу суперпозиции накладываться друг на друга без взаимного искажения могут волны любой формы. В результате наложения волн результирующее колебание каждой частицы среды может происходить по любому сложному закону. Такое образование волн называется волновым пакетом. Скорость движения волнового пакета не совпадает со скоростью ни с одной из слагаемых волн. В этом случае говорят о скорости  волнового пакета. Скорость перемещения максимума группы волн (волнового пакета)называется групповой скоростью. Она равна скорости переноса энергии волнового пакета.На практике мы всегда имеем дело с группой волн, так как синусоидальных волн, бесконечных в пространстве и во времени, не существует. Любая ограниченная во времени и пространстве синусоидальная волна есть волновой пакет (его называют цуг волны). Групповая скорость такого пакета совпадает с фазовой скоростью бесконечных синусоидальных волн, результатом сложения которых он является. В общем виде связь между групповой и фазовой скоростями имеет вид:  .Электромагнитные волны.1. Электромагнитными волнами называются возмущения электромагнитного поля (т.е. переменное электромагнитное поле), распрострняющиеся в пространстве. Утверждение о существовании электромагнитных волн является непосредственным следствием решения системы уравнений Максвелла. Согласно этой теории следует, что переменное электромагнитное поле распространяется в пространстве в виде волн, фазовая скорость которых равна:  где  - скорость света в вакууме, , - электрическая и магнитная постоянные, , - соответственно диэлектрическая и магнитная проницаемость среды.2. Электромагнитные волны - поперечные волны. Векторы Е и Н поля электромагнитной волны взаимно перпендикулярны друг другу. Вектор скорости волны  и векторы Е и Н образуют правую тройку векторов (Рисунок 2.1.4).Для сравнения ориентации тройки векторов 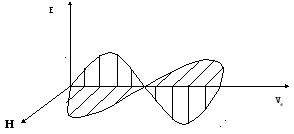, Е и Н на рисунке приведено расположение осей декартовой системы координат. Такое сопоставление уместно и в дальнейшем будет использовано для определения проекций векторов Е и Н на координатные оси.Р  исунок 2.1.4Взаимно перпендикулярные векторы Е и Н колеблются в одной фазе (их колебания синфазные). Модули этих векторов связаны соотношением:  которое справедливо для любой бегущей электромагнитной волны независимо от формы ее волновых поверхностей. 3.По форме волновых поверхностей волны могут быть плоские, эллиптические, сферические и т.д.. Монохроматической волной называется электромагнитная волна одной определенной частоты. Монохроматическая волна не ограничена в пространстве и во времени. В каждой точке электромагнитного поля монохроматической волны проекции векторов Е и Н на оси координат совершают гармонические колебания одинаковой частоты  . Например, дляплоской монохроматической волны, распространяющейся вдоль положительного направления оси ОУ, как показано на рисунке 2.1.3.,ее уравнение имеет вид: Такие волны называются плоско (или линейно) поляризованными волнами. Плоскость, в которой происходит колебание вектора Е называют плоскостью поляризации линейно поляризованной волны, а плоскость колебаний вектора Н – плоскостью колебаний. Ранее эти названия были обратными (см. [1]). 6. Все сказанное о стоячих волнах в упругих средах относится и к электромагнитным волнам. В этом случае, однако, волна характеризуется не одним вектором, а двумя взаимно перпендикулярными векторами Е и Н. Стоячая электромагнитная волна состоит из двух стоячих волн - магнитной и электрической, колебания которых сдвинуты по фазе на  .7. Энергия электромагнитных волн. Объемная плотность энергии электромагнитного поля в линейной изотропной среде задается соотношением:  с - скорость света в вакууме. В случае плоской линейно поляризованной монохроматической волны, распространяющейся вдоль положительного направления ОY, напряженность электрического поля задается уравнением:  соответственно объемная плотность энергии этой волны  Значение объемной плотности энергии волны меняется за период от 0 до  .Среднее за период значение энергии равно: .8. Вектор плотности потока энергии электромагнитной волны называется вектором Умова - Пойнтинга:  Для линейно поляризованной монохроматической волны вектор Пойнтинга направлен в сторону распространения волны и численно равен:  Интенсивность электромагнитной волны равна модулю среднего значения вектора Пойнтинга за период его полного колебания:  Интенсивностью электромагнитной волны называется физическая величина, численно равная энергии, переносимая волной за единицу времени через единицу площади поверхности, расположенной перпендикулярно к направлению распространения волны. Интенсивность бегущей монохроматической волны:  - фазовая скорость волны,  среднее значение объемной плотности энергии поля волны.Интенсивность света (электромагнитных волн, рассматриваемых в оптике) прямо пропорциональна квадрату амплитуды колебаний вектора напряженности Е поля световой волны. 2. Когерентные волны. Интерференция и дифракция волн. Интерференция явление, характерное для всякого движения. Интерференция света наложение световых пучков, при котором они в одних местах гасят друг друга, а в других усиливают. При ИС интенсивность суммарного пучка не равна сумме интенсивностей составляющих. Необходимым условием наблюдения ИС является когерентность пучков света. Когерентность колебаний (от лат. cohaerens находящийся в связи) наличие неизменных соотношений между фазами различных колебаний. Простейший случай когерентных колебаний два гармонических колебания с равными частотами и постоянной разностью фаз. В случае световых волн когерентные пучки могут быть получены только от одного и того же источника света. Для получения двух когерентных пучков свет, испускаемый источником, разделяется на два пучка, которые проходят различные пути и затем сводятся вместе. Результат ИС зависит от оптической разности хода интерферирующих пучков. Если один пучок проходит в среде с показателем преломления  геометрический путь  , а другой - в среде с показателем преломления  путь  , то разность хода  равна ,где  длина волны света, а  порядок интерференции, величина, определяющая результат И. Если целое число, то световые волны усиливают друг друга и возникают максимумы интенсивности. При разности хода, составляющей нечетное число полуволн  , наблюдается взаимное гашение волн и возникают минимумы интенсивности. Поскольку разность хода зависит от направления пучков, то в результате получаются светлые и темные полосы, каждая из которых соединяет точки с одинаковой разностью хода.Дифракцией называется любое отклонение распространения волн вблизи препятствий от законов геометрической оптики. Явления д. можно наблюдать, если на пути распространения электромагнитной волны находятся препятствия – непрозрачные тела произвольной формы или, если свет проходит через отверстия в непрозрачных экранах. Благодаря д. волны могут попадать в область геометрической тени. Если бы законы геометрической оптики выполнялись строго, то за экранами находились бы области тени, резко отграниченные от областей, куда свет попадает. Д. приводит к тому, что вместо резкой границы между светом и тенью получается сложная картина распределения интенсивности света. Д. явления тем сильнее выражены, чем меньше размеры экранов и отверстий в них или чем больше длина волны. Интерференцией называют явление, возникающее при наложении двух (или нескольких) световых волн одинакового периода в однородной изотропной среде, в результате чего происходит перераспределение энергии волн в пространстве. Томас Юнг в 1800 году сформулировал принцип суперпозиции (наложения) волн и объяснил интерференцию света. И сам термин “интерференция” был введен в науку тоже Юнгом. Т.Юнг родился 17 июня 1773 года. В двухлетнем возрасте научился читать, в девять лет изучил латынь и греческий язык. К четырнадцати годам знал десять языков, в том числе, древнееврейский, персидский и арабский. Сумел расшифровать египетские иероглифы. В 1795 году получил степень доктора медицины. За два года до этого Т.Юнг опубликовал работу по физической оптике “Наблюдения над процессом зрения”, в которой разработал теорию аккомодации глаза. Его основным трудом является “Лекции по натуральной философии”, который вышел в 1807 году в двух томах. Принцип суперпозиции позволил Т.Юнгу в 1802 году найти “простой и общий закон”, согласно которому “везде, где две части одного и того же света попадают в глаз по разным направлениям, свет становится или более сильным там, где разность путей есть целое кратное некоторой длины и наименее сильным в промежуточных состояниях интерферирующих частей, и эта длина различна для света различных цветов”. Этот принцип Т.Юнг подтвердил на опыте: солнечный свет, выходящий из небольшого отверстия в ставне окна, освещает экран, в котором кончиком булавки были сделаны два отверстия на небольшом расстоянии друг от друга. Свет, выходящий коническими пучками из обеих отверстий, перекрещивался в некоторой области светового поля за экраном, и на приемном экране появлялись светлые и темные полосы. Когда закрывалось одно из отверстий, то полосы исчезали и на приемном экране были видны лишь дифракционные кольца от другого отверстия (Т.Юнг знал явление дифракции и в 1801 году объяснил ее в одной из своих работ). Юнг измерил ширину полос и определил ту “некоторую длину”, которая фигурировала в его законе. Это были первые в истории физике определения длины волны, которая для красного света оказалась равной 0.7 микрона и 0.42 микрона для крайнего фиолетового. Интерференция света возникает при наложении когерентных волн. Когерентные волны – это волны, у которых одинаковые частоты (  разность фаз между колебаниями с течением времени не изменяется ( ) и колебания происходят в одной плоскости.Никакие два светящихся тела не могут быть когерентными источниками света. На самом деле, свет, исходящий от светящего тела (например, от нити электролампы), представляет собой совокупность множества ЭМВ, излучаемых отдельными частицами (атомами и молекулами) тела. Условия излучения этих частиц очень быстро и беспорядочно изменяются. Для того, чтобы два светящихся тела являлись когерентными источниками света, длины волн, излучаемых всеми частицами первого тела, должны отличаться по фазе от длин волн, излучаемых всеми частицами второго тела, все время на одно и тоже значение. Такое событие совершенно невероятно. Поэтому для получения когерентных источников свет “раздваивают” (рис.1а). 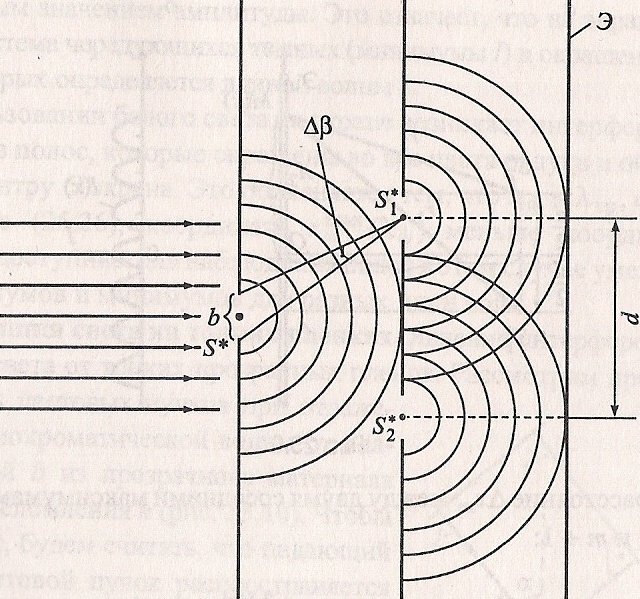 рис.1а Если в разности хода лучей ∆l укладывается целое число длин волн (четное число полуволн), 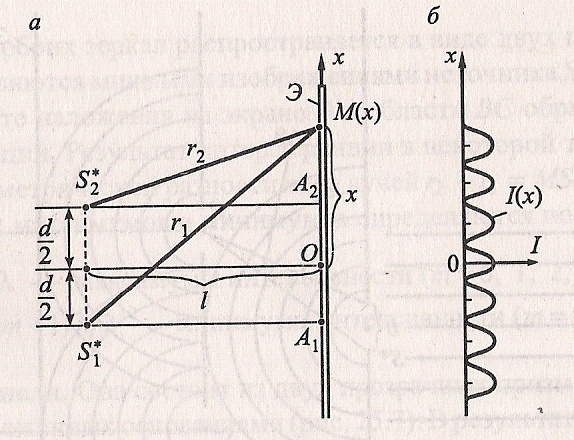 рис.1б то есть  (3)то в точке М будет максимум света (λ–длина волны; κ=0,1,2,…). Если же в ∆l укладывается нечетное число полуволн (не целое число длин волн), то  (4)то в точке М – минимум света. Максимумы света располагаются на расстоянии  (5)а минимумы:  (6)Эти максимумы и минимумы имеют вид светлых и, соответственно, темных полос (рис.2), параллельных друг другу.  (7)(7) – расстояние между соседними максимумами или минимумами. 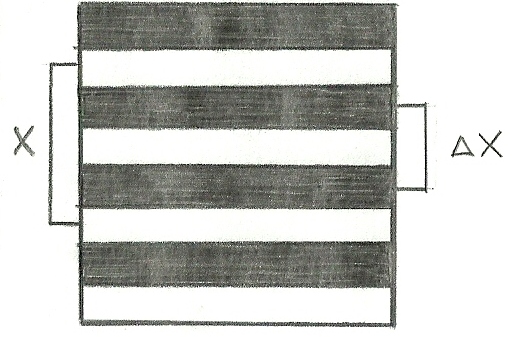 Начало формы Конец формы |