Суперпозиция волны. Суперпозиция волны
 Скачать 0.79 Mb. Скачать 0.79 Mb.
|
3. Групповая скорость. Стоячие волны.Принцип суперпозиции. Если свойства среды не изменяются под действием возмущений, создаваемых волной, то к ним применим принцип суперпозиции (наложения волн): при распространении в такой среде нескольких волн, каждая из них распространяется так, как будто другие волны отсутствуют, а результирующее смещение частицы среды равно геометрической сумме смещений частиц. Строго монохроматическаяволна имеет постоянную частоту. Будем рассматривать такие волны с учетом начальной фазы α: ξ = А0cos(ωt − kx + α). (1.5) Значение фазовой скорости этой волны V = ω/k или V = λν = λ/T. С помощью такой волны нельзя передавать сигнал, так как в любой точке волны сигналы одинаковы. Сигнал должен отличаться, быть знаком (меткой) на волне. Но тогда волна уже не будет описываться уравнением (1.5). Групповая скорость. Сигнал (импульс) можно представить (согласно теореме Фурье) в виде суперпозиции гармонических волн с частотами, заключенными в некотором интервале Δω. Суперпозиция волн, мало отличающихся друг от друга по частоте (т.е. ∆ω<<ω), называется волновым пакетом или группой волн (рис. 1.6). Выражение для группы волн имеет вид: 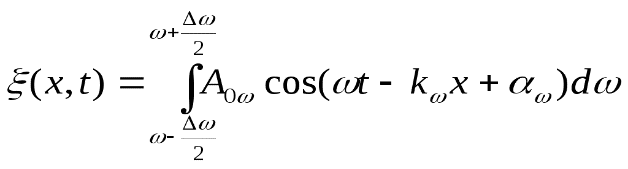 . (1.6) . (1.6)Здесь Р 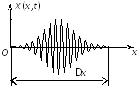 ис. 1.6 ис. 1.6начальные фазы волн, составляющих группу. Индекс Группе волн предписывают скорость u, с которой перемещается центр группы волн (волнового пакета), т.е. точка с максимальным значением Р 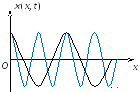 ис. 1.7 ис. 1.7Среды, для которых групповая скорость зависит от частоты, называются диспергирующими средами, т.е. средами, обладающими дисперсией. В недиспергирующей средевсе плоские волны, образующие пакет, распространяются с одинаковой фазовой скоростью V. Очевидно, что в данном случае направление скорости перемещения пакета совпадает с направлением скорости В диспергирующей средекаждая волна распространяется со своей скоростью, пакет с течением времени расплывается, его ширина увеличивается. Если дисперсия невелика, то расплывание происходит не слишком быстро и пакету можно приписать скорость u. Вместе с движением самого пакета происходит движение максимумов внутри пакета (рис. 1.8). Максимумы перемещаются со скоростью V, а пакет в целом – со скоростью u. Там, где фазы совпадают, наблюдается усиление амплитуды, при несовпадении фаз волны гасятся (результат интерференции). Групповая скорость u может отличаться от фазовой скорости V. Она может быть больше фазовой скорости, меньше ее или равной ей. В диспергирующей среде u ≠ V. Р  ис. 1.8 ис. 1.8Рассмотрим суперпозицию двух волн с одинаковыми амплитудами, распространяющихся в направлении оси OX с начальными фазами, равными нулю. 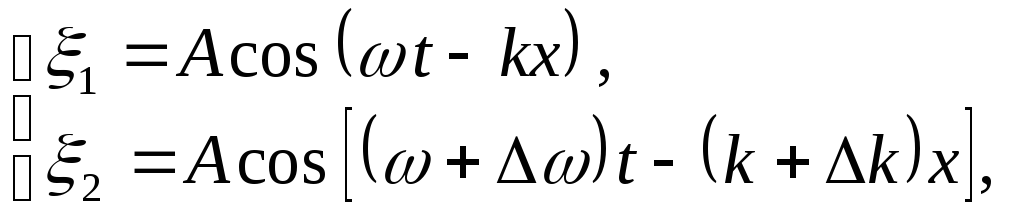 (1.7) (1.7)где k = ω/V1; (k + ∆k) = (ω + ∆ω)/V2 . Пусть При сложении этих волн получаем Здесь Каждый из этих максимумов рассматривается как центр соответствующей группы волн. Разрешив выражение (1.9) относительно отсюда следует, что т.е. максимумы амплитуды результирующей волны перемещаются со скоростью u. Выражение (1.11) представялет собой групповую скорость для случая, когда группа волн образована двумя составляющими. Для волнового пакета, состоящего из нескольких волн, мало отличающихся друг от друга по частоте, выражение (1.11) в пределе примет вид: Выражению (1.12) для групповой скорости можно придать другой вид. Заменив ω через Vk, представим (1.12) следующим образом Далее напишем Из соотношения Из этой формулы видно, что в зависимости от знака В отсутствие дисперсии Следует также отметить, что для акустических и электромагнитных волн в средах с резонансным поглощением, а также в средах с периодической структурой (кристаллы) возможна даже ситуация, при которой групповая скорость u направлена противоположно фазовой. Групповая скорость определяет скорость и направление переноса энергии волнами. Понятие групповой скорости играет важную роль и в физике, и в технике, поскольку все методы измерения скоростей распространения волн дают групповую скорость. Именно эта скорость фигурирует при измерении дальности в гидролокации, радиолокации, при зондировании атмосферы, при управлении космическими объектами, в теории связи и т.д. Однако понятие групповой скорости в средах с сильным поглощением энергии волны неприменимо. Для таких сред вводят величину, характеризующую скорость переноса энергии. Среды, в которых волны не поглощаются, называются прозрачными. В таких средах групповая скорости и скорость переноса энергии совпадают. Стоячие волны. Волны называются когерентными, если они имеют одинаковую частоту, разность их фаз не изменяется во времени. При сложении двух или нескольких когерентных волн, в разных точках среды, получается усиление или ослабление результирующей волны. Это явление называется интерференцией волн. Одним из примеров сложения волн служит наложение двух плоских волн, бегущих вдоль оси Оx в среде без затухания в противоположных направлениях с одинаковыми амплитудой и частотой. Выберем начало координат в точке, в которой обе волны имеют одинаковую начальную фазу, а отсчет времени начнем с момента, когда начальные фазы обеих волн равны нулю, т.е. ξ1 (x,t) =Asin(wt – kx), ξ2(x,t)= Asin(wt +kx). В этом случае результирующее смещение определяется формулой ξ (x,t) =Asin(wt – kx)+Asin(wt +kx)=2Asinwt∙ coskx=B(x) sinwt,(1.15) которая является уравнением стоячей волны. Такое сложение мы можем наблюдать при отражении волн от преград. Падающая на преграду волна и бегущая ей навстречу отраженная, накладываясь друг на друга, образуют стоячую волну. Из (1.15) видно, что в каждой точке этой волны происходят колебания той же частоты, что и у встречных волн, причем амплитуда В зависит от координаты х: В(х) = 2А cos kx = 2Acos2px/l. В тех точках, где 2px/l = np (n = 0,1,2,...), амплитуда В достигает максимума, равного 2А. Эти точки называются пучностями стоячей волны. Координаты пучностей равны хnуч = ±nl/2. В точках, где 2pх/l = ±(n+1/2)p, амплитуда В обращается в нуль. Эти точки называются узлами стоячей волны. Точки среды, находящиеся в узлах, колебаний не совершают. Координаты узлов равны xyз = ±(n ±½)l/2. Из формул для координат узлов и пучностей следует, что расстояние между соседними узлами (так же как и соседними пучностями) равно l/2. На границе раздела сред, где происходит отражение волны, может возникнуть узел или пучность, это зависит от соотношения плотностей сред. Если среда, от которой происходит отражение, менее плотная, то в месте отражения возникнет пучность (рис.1.9а), если более плотная – узел (рис.1.9б). 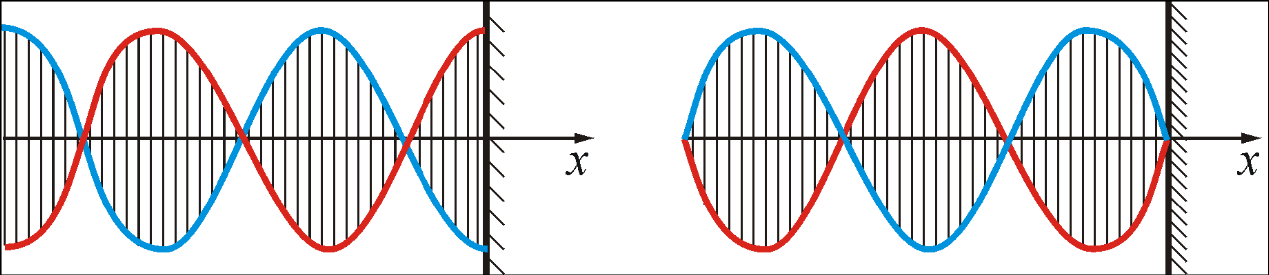 а) б) Рис. 1.9 Образование узла связано с тем, что волна, отражаясь от более плотной среды, меняет фазу на противоположную и у границы раздела сред происходит сложение колебаний с противоположными фазами, в результате чего получается узел. Если же волна отражается от менее плотной среды, то фаза не измененяется и у границы раздела сред колебания складываются с одинаковыми фазами, в результате чего образуется пучность. В случае стоячей волны переноса энергии колебаний нет, так как падающая и отраженная волны одинаковой амплитуды несут одинаковую энергию в противоположных направлениях. Поэтому полная энергия колебаний частиц среды результирующей стоячей волны, заключенной между узловыми точками, остается постоянной. 4. Звук волны, их высота, давление и энергия. Звуковые волны. Важным видом продольных волн являются звуковые волны. Так называются волны с частотами 17 – 20000 Гц. Учение о звуке называется акустикой. В акустике изучаются волны, которые распространяются не только в воздухе, но и в любой другой среде. Упругие волны с частотой ниже 17 Гц называются инфразвуком, а с частотой выше 20000 Гц – ультразвуком. Звуковые волны – упругие колебания, распространяющиеся в виде волнового процесса в газах, жидкостях, твердых телах. Избыточное звуковое давление. Уравнение звуковой волны. Уравнение упругой волны позволяет вычислить смещение любой точки пространства, по которому проходит волна, в любой момент времени. Но как говорить о смещении частиц воздуха или жидкости от положения равновесия? Звук, распространяясь в жидкости или газе, создает области сжатия и разряжение среды, в которых давление соответственно повышается или понижается по сравнению с давлением невозмущенной среды. Если Изменение избыточного давления для плоской звуковой волны (т.е. уравнение плоской звуковой волны) имеет вид: 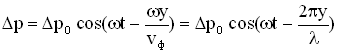 , (30.1) , (30.1)где y – расстояние от источника колебаний точки, избыточное давление в которой мы определяем в момент времени t. Если ввести величину избыточной плотности Ск Объективные и субъективные характеристики звука. Само слово “звук” отражает два различных, но взаимосвязанных понятия: 1)звук как физическое явление; 2)звук – то восприятие, которое испытывает слуховой аппарат (человеческое ухо) и ощущения, возникающие у него при этом. Соответственно характеристики звука делятся на объективные, которые могут быть измерены физической аппаратурой, и субъективные, определяемые восприятием данного звука человеком. К объективным (физическим) характеристикам звука относятся характеристики, которые описывают любой волновой процесс: частота, интенсивность и спектральный состав. В таблицу1. включены сравнительные данные объективных и субъективных характеристик. Таблица1.
Частота звука измеряется числом колебаний частиц среды, участвующих в волновом процессе, в 1 секунду. Интенсивностьволны измеряется энергией, переносимой волной в единицу времени через единичную площадь (расположенную перпендикулярно направлению распространению волны). Спектральный состав (спектр)звука указывает из каких колебаний состоит данный звук и как распределены амплитуды между отдельными его составляющими. Различают сплошные и линейчатые спектры. Для субъективной оценки громкости используются величины, называемые уровнем силы звука и уровнем громкости. Таблица 2 -Объективные характеристики механических волновых процессов.
Для характеристики величин, определяющих восприятие звука, существенными являются не столько абсолютные значения интенсивности звука и звукового давления, сколько их отношение к некоторым пороговым значениям. Поэтому вводятся понятие относительных уровней интенсивности и звукового давления. Для того, чтобы звуковая волна воспринималась на слух, необходимо, чтобы ее интенсивность превышала бы минимальную величину Уровень интенсивности (уровень силы звука) равен десятичному логарифму отношения интенсивности звука при данной частоте к интенсивности звука при той же частоте на пороге слышимости: 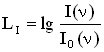 . .Громкость звука — субъективное восприятие силы звука (абсолютная величина слухового ощущения). Громкость главным образом зависит от звукового давления и частоты звуковых колебаний. Также на громкость звука влияют его тембр, длительность воздействия звуковых колебаний и другие факторы. Уровень громкостиравен десятичному логарифму отношения интенсивности звука при данной частоте к интенсивности звука при частоте 1000 Гц на пороге слышимости: 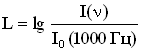 . .Единицей измерения уровня интенсивности является бел (Б): 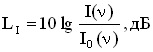 . .Если записать формулу для уровня громкости в виде 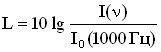 , то единицей измерения в СИ при таком определении величины является, единица, имеющая название фон. При частоте 1000 Гц шкала фонов и децибел совпадают, для других частот они различны. , то единицей измерения в СИ при таком определении величины является, единица, имеющая название фон. При частоте 1000 Гц шкала фонов и децибел совпадают, для других частот они различны.Уровень звукового давления равен произведению 20 на логарифм отношения звукового давления при данной частоте к звуковому давлению на пороге слышимости. Единицей измерения в данном случае является децибел. 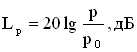 . . |
