Свч электротехнологических установок для модификации диэлектриков

• Название: Свч электротехнологических установок для модификации диэлектриков
• Дата: 01.05.2022
• Размер: 2.15 Mb.
• Имя файла: 1_00676 (1).docx
• Тип: Диссертация; #506934
• страница: 13 из 23

Камеры лучевого типа для обработки жидких и вязких полимерных материалов

1. Движениежидкостейвкамерахлучевоготипа

Нетепловая модификация жидких и вязких полимерных сред доказана исследованиями ряда авторов [13, 82]. Так, например, кратковременное пре- бывание смазочно-охлаждающих жидкостей (СОЖ), смазок триботехниче- сого назначения, а также синтетических смол, например эпоксидных, в СВЧ электромагнитном поле приводит к появлению в этих материалах новых по- лезных технологических свойств.

Рабочие камеры для нетепловой модификации всех этих диэлектриков, которые вслед за[6] будим называть жидкостями,могут работать в перио- дическом режиме, но очень часто предназначены для обработки диэлектри- ков в потоке (методический режим).

Тепловая модификация проточных сред в СВЧ электротермических ус- тановках обычно проводится в КБВ (рис. 4.7). В этих камерах можно полу- чить весьма равномерную термообработку объекта на уровнеК _стu < 1,2 – 1,3.




аб

Рис. 4.7. КБВ для модификации проточной среды: а– методического действия; б − пе- риодического действия.

Однако этим камерам присущи характерные для КБВ недостатки:

− существенное увеличение объема обрабатываемой жидкости может быть достигнуто, главным образом, построением КБВ на частоте 433 МГц

– наименьшей из разрешенных к применению в СВЧ электротехнологиче- ских установках. В этом случае у рабочей камеры будет наибольший диа- метр гидравлического канала, по которому протекает (прокачивается) обра- батываемая жидкость, однако при этом, во-первых, резко возрастают габа- риты, масса, а значит и цена такой рабочей камеры, а во-вторых, модифици- рующее воздействие пока что исследовалось только на частоте 2450 МГц;

− увеличить объем производимой продукции на рабочей частоте мож- но также увеличением расхода жидкости через гидравлический канал, но при этом потребуется для прокачки жидкости насос с большой производи- тельностью, а это скажется на экономической эффективности установки; к тому же, как показывает практика, в таких случаях рабочая камера начинает вибрировать, что может привести, например, к ослаблению крепежных вин- тов с неизбежным увеличением уровня СВЧ излучений в окружающее про- странство;

− если у жидкости tgδ

нагрузка.

<< 1, то на выходе КБВ должна быть балластная

Все эти недостатки удается устранить,

− применяя для нетепловой модификации жидких диэлектриков КЛТ, используя схемы КЛТ с несколькими излучающими системами, можно осу- ществить нетепловую модификацию жидкости с любой большой производи- тельностью;

− используя гидравлические каналы больших поперечных сечений, в том числе систем с открытым стоком (поток в лотке), можно избежать виб- рации гидравлической системы;

− применяя согласующего четвертьволнового трансформатора (см.

п. 3.1) можно обеспечить согласование КЛТ с СВЧ генератором;

− применяя приемный рупор за потоком, можно реализовать вариант гибридной установки.

Существенную роль в реализации модифицирующего воздействия в КЛТ играют особенности модифицируемой жидкости характер её движения в гидравлическом канале.

Как известно, жидкости подразделяются на ньютоновские (вода, рас- творы) и неньютоновские (расплавы полимеров, лакокрасочные материалы, вязкие среды) в зависимости от того, подчиняются они или нет закону тре- ния Ньютона [83].

Реологические кривые (кривые течения), изображающие зависимо-

сти градиента скорости течения жидкости

^υdот касательного напряжения

dn

τ, где n – направление, перпендикулярное движению жидкости, приведе- ны на рис. 4.8. Среди неньютоновских жидкостей различают дилатантные (кривая 1 рис.4.8), псевдопластичные (кривая 3 рис.4.8) и вязкопластичные (кривая 4 рис.4.8) жидкости. Примерами дилатантных жидкостей являются различные лакокрасочные материалы, псевдопластичных – расплавы поли- меров, вязкопластичных − суспензии и коллоидные растворы, состоящие из двух фаз, твердой и жидкой (например, битумные, изоляционные материалы, глинистые растворы).




Рис.4.8. Кривые течения жидкости: 2 – ньютоновские жидкости; 1, 3, 4 − неньютонов- ские жидкости(1- дилатантные; 3 – псевдопластичные; 4 - вязкопластичные)

Для характеристики гидравлических свойств ньютоновских жидкостей используют понятие кинематической вязкости проточной среды [83]

_=ν 1,79 �10⁻⁶ _,

1+ 0,0377Т+ 0,000221Т²

где ν в м² �;⁻Т¹ – температура жидкости в ^ºС.

Для характеристики реологических свойств неньютоновских жидко-

стей обычно пользуются понятием эффективной кажущейся вязкости

μ_э ,

используемой при расчетах по обычным формулам гидравлики ньютонов-

ских жидкостей, когда

μ_э и ν связаны между собой соотношением


э
μ

=ν,

ρ

где ρ− плотность жидкости.

У дилатантных жидкостей кажущаяся вязкость
μ_э с увеличением
υd dn

увеличивается, и эти жидкости при течении загустевают. У псевдопла-

стичных жидкостей

μ_э с увеличением

^dуменьшается, и эти жидкости при

dn

течении разжижаются.

Наконец, вязкопластичные жидкости совмещают в себе свойства как ньютоновской жидкости, так и твердого пластичного тела. Течение этих жидкостей начинается при напряжении, равном начальному напряжению сдвига τ (рис.4.8) и продолжается как у обычных ньютоновских жидкостей.

Величина начального напряжения сдвига зависит от времени нахождения вязкопластичной жидкости в покое. Это свойство (тиксотропия) необходи- мо учитывать при расчете рабочих камер для вязкопластичных жидкостей. В начальный момент вязкопластичная жидкость движется как целиком твердое тело с одинаковой скоростью по всему сечению канала. С увеличением пе- репада давления между концами канала скорость движения жидкости уве- личивается и можно говорить о структурном, ламинарном или турбулент- ном режимах её движения.

Режим течения жидкости играет принципиальную роль в гидравличе- ских и реологических расчетах. Так, обычно режим течения жидкости опре- деляется числом Рейнольдса

Re= ^dυ, (4.13)

где υ− скорость потока на рассматриваемом участке; d– диаметр трубы

(эквивалентный диаметр для трубы не круглого сечения).

Если Re<2200, то режим считается ламинарным; при

2,2�10³ < Re<

10⁴ − переходным, а при Re>

10⁴ − турбулентным[78]. В

обычных инженерных расчетах, как правило, считают режим ламинарным при Re < 2300 и при Re > 2300 турбулентным [83]. В случае вязкопластич- ных жидкостей структурное движение имеет место при наименьших перепа- дах давления, обеспечивающих движение жидкости по каналу. В этом слу- чае в ближайших к стенкам трубы частях потока развивается ламинарный режим, а центральная часть движется, как и при начале движения из состоя- ния покоя, подобно твердому телу. Чем больше перепад давления, тем шире зона ламинарного режима и тем меньше размеры центральной части потока. Чисто ламинарного режима без центральной части не бывает, и с ростом перепада давлений структурный режим переходит непосредственно в турбу- лентный. Обобщенное число Re, учитывающее как вязкие, так и пластиче- ские свойства жидкости, имеет вид

Re^�= ¹ ,

μ_э ρυd

₊ τ_н

6ρυ²

где усредненная скорость течения жидкости в трубе сечением S рассчиты- вается обычным путем

ЗдесьG– расход жидкости,
м³ с .

=υ . (4.14)


G
S

Развиваемое в КЛТ давление чаще всего позволяет получить структур- ное движение вязкопластичной жидкости. Критерием структурного движе- ния вязкопластичной жидкости является условие

υ < _кр,

где υ− скорость движения жидкости, рассчитываемая по (4.14),

^υкр
0=,25

^τ.^нЕсли υ >

ρg
_кр, то режим турбулентный. При этом

_G≈ πr<sup>4

�</sup>Δp− ⁴ Δp^�,

�

0

�
8 lμ^� 3 ^�

где ∆p
− приложенная разность давления;

∆p₀

≈ ^4τ0l; d, l, r– диаметр, дли-

d

на и радиус трубы,

^μпл⁼

μ_э− ^н.

υd dn

Что касается дилатантных и псевдопластичных жидкостей, то при ла- минарном режиме

G=.

3n

nrπⁿ

1 ₁

�^∆p�_n

3n+1 ^{� �}

_�2kl_�

где k, n− постоянные для данной жидкости, k определяет меру консистен- ции, причем чем выше вязкость, тем вышеk, а n характеризует степень неньютоновского поведения жидкости (для дилатантной жидкости n > 1, для псевдопластичной n < 1).

Для ньютоновских жидкостей при kµn1.

Движение жидкостей в КЛТ может быть рассмотрено лишь для кон- кретной схемы гидравлического канала и движения среды в рабочей камере. Гидравлические особенности проявляются в том случае, когда жидкость протекает в КЛТ по открытому желобу или в трубе благодаря их наклону к горизонту или поток создается каким-либо устройством (аппаратом), разви- вающим давление на входе в камеру. Заметим, что подобных задачах не возникает, если обрабатываемая жидкость транспортируется в КЛТ, напри-

мер, с помощью электропривода на конвейерной ленте в каких-либо отдель- ных ёмкостях.

Характером движения жидкости по гидравлической системе КЛТ ин- тересуются для определения давления, которое нужно создать на входе в гидравлическую систему, чтобы обеспечить при выбранной мощности СВЧ генератора заданный режим обработки. Чтобы найти это давление, разобьем гидравлический канал на характерные участки и для сечений 1 и 6 (рис.4.9) запишем уравнения Бернулли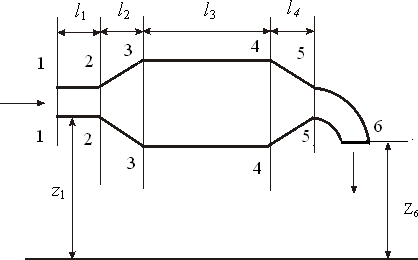


Рис. 4.9. Гидравлическая система для нетепловой модификации жидкости

p₁ α υ ² p₆ α ₆υ₆²

z₁ +

+ ¹¹ = z₆ + +

+ h, (4.15)

gρ2ggρ2g

где ₁ и ₆ − геометрическая высота сечений 1 и 6;

p₁и

p₆ − давления в се-

чениях 1 и 6;

υ₁ и υ₆ − средние скорости потока в сечениях 1 и 6; g− ускоре-

α υ ²

α ₆υ₆²

ние свободного падения;

11 _и

g2

_g2 − скоростные напоры в сечениях1

и 6: α₁ и α ₆ − коэффициенты Кориолиса в сечениях 1 и 6; h − потери напора на всем трубопроводе гидросистемы.

Поскольку α

1,03 - 1, 1, примем

α α=


1
2

1. 
   . На выходе из трубопровода
   

(сечение 6) абсолютное гидростатическое давление равно атмосферному,

следовательно, избыточное давление в этом сечении равно нулю, то есть

р⁶ = 0 . Тогда из уравнения (4.15) получим

gρ

�

�
�_υ6² _−υ ² �

где ∆

₁ − ₆ .

h₁ =zgρ^�p_2g¹

�

−+∆

^�, (4.16)

�

Для СВЧ энергии, подводимой к гидросистеме на участке между сече- ниями 3 и 4, по закону сохранения энергии

где

^{Р Р}отр^{+ Р}погл^{+ Р}прош^,
Р_отр= Г² Р,

^Рпогл⁼

Gсρ∆Θ


,
3

^Рпрош
РР

отр

^Рпогл ^,

∆Θ Θ₄ −Θ₃ , (4.17)

Θ ₃ Θ ₄

определяют температуру жидкости в сечениях 3 и 4; G

− объемный

3
расход жидкости на участке между сечениями 3 и 4.

Если в КЛТ применяется согласующий четвертьволновый трансфор- матор, вся прошедшая в КЛТ СВЧ мощность поглощается в жидкость, то

=υ ^P, (4.18)

где

³ Sсρ₃∆Θ

S₃ − площадь поперечного сечения трубы на участке между сечениями 3

и 4, а ∆Θ определяется соотношением (4.17).

Если же в КЛТ используется согласующий четвертьволновый транс-

форматор, модификация жидкости нетепловая, т.е.

^Рпогл

0 , то

^Рпрош^Р,

и эта мощность может быть использована для реализации дополнительного электротермического процесса (установка гибридного типа), то в этом слу- чае


3
G


3
=υ , (4.19)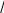

S₃

причем G₃

определяется требуемой производительностью ( м³

с ) КЛТ, а S₃

выбирается такой, чтобы при

υ₃ ,рассчитанной по соотношению(4.18) или

(4.19), на участке между сечениями 3 и 4 течение жидкости было турбу- лентным (см.(4.13)).

В любом случае, принимая во внимание уравнение неразрывности

υ_iS_iυ_kS_k, (4.20)

и

1
где υ_i

и υ_k

− скорость потока в iи kсечениях;

S_iи

S− площади попереч-

k
ного сечения потока в iи kсечениях, скорости
можно представить в виде

υ υ ₆ в сечениях 1 и 6,

�

² υ=υ^�

_�2


₂ S
³ � _,

² υ=²υ�^S

_�2

3 � _,

�
1 3 �_S1 � 6 3 ^�_S6 ^�

□ � � �

и тогда (4.16) с учетом (4.20) можно записать как

�

�

2
gρ^�p�^S3 �
�

−=<sup>�

2</sup> � ₂


^□ υ

�

S
³ � ^{� 3}

�

h−+∆z^�.

1 � � �

^{□ �} 2g^�

�^S6 �

�^S1 � ^�

�

Таким образом, расчет входного давления

nk

p₁ сводится к нахождению h

ni
^h= ∑ ^h+

i=1

∑

j=1

h_mj, (4.21)

где

h_n−_iпутевые потери на преодоление сопротивлений движению жидко-

сти, обусловленных силами трения частиц жидкости друг о друга и о стенки,

ограничивающие поток;

^hmj

− местные потери напора на преодоление мест-

ных сопротивлений, обусловленных различного рода препятствиями в пото-

ке, приводящих к изменению величины или направления скорости течения жидкости; i и j − номера участков путевых потерь напора и местных сопро- тивлений гидравлической системы. Это соотношение не учитывает взаимное влияние местных сопротивлений, но учет этого влияния требует специаль- ных экспериментальных исследований, а потому вслед за [84] при расчетах h будим исходить из суммирования потерь напора по соотношению (4.21).

Рассмотрим гидравлическую систему для нетепловой модификации жидкости, показанную на 4.9. На участке между сечениями 1 и 2 с учетом (4.20) путевые потери напора равны [83]

2 _� ² 2

^λ1^l1 ^υ2

^λ1^l1

S₃ ^� υ₃

h_n1 =

₌ � �

, (4.22)

�

�
d₁ 2g

d₁ ^�S₁ ^� 2g

где λ₁− коэффициент Дарси на участке между сечениями 1 и 2; l₁ и d₁− длина и диаметр гидравлической системы на участке между сечениями 1 и

2; S₁ и S₃ − площади поперечных сечений 1 и 3 трубопровода.

Участок между сечениями 2 и 3 представляет собой местное сопро- тивление − постепенное расширение (расширяющий конус или диффу- зор). Для него

λ ₂n² −1

�n−1�²

h_m1 = ξ<sub>1

υ3</sub>2

2g
, (4.23)

где

₁ ^=ξ _{2 �}⁺� _n� ^sin�;

λ ₂ − коэффициент, учитывающий потери

n8sin₂ ^{� �}

напора на длине

l₂ конуса; n=

^S3 , S

_S2 2

S₁− площадь поперечного сечения 2

трубопровода; − угол между образующими конуса.

Для участка между сечениями 3 и 4 путевые потери напора при υ ₄ υ₃

равны

λ ₃l₃ υ₃²

d
h_n2 =

3

, (4.24)

2g

где

λ₃ − коэффициент Дарси на участке между сечениями 3 и 4;

l₃ и

d₃ −

длина и диаметр трубопровода на участке между сечениями 3 и 4.

Участок между сечениями 4 и 5 представляет собой местное сопротив- ление − постепенное сужение (сужающийся конус или конфузор). Для него
2 _� ² 2

υ₅ S₃ ^� υ₃

^hm2

ξ=_{2 2g}

ξ=₂ <sup>�

□</sup> , (4.25)

2g

�_S5 �

□ �

λ ₄n² −1

где

₂ =ξ

_n2

_�; 8sin ₂

λ₄ − коэффициент, учитывающий потери напора на

длине конуса

S

l₄ ; n= ⁴

S₅
− степень сужение конфузора;
S₄ и
S₅ − площади

поперечных сечений 4 и5 трубопровода; − угол между образующими ко- нуса.

Участок между сечениями 5 и 6 представляет собой местное сопротив-

ление − колено с закруглением. Для него

υ ^{2 �}S^�2 υ ²

= ξh⁶ = ξ<sup>� 3 �

3</sup> , (4.26)

m3 3 _2g

^3�S₆ ^� 2g

^{□ �}d

□ �
_�^3,5 � _δ

где ξ

= ^�0,131+ 0,163^{� 5 � �} ; d− диаметр трубы на участке закругле-

3 ^� �_R� ^� _° ⁵


�

�
_□ � ³ � ⁹⁰

ния;

R₃ − радиус закругления; δ − угол закругления;

S₆ − площадь попереч-

ного сечения трубопровода на участке закругления.

Наконец, в сечении 6 имеется местное сопротивление − внезапное рас- ширение

υ ^{2 �S�2 υ2}

h_m5 = 0,32 ⁶ = 0,32^{� 3 � 3} . (4.27)

2g^�S₆ ^� 2g

□ �

Итак, hпредставляет сумму потерь напора, рассчитываемую по (4.21) с

учетом (4.22) − (4.27), причем все hи hвыражены через

υ₃ и коэффици-

енты Дарси, для расчета которых требуется знать числа Рейнольдса каждого участка гидравлической системы.

При ламинарном режиме в круглых трубах

64

=λ.

Re

Для определения λпри турбулентном режиме к универсальным фор- мулам в первую очередь относят формулу Кольбрука и Уайта, примени- мую для всей области турбулентного течения

1 ^{� К}₁

2,51 ^�

и формулы Альтшуля

2lg^�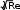


�
^�3,7d

+−=

^�, (4.28)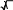

�

�

¹ =1,8lg^Re,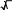

Re^К1 + 7 3,7d

_�К1 _{68 �}0,25

d
λ,= 0,11^�

�

�

₊ �


�
Re^�

где

К₁ − эквивалентная шероховатость стенок трубы [83].

Для гидравлически гладких труб ется формула Прандтля-Никурадзе

^К1 = 0, и из формулы (4.28) получа-

d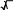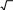

1λ _{= 2lg}Re_,

2,51

а из второй формулы Альтшуля − формула Блазиуса

=R0e,3λ16

0,25 _,

хорошо отвечающая действительности при Re< 10⁵ .

Наконец, для вполне шероховатых труб Re= ∞ применяется формула Прандтля-Никурадзе

λ,= <sup>1

�</sup>1,74 + 2lg^1�2


ε
□ �

□ �

где ε=

^К; К− абсолютная шероховатость труб; − радиус трубы.