Свч электротехнологических установок для модификации диэлектриков

• Название: Свч электротехнологических установок для модификации диэлектриков
• Дата: 01.05.2022
• Размер: 2.15 Mb.
• Имя файла: 1_00676 (1).docx
• Тип: Диссертация; #506934
• страница: 6 из 23

Волноводно-щелевые излучатели обычно собираются на прямо- угольном волноводе с основным типом волны Н ₁₀, когда в широких стенках волновода имеют место поперечные и продольные токи, а на узких стенках

• 
  поперечный ток.
  

Можно говорить о четырех основных типах излучающих щелей (рис.2.11) [54]. Во-первых, продольная щель 1, пересекающая поперечный ток в широкой стенке, если х ₁ ≠ 0. При х ₁ = 0 излучение через узкую щель практически отсутствует. Во-вторых, поперечная щель 2, пересекающая продольный ток в широкой стенке. Излучение через эту щель при х₁ = 0 мак- симально и уменьшается при смещении её от средней линии широкой стен- ке (х₁ ≠ 0). Далее, щель 3, пересекающая как продольные, так и поперечные токи широкой стенки. При х₁ ≠ 0 и δ = 0^◦ щель 3 идентична щели 1, при х₁ = 0, δ = 90^◦ – щели 2. Щель 4 в боковой стенке прямоугольного волновода при δ = 0^◦ практически не излучает, а излучение максимально при δ = 90^◦.

Заметим, что щель 1 при х ₁ = 0 и щель 4 при δ = 0 ^◦ можно использо- вать как практически неизлучающие технологические отверстия, например для ввода или вывода из волновода ленточных модифицируемых объектов или для удаления водяных паров (продувка или вакуумирование) при сушке.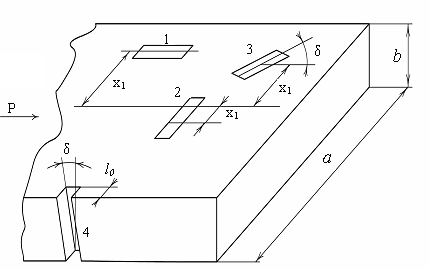


Рис.2.11. Типы излучающих щелей в прямоугольном волноводе

Излучающая щель является нагрузкой для волновода, в которой рас- сеивается часть мощности, эквивалентная мощности излучения, тогда как остальная часть мощности частично отражается, а частично проходит даль- ше по волноводу. Щель можно характеризовать внешней проводимостью излучения [52]

Y_Σ G_Σ jB_Σ ,
где G_Σ , B_Σ − активная и реактивная составляющие проводимости.

Внешняя проводимость излучения резонансной щели, прорезанной в металлическом экране, равна [52]

Y_Σ = G<sub>Σ

=</sub> 0 5R_{Σ ,}

(60π)²

где ^R_Σ − сопротивление излучения эквивалентного симметричного вибрато- ра, но в реальных излучателях со щелями, прорезанными в стенках волно- вода, эта величина всегда меньше на10 – 15 %, то есть [52]

G_Σ.

_≈ 0,45R_Σ

(60π)²

Наряду с внешней проводимостью щель характеризуют внутренней

проводимостью

Y_вн. Знания

^Yвн^{и Y}Σ

позволяют определить резонансную

частоту щели в зависимости от местоположения её на стенке волновода. Обычно в расчетах волновод с основной волной заменяют эквивалентной

двухпроводной линией с параллельно

g+ jb

или последовательно

^jxвключенными сопротивлениями в зависимости от типа щели. При

этом параллельно включенное сопротивление описывает продольную щель, а последовательно включенное сопротивление – поперечную [55].

При расчете волноводно-щелевых излучающих систем обычно поль- зуются последовательным сопротивлением r , нормированным к волновому сопротивлению волновода, и параллельной проводимости g, нормированной

к волновой проводимости волновода. rи gоднозначно связаны с

Y_Σ и могут

быть найдены из условия баланса мощностей в сечении щели волновода. В табл. 2.1 приведены основные типы щелей в стенках волновода, их эквива- лентные схемы и нормированное активные сопротивления и проводимости щелей длиной равной половине длины волны в волноводе (полуволновые щели) [56]. У полуволновых щелей эквивалентная реактивная проводимости b и эквивалентное реактивное сопротивление xравны нулю, а gи r мало меняются вблизи резонанса. Резонансная длина щели несколько мень-

ше ^λи тем меньше, чем шире щель. Резонансная длина щели зависит также

2
от её смещения х₁ относительно оси широкой стенке волновода (рис. 2.12).

Различают также резонансные, нерезонансные волноводно-щелевые излучающие системы с согласованными щелями [56]. Резонансные волно- водно-щелевые излучающие системы представляют собой короткозамкну- тый отрезок волновода с параллельными щелями, расстояние между кото-

рыми равно

λ_вдля щелей, синфазно связанных с полем волновода

(рис. 2.13 а) или 0,5λ_в

• 
  для переменнофазно связанных щелей (рис.2.13 б).
  

Таблица 2.1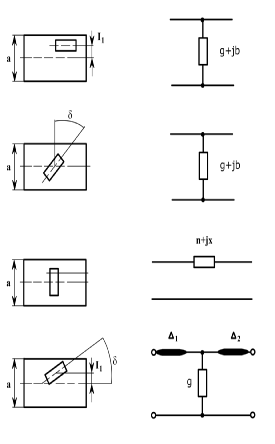

Основные типы щелей, прорезаемых в волноводах, их эквивалентные схемы, и соотношения для эквивалентных нормированных активных сопротивлений и проводимостей полуволновых щелей в прямоугольном волноводе

Расположение щели Экв		ивалентная схема		Эквивалентная проводимость
					g= 2,09 aλвcos2 �π λ � i�πx1 � □ �+ � � bλ �2 λв� � a� □ �π λ � �sin δcos� sin δ� 30 λ λ4 � �2 λв� g= в� � � 73π λ a3b� �λ �2 � □ 1−� � sin2 δ � □ �λв� � □ � � � �λв2 λ2 2 �π λ � 2 �πx1 � r= 0,523� � cos � �cos � � � �λ � ab�2 2a� � a� g+λ=0,82 (a2 b2 ); = π arctgb1 1 1 1 ∆ − 2a1 ∆2 = ∆1 Определение величин а1 и b1 см. [57]. λ − длина волны СВЧ генератора, λв− длина волны волновода, а×b− сечение прямоугольного волновода

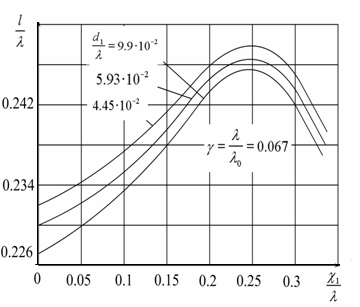Рис. 2.12. К определению резонансной длины продольной щели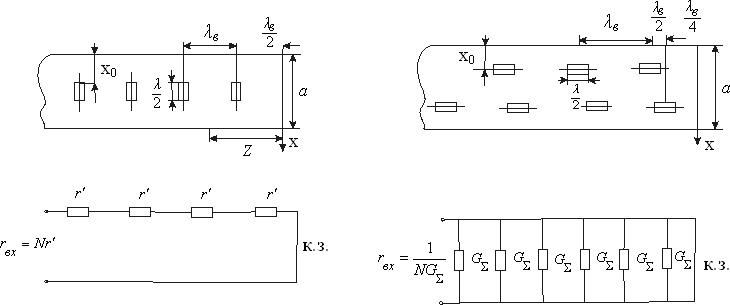



аб
Рис.2.13. Короткозамкнутые волноводы с щелями на широкой стенке и их эквивалентные схемы замещения; а − щели, синфазно связанные с полем волновода; б − переменнофазно связанные щели.
Нерезонансные волноводно-щелевые излучающие системы имеют на конце согласованную нагрузку. Щели располагаются друг от друга на рас-

стоянии d,несколько отличном от 0,5λ_в

λ_в).

(для поперечных щелей отличных от

Обычно КПД по излучаемой мощности таких излучателей составляет 80 – 90 %, так что в КЛТ выгодно использовать резонансные волноводно- щелевые излучающие системы, так как КПД у них выше при равномерном излучении по всей длине излучателя.

Резонансные волноводно-щелевые излучатели для КЛТ могут быть рассчитаны по следующему алгоритму:

1. 
   Определяют геометрические размеры модифицируемого объекта.
   
2. 
   Выбирают частоту СВЧ генератора и соответственно размеры широкой стенки линии передачи с учетом сделанных выше замечаний на этот счет.
   

3. 
   По соотношению b
   

λ_вили l= 0,5λ_ввыбирают длину резонанс-

ной щели, где λ_в– длина волны в волноводе.

4. 
   Определяют ширину щели в излучателе по соотношению.
   

U

(÷2≥,d3) ^m

E_m

где

E_m− предельное значение напряженности электрического поля, при

котором наступает электрический пробой (для воздуха в нормальных атмо-

сферных условиях

Е_пр=30 кВ/см);
U_m= ,

здесь Р−подводимая к антенне мощность,
щели, N−число щелей (обычно N= 15 − 20).

G_Σ − проводимость излучения

5. 
   Задаются длиной волноводно-щелевого излучателя (количество щелей обычно 15 − 20).
   
6. 
   Определяют размеры пятна на поверхности обрабатываемого объ- екта (длина пятна равна длине излучателя, ширина – ширине излучателя).
   
7. 
   Если пятно не закрывает весь объект, то рассчитывают число и расположение дополнительных волноводно-щелевых излучателей.
   

Электромагнитное поле. Обычно для уменьшения габаритов КЛТ модифицируемый объект размещают в ближней зоне излучателя. Как из- вестно, нахождение электромагнитного поля в этой зоне – самостоятельная сложная электродинамическая задача, а потому при расчетах КЛТ обычно ограничиваются рассмотрением простейшего типа электромагнитной волны, когда в каждый момент времени векторы Е и Н электромагнитного поля расположены в плоскости, перпендикулярной направлению движения вол- ны, то есть волна является плоской [6,8,50,57,58] .

Плоская электромагнитная волна описывается следующими диффе- ренциальными уравнениями[59]

dE_х=

dz
μНjω_у,

или

dH_у

dz
jωε=E,_х

d²E_x

dz²
d²Н_у

−= ² Eω_x,εμ


(2.12)

dz²

−ω= ²εμН_у.

Решение уравнений (2.12) имеет вид

Е_х= Е_пр

+ Е_обр=

jγz_+АAеe− jγz_,


2

1
(2.13)

+ Н−_у== Н_пр
^Нобр

^Епр

Z₀

^Еобр_,

Z₀

где при μ

1, Z₀

= ³–⁷х⁷арактеристическое сопротивление среды, в кото-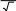

ε

рой распространяется плоская волна=;j+

γ= β

αεµω– постоянная рас-

пространения в среде, Е_пр и Н_пр, Е_обр и Н_обр, А₁ и А₂ – напряженности и амплитуды (приz = 0) прямой и обратной волны, причем

_α= 2π

λ

2π

1 �


2

′
�

�

_′ 1 �

² −+11^�ε,δtg


�
�

₂ �

(2.14)

β= _λ

� + 1εδtg+1�.


2
□ �

Если плоская волна падает на модифицируемый диэлектрик под уг-

лом 90^◦, то коэффициент отражения от поверхности этого диэлектрика равен

Г=,<sup>Z02

Z</sup>01
(2.15)

где цей.
^Z01,2

^Z02 ^{+ Z}01

• 
  характеристические сопротивления диэлектриков с общей грани-
  

Пусть электромагнитная волна падает на границу раздела диэлектри- ков под углом φ ≠ 90^◦ (рис. 2.14). В этом случае коэффициент отражения Г зависит от поляризации падающей волны относительно плоскости падения

[59] .



аб
Рис. 2.14. Схема наклонного падения плоской электромагнитной волны на границу раз- дела воздух-среда: а − перпендикулярная поляризация; б − параллельная поляризация

Если вектор Еперпендикулярен плоскости падения (рис.2.14), то

есть при перпендикулярной поляризации, то коэффициент отражения рас- считывается по соотношению

_Г= Z₀₂ cos

Z₀₁cos

. (2.16)

Z₀₂ cos Z₀ cos�+�

где − угол преломления, причем по второму закону Снеллиуса [59]

_,где_,
^k1⁼,2

k₁sin

k₂ sin

, (2.17)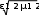

Если вектор Е параллелен плоскости падения (рис. 2.14 б), то есть при параллельной поляризации, то коэффициент отражения рассчитывается по соотношению

_Г= Z₀₂ cos

– Z₀₁cos

. (2.18)

Z₀₂ cos Z₀₁ cos�+�

Если

ε₂ >> ε₁ , то электромагнитная волна при любом угле падения на

границу раздела воздух-диэлектрик в модифицируемом диэлектрике распро- страняется практически по нормали к границе их раздела, при этом каса-

тельные составляющие напряженностей Еи Нв диэлектрике с
приближенным граничным условием Леонтовича [59]

ε₁связаны

^Е1t

Z_nН_1t,

где

Z_n− поверхностный импеданс ( Z_n= Z₀ , если диэлектрик занимает по-

лупространство).

В то же время КПД по использованию СВЧ энергии в КЛТ равен

1Г−=η², (2.19)

а мощность, прошедшая в модифицируемый диэлектрик

^Рпрош

ηР, (2.20)

где Р– мощность, падающая на поверхность обрабатываемого объекта.

Из соотношений (2.13) − (2.19) следует, что КПД является функцией

не только физических параметров диэлектрика, но и угла падения (рис.2.15).

При наличии поглощения в модифицируемом диэлектрике соглас-

но соотношению (2.17) появляются комплексные значения тригонометриче- ских функций. Их аргументы при этом уже не могут иметь наглядного смысла углов ориентации электромагнитной волны. Однако, как отмечается в [59], окончательные результаты расчетов сохраняют свою справедливость и за пределами наглядности, поскольку для этих электромагнитных полей выполняются граничные условия.

Результаты расчета КПД по использованию СВЧ энергии в КЛТ по соотношению (2.19) с учетом (2.16) − (2.18) приведены на рис.2.15. Максимальный КПД, то есть максимальное прохождение электро- магнитной волны в модифицируемый диэлектрик, при перпендикулярной поляризации волны наблюдается при нормальном падении электромагнит- ной волны на его поверхность (φ= 0). Если падающая электромагнитная

волна имеет параллельную поляризацию, то существует угол падения

^�Бр

(угол Брюстера), при котором отражения от границы раздела диэлектриков нет, и падающая электромагнитная волна проникает в модифицируемый ди-

электрик, при этом Ги η0 = 1, причем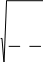


□ _µε�

^□ 1 ₋ 2 ^�

□ _µε�

�
�=arcsin^�

2 1 ^�_.

Бр�

�

�

�

�

^ε1 ₋ ^ε2 �


�

�
ε₂ ε₁ ^�

В случае

µ₁ µ₂

выражение для угла Брюстера имеет вид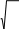

_ε � _ε �

_Бр=�arcsin

² =arctg^�

2 ^�_.

ε+ε

1 2

□ _ε �


1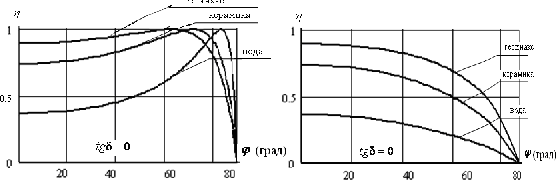
□ �

аб



вг
Рис. 2.15. Зависимость коэффициента полезного действия от угла падения электромаг- нитной волны: а, в – параллельная поляризация; б, г – перпендикулярная поляризация
Важно отметить, что при нормальном падении электромагнитной

волны на границу раздела диэлектриков (φ = 0) величина η не зависит от ви- да поляризации и определяется исключительно диэлектрическими свойства- ми соприкасающихся диэлектриков. Так, согласно рис. 2.15 в случае воды, оптически плотной среды, КПД 40 %, а при оптически менее плотной сре- де (гетинакс) КПД 75 %. При этом отраженная от поверхности модифици-

руемого диэлектрика СВЧ энергия принимается излучающим рупором и по- ступает в СВЧ генератор, отчего в результате перегрева катода магнетрона генератор может выйти из строя. У современных СВЧ генераторов (магне- тронов) допустимый коэффициент стоячей волны по напряжению нагрузки

К_стu > 3, η> 75 %.

3. Технологические процессы, реализуемые в установках с камерами лучевого типа

При проектировании СВЧ электротехнологических установок и их рабочих камер необходимо учитывать свойства модифицируемых диэлек- триков и особенности реализуемых в этих установках технологических про- цессов (рис.2.16). При этом, разумеется, стремятся минимизировать число параметров, которые следует учитывать при проектировании рабочей каме- ры и установки в целом.

Обычно ограничиваются учетом электрофизических (диэлектриче-

ских) и теплофизических параметров модифицируемого диэлектрика: зави-
симости ^ε′ , ^tgδ, удельной теплоемкости с,плотности ρ, коэффициента теп-
лопроводности λ от температуры, а в случае сушки − от температуры и вла- госодержания.В технологических процессах, сопровождающихся термиче- скими напряжениями и разрушениями диэлектрика, задаются также термо- механическими параметрами процесса.

На рис. 2.16 приведены наиболее известные электротехнологические процессы, реализуемые с использованием СВЧ электромагнитных колеба- ний.



Рис. 2.16. Классификация электротехнологических процессов с использованием энергии СВЧ электромагнитных колебаний
Разумеется, наиболее изученными являются тепловые (электротер- мические) модифицирующие процессы обработки диэлектриков. Среди не- тепловых модифицирующих процессов на рис. 2.16 указаны те, о которых имеются сведения. При этом в таких процессах, как модификация синтети- ческих нитей и тканей на их основе, из-за низкого tgδдиэлектриков замет-

ного нагрева волокнистых материалов не наблюдается даже при длительном нахождении диэлектриков в электромагнитном поле большой мощности.

У полимерных смол tgδсущественно больше. Они нагреваются даже при сравнительно коротком пребывании в СВЧ электромагнитном поле.

Отметим, что один и тот же процесс, например пастеризация и сте-

рилизация, может быть как электротермическим, так и нетепловым. В пер- вом случае модифицируемый диэлектрик, твердый, сыпучий или жидкий, нагревается в СВЧ рабочей камере до температуры пастеризации или стери- лизации, при которой подавляются микроорганизмы и споры при теплотех- ническом способе нагрева. Но процесс стерилизации и пастеризации в СВЧ электромагнитном поле можно осуществлять при существенно меньшей температуре и без выдержки [13]. В этом случае эффект пастеризации и сте- рилизации, сопровождаясь определенным нагревом среды, по своей сути яв- ляется нетепловой модификацией.

Наконец, отметим также, что все показанные на рис.2.16 технологи- ческого процесса можно реализовать в СВЧ электротермических установках и в СВЧ электротехнологических установках нетеплового действия на базе КЛТ. Это даёт основание говорить о построении общей теории таких рабо- чих камер.

4. Камеры лучевого типа

с несколькими излучающими системами
Для увеличения поверхности и объема модифицируемого диэлектрика следует использовать несколько излучающих систем (рис. 2.17).

Рис. 2.17 а, виллюстрирует компоновку излучателей, позволяющих модифицировать диэлектрик с большой поверхностью, а рис. 2.17 б, г– с большой поверхностью и объемом.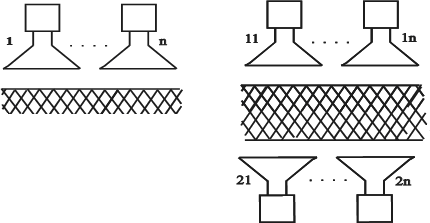


аб


вг
Рис. 2.17. Компоновка нескольких излучающих систем в КЛТ: а, б– камеры с некоге- рентными генераторами; в, г – камеры с когерентными генераторами
Если каждый излучатель получает энергию от отдельного СВЧ генера- тора, то такие КЛТ являются рабочими камерами с некогерентными источ- никами энергии. В каждом элементарном объеме (элементарном слое) мо- дифицируемого диэлектрика мощности СВЧ от разных источников энергии в этом случае складываются. Если же четное количество излучателей с по- мощью делителей СВЧ мощности, отрезков прямоугольных волноводов и поворотов соединены с одним СВЧ генератором, то такие КЛТ являются ра- бочими камерами с когерентными источниками СВЧ энергии. В этом случае при расчете мощности СВЧ в каком-либо объеме (слое) модифицируемого

диэлектрика следует учитывать не только амплитудные, но и фазовые харак- теристики электромагнитных волн, приходящих от разных излучателей.

Наиболее распространенным является применение некогерентных

СВЧ генераторов. При выходе из строя одного из некогерентных генерато- ров его дешевле заменить на аналогичный, чем в случае применения мощно- го СВЧ генератора, который с помощью делителя мощности создает коге- рентные электромагнитные СВЧ колебания в соседних излучающих системах.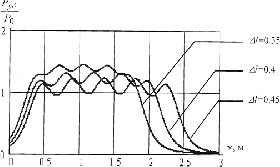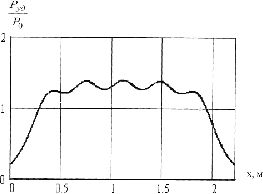




аб

Рис.2.18 Распределения относительной удельной мощности в КЛТ с пятью рупорами: а – при различных расстояниях между рупорами ∆l; б – при оптимальном расстоянии между рупорами (∆l = 0,37 м)
В любом случае в многогенераторных схемах стоит вопрос о равно- мерности распределения в диэлектрике удельной мощности (напряженно- сти) в зависимости от расстояния между излучающими системами. Этот во- прос впервые сформулирован в работе [50]. На рис. 2.18 а, б приведено рас- пределение относительной удельной мощности в КЛТ с пятью излучающи- ми системами при различном расстоянии между ними. Если считать, что распределение плотности СВЧ мощности (напряженности) по всей облу- чаемой поверхности диэлектрика постоянное, то в таком случае излучаю- щие системы должны размещаться без какого-либо зазора между ними в раскрывах излучателей.