Свч электротехнологических установок для модификации диэлектриков

• Название: Свч электротехнологических установок для модификации диэлектриков
• Дата: 01.05.2022
• Размер: 2.15 Mb.
• Имя файла: 1_00676 (1).docx
• Тип: Диссертация; #506934
• страница: 8 из 23

Самосогласованная краевая задача электродинамики и тепломассопереноса

для камер лучевого типа

1. Постановкасамосогласованнойкраевойзадачи

Задача проектирования СВЧ установок тепловой модификации ди- электриков имеет комплексный характер и находится на стыке электроди- намики СВЧ, тепломассопереноса, материаловедения, метрологии, кон- кретной технологии. Процессы в таких установках описываются системой уравнений Максвелла и тепломассопереноса. Исключая из рассмотрения термообработку небольшого класса веществ, у которых электрофизические параметры зависят от векторов напряженности электрического Е и магнит- ного Н полей уже в сравнительно слабых полях (ферромагнетики и сегне- тоэлектрики), можно ограничиться линейной зависимостью вектора элек- трической индукции Dот Еи вектора магнитной индукции Вот Н, а так как подвергаемые СВЧ тепловой модификации среды обычно изотропны, запишем материальные уравнения в виде [10]

DEj

EВμН,

(3.28)

где ε,µ–абсолютные диэлектрическая и магнитная проницаемости среды;

σ– проводимость среды; j–плотность тока проводимости.

Тепловая модификация объектов обычно сводится к нагреву (сушке), а модифицируемые объекты можно отнести к несовершенным диэлектрикам (диэлектрики с потерями), обладающим начальной (структурной) неодно- родностью. Обычно структурные неоднородности многочисленны, размеры их много меньше длины волны в среде, а потому в практических приложе-

ниях, воспользовавшись теорией смесей [65, 66], заменим неоднородную среду однородной с эквивалентными электрофизическими параметрами.

У большинства сред имеются зависимости ε′иtgδот температуры.

Следовательно, при нагреве (сушки) таких сред эти параметры оказываются функциями координат и времени.

Что касается теплофизических параметров, входящих в уравнения и граничные условия задачи о тепломассопереносе, то вслед за [67] примем традиционное для тепловых расчетов допущение о постоянстве этих пара- метров в узком интервале температур (или времени), вводя в рассмотрение их средние на этом интервале значения.

В таком случае уравнения Максвелла и тепломассопереноса в отсутст- вие сторонних токов и объемных зарядов для капиллярно-пористого мате- риала можно представить в виде [6, 10, 68]

rotH= j+ ^∂D, (3.29)

∂t

rotE= j+ ^∂B, (3.30)

∂t

divD

divB

0 , (3.31)

0 , (3.32)

∂Θ _υ

∂t

^k11 2

k₁₂ ²U
^k13

P


₂ уд
p+�+

cρ
�,=+Θ+ (3.33)

∂U_υU

∂t

^k21 2

k₂₂ ²U

^k23

�²+�p�+,=Θ�+
(3.34)

∂ p_υp

∂t

^k31 2

k₃₂ ²U

^k33

�²+�p�,+=Θ�+
(3.35)

где Θ Т

Т₀ ; Т,

a_д, Uи р− температура, коэффициент температуропро-

водности, влагосодержание и давление водяных паров модифицируемого

объекта:
Т₀ – температура окружающей среды;
^k11

= a_д

+ а_m

δε_u;

^k12

ε

= a_m^u;

^k13

ε

= a_pc_p^u;

k₂₁ =
_mδ;

^k22

_m; k₂₃ =

pp^;

k−a=

δε_{u; k}
−a=

^u; ka
ε –скорость транспортиров-

31 m_cp32

m_cp33

p pu

ки модифицированного объекта; _m– коэффициент диффузии влаги; δ –от-

носительный коэффициент термодиффузии;

ε_u– критерий фазового пре-

вращения; _p – коэффициент конвективной фильтрационной диффузии; _p– емкость капиллярно-пористого тела по отношению к влажному воздуху в процессе молярного движения парогазовой смеси; r– удельная теплота па- рообразования; с, ρ − удельная теплоемкость и плотность модифицируемого объекта;

=0,5 ;

′

0уд

Еωδ²Pεtgε

(3.36)

– круговая частота; ₀– абсолютная диэлектрическая проницаемость ва- куума.

Электромагнитные поля в отдельных областях рабочей камеры сопря-

гаются на поверхностях раздела сред1 и2 с помощью граничных условий

[HHn] 0 [n,E− E0

1

2
( 1 ) ( 2 )

(3.37)

nD₂ D₁ 0, nB₂ B₁ =−0=,−

где n– единичный вектор, направленный из среды 2 в среду 1.

Если среда 1 является идеальным проводником, то

[ E]

0, nB

0 . (3.38)

Взаимодействие поверхности модифицируемого объекта с окружаю- щей средой при обмене массой вещества описывается граничными условия- ми четырех видов [68]. Граничные условия первого рода соответствуют слу- чаю, когда потенциал массопереноса на поверхности тела равен потенциалу массопереноса в окружающей среде. В граничных условиях второго рода за-

]
дается поток массы вещества как функция времени. Наиболее часто в при- кладных задачах используются граничные условия третьего рода

λ_д(�Θ)_n

j_n(t) _n

j(t) 0;


m
n

^�( Θ)_nδ

( )_n

( )_nUλ^�+�[jδ+p�(t)+]�= 0;
(3.39)

m_� Θ

p_n= 0,

^p_� ^mn

где

λ_д,

λ_m- коэффициенты теплопроводности и массопроводности модифи-

цируемого объекта, δ_p– коэффициент фильтрационного переноса влаги; δ_Θ

= δ/c_m; c_m– удельная теплоемкость; j_д=hΘ – количество теплоты, отдавае-

мого с поверхности диэлектрика за счет конвекции ; j_m=h_mΘ – плотность потока влаги, отводимой от поверхности диэлектрика (интенсивность испа- рения); h, h_m – коэффициенты теплоотдачи конвекцией и массопереносом.

Наконец, граничные условия четвертого рода характеризуют молеку-

лярный обмен между двумя средами.

При тепловой модификации многих диэлектриков (нагрев асфальта, предпосевная обработка почвы, размораживания грунта и т.д.) массоперенос отсутствует или настолько незначителен, что им можно пренебречь. В таком случае уравнения (3.33) – (3.35) сводятся к уравнению теплопроводности

∂Θ _υ

^Руд


2
а

∂t^д

�+=Θ+

сρ

, (3.40)

В этом случае граничным условием первого рода задано распределе- ние температурного напора по поверхности тела

Θ(t)

Θ₀(t) , (3.41)

граничным условием второго рода задается плотность теплового потока для каждого элемента поверхности тела как функция времени, то есть

^{∂ Θ} = f (τ) , (3.42)

∂ n

(простейший случай

^{∂ Θ} = const), граничным условием третьего рода за-

∂ n

дан закон теплообмена между поверхностью тела и окружающей средой

∂ Θ


∂nλ

h

−= Θ

д
(3.43)

и, наконец, граничным условием четвертого рода − закон теплообмена на соприкасающихся твердых поверхностях

где Θ_1,2=T_1,2 –T₀.

₁ Θ=₂ ,Θ

^∂Θ1 = ^∂Θ2 , (3.44)

∂n∂n

Если в процессе модификации объекта в нем возникают термомехани- ческие напряжения, то для описания процесса к уравнениям электродинами- ки и тепломассопереноса необходимо добавить уравнения термомеханики [8], а при решении задачи технико-экономической оптимизации установки – условие нахождения максимума экономической эффективности установки [9].

2. Методырешениясамосогласованнойкраевойзадачи

Процессы тепловой модификации диэлектрика в СВЧ электромагнит- ном поле могут быть описаны решением краевых задач тепломассопереноса (3.33) −(3.35) и (3.39) и теплопроводности (3.40) и (3.41) – (3.44) в прибли- жении заданного электромагнитного поля, в свою очередь найденного из решения краевой задачи электродинамики (3.29) – (3.32) и (3.37) и (3.38) с учетом (3.36) и (3.28) . Определив, например, экспериментально зависимо- сти электрофизических и теплофизических параметров нагреваемой среды от температуры и влагосодержании при сушке, разобьем время термообра- ботки на интервалы τ, в пределах которых эти параметры будем считать не-

зависимыми от времени. Решение краевой задачи (3.29) – (3.33), (3.37), (3.38) на этом временном интервале определит функцию P_уд(см.(3.36)), что позволяет в явном виде найти решение краевых задач тепломассопереноса

(3.33) − (3.35), (3.39)) или теплопроводности (3.40), (3.41) – (3.44). Решение

краевых задач тепломассопереноса или теплопроводности дает возможность установить электрофизические параметры диэлектрика на следующем вре- менном интервале. Повторяя расчеты для все новых интервалов времени до достижения заданной или установившейся температуры и влагосодержания модифицируемого объекта, можно выяснить динамику процесса, учесть из- менение во времени электрофизических и теплофизических параметров ди- электрика, исследовать влияние различных параметров установки и КЛТ на его характеристики, проводить машинный синтез оптимальных СВЧ элек- тротермических установок.

Поскольку конструкции и режимы работы рабочих камер тепловой модификации существенно различаются, решения краевых задач электроди- намики должны быть проведены для каждого из типов рабочих камер от- дельно. На рис.3.5 и 3.6 показаны блок-схемы решений краевых задач элек- тродинамики и тепломассопереноса, электродинамики и теплопроводности и их место в расчете КЛТ.

Метод решение краевых задач, входящих в самосогласованную крае- вую задачу для КЛТ, выбирается с учетом цели решения. Если речь идет о предварительном расчете рабочей камеры на стадии выбора варианта, выяс- нения общих закономерностей, то целесообразно воспользоваться упро- щенными уравнениями задачи, а если необходимы расчет КЛТ с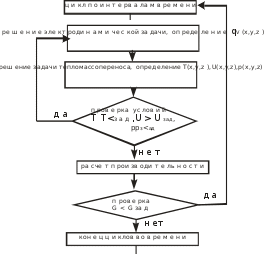











Рис.3.5. Блок-схема решения самосогласованной задачи электродинамики и тепломассо- переноса для расчета КЛТ и математического моделирования процесса тепломассопере- носа.





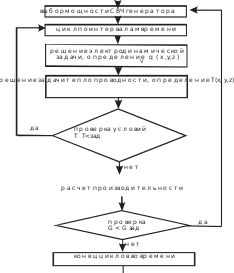Рис.3.6. Блок-схема алгоритма решения самосогласованной задачи электродинамики и теплопроводности для расчета КЛТ и математического моделирования процесса термо- обработки

оптимизацией ее геометрии, выбор параметров и режимов ее работы с целью обеспечения заданных технических параметров и максимальной эффектив- ности установки, то необходимо максимально строгое решение самосогла- сованной краевой задачи. Отметим, при инженерных расчетах обычно ограничиваются первым из этих случаев.

Наиболее распространенными методами решения указанных задач яв- ляются следующие:

• 
  аналитические (решение одномерных уравнений и решение уравне- ний методом разделения переменных);
  
• 
  численные (конечных элементов, конечных разностей);
  
• 
  схем замещения;
  
• 
  комбинированные (численные и схем замещения);
  
• 
  физическое моделирование (натурные устройства, планирование экс- перимента, теория подобия);
  
• 
  аналоговое моделирование (непрерывные среды, сеточные модели, аналоговые вычислительные машины).
  

Аналогичные методы наиболее широко используются в инженерной практике при решении одномерных уравнений для геометрически простых систем и при решении двух- и трехмерных уравнений.

Широкое распространение получили численные методы. Они позво- ляют провести расчет КЛТ любой конфигурации и при любых параметрах модифицируемого объекта.

Наиболее популярен среди инженеров метод схем замещения (эквива- лентных схем) [69 − 72]. Этот метод основан на аппроксимации систем с не- прерывно распределенными параметрами многозвенной цепью определен- ной структуры. Метод схем замещения позволяет определить только токи,

напряжения, сопротивления, мощности, т.е. интегральные параметры. Его точность зависит от достоверности соотношений для расчета элементов схе- мы замещения. Применительно к расчету СВЧ электротермических устано- вок метод эквивалентных схем впервые были использован при расчете КБВ [6, 12].

Характерной тенденцией в области методов решения самосогласован- ных краевых задач электродинамики и теплопроводности (тепломассопере- носа) является создание эффективных комбинированных методов [6, 12].

Если аналоговое моделирование сейчас при проектировании СВЧ электротермических установок практически не используется, то физическое моделирование остается основным методом их создания. Достаточно ска- зать, что только с помощью натурных моделей решаются технологические и конструкционные вопросы.

Таким образом, наибольшее распространение при расчете СВЧ элек- тротермических установок имеют аналитические, численные, комбиниро- ванные методы и метод схем замещения (метод эквивалентных схем).