                 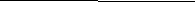       1.Свободные колебания- совершаются без внешних воздействий на счет первоначально полученной телом энергии. (маятник) 1.Свободные колебания- совершаются без внешних воздействий на счет первоначально полученной телом энергии. (маятник)
Колебательный процесс – периодический или почти периодический процесс, который повторяется через одинаковые или почти одинаковые промежутки времени.
Периодические колебания-колебания, при которых значения параметров колебательной системы, меняющейся во времени, в точности повторяются, через равные промеж. времени. (Маятник, каждое его последующее колебание в точности повторяет предыдущее) T- период колебания. n- число полных колебаний в ед. времени n=1/T;
Гармонические колебания- это колебания, при которых колеблющаяся величина изменяется со временем, подчиняющиеся закону синуса или косинуса. X= A cos (ω0t + φ0) А- амплитуда; φ0 начальная фаза колебаний t=0 ; ω0- круговая частота .
Механическое колебательное движение- это повторяющееся движение , при котором тело многократно проходит одно и тоже положение в пространстве.
Пружинный маятник- груз, массой m, подвешенный на упругой пружине и совершающий упругие движения под упругой силой .
Квазиупругая сила – сила, неупругая по природе, но аналогичная по свойствам силам, возникающим при малых деформациях упругих тел .
Дифференциальное уравнение колебаний и его решение – уравнение , связывающее значение производной функции с самой функцией, числами ,значениями переменной . пример( ур. Гармонич колебания)
Характеристика колебаний:
Амплитуда - А(м) — максимальное отклонение колеблющейся величины от некоторого усреднённого её значения для системы.
Промежуток времени Т(сек), через который повторяются какие-либо показатели состояния системы (система совершает одно полное колебание), называют периодом колебаний.
Число колебаний в единицу времени называется частотой колебаний f(Гц, сек-1).
Период колебаний T и частота f — обратные величины;
T=1/f и f=1/T
В круговых или циклических процессах вместо характеристики «частота» используется понятие круговая или циклическая частота w (Гц, сек-1, об/сек), показывающая число колебаний за время 2π:
w=2 π/T=2 π*f
Фаза колебаний — определяет смещение в любой момент времени, то есть определяет состояние колебательной системы.
Скорость и ускорение колеблющейся точки –
Скорость- первая производная от смещения точки по времени v=dx/dt
Ускорение – это вторая производная от смещения точки по времени a=dv/dt
23 Вращение плоскости поляризации. Оптически активные вещества. Поляриметрия.
Вращение плоскости поляризации заключается в повороте плоскости поляризации плоскополяризованного света при прохождении через вещество. Вещества, обладающие таким свойством называют оптически активными. При взаимно перпендикулярных плоскостях свет до наблюдателя не дойдет , так как анализатор не пропустит плоскополяризованный свет в соответствии с законом Малюса.
Если же поместить между поляризатором и анализатором поместить кварцевую пластинку. Так чтобы свет проходил вдоль её оптической оси , то в общем случае свет дойдет до наблюдателя, но если же анализатор повернуть на опр угол , то можно вновь добиться затемнения. Это свидетельствует о том. Что кварцевая пластинка вызвала поворот плоскости поляризации на угол, соответствующий повороту анализатора для получения затемнения, используя в опыте свет различных волн, можно обнаружить дисперсию плоскости поляризации , те зависимость угла поворота от длины волны. Для определения длины волны используют угол α= α₀l. α₀ - коэффициент пропорциональности или постоянная вращения. Оптически активными так же являются многие не кристаллические тела : чистые жидкости(скипидар), растворы оптически активных веществ в неактивных растворителях(сахара), некоторые газы и пары(камфора). α= [α₀]CL. [α₀] – удельное вращение. Это соотношение лежит в основе метода измерения концентрации растворенных веществ, в частности сахара. Поляриметрия или сахариметрия.
26 Разрешающая способность микроскопа.
Предел разрешения – это такое наименьшее расстояние двумя точками предмета, когда эти точки разлчимы, те воспринимаются как две точки. Разрешающей способностью обычно называют способность микроскопа давать раздельные изображения мелких деталей рассматриваемого предмета. Микроскоп - это оптический прибор, позволяющий получить обратное изображение изучаемого объекта и рассмотреть мелкие детали его строения, размеры которых лежат за пределами разрешающей способности глаза.
Разрешающая способность микроскопа дает раздельное изображение двух близких друг другу линий. Невооруженный человеческий глаз имеет разрешающую способность около 1/10 мм или 100 мкм. Лучший световой микроскоп примерно в 500 раз улучшает возможность человеческого глаза, т. е. его разрешающая способность составляет около 0,2 мкм или 200 нм.
2. Энергия колебания. Зависимость энергии от амплитуды.
Свободные механические колебания. (незатухающие и затухающие).
Свободными(собственными) колебаниями называют такие, которые совершаются без внешних воздействий за счет первоначально полученной телом энергии. Характерными моделями таких механических колебаний являются материальная точка на пружине (пружинный маятник) и материальная точка на нерастяжимой нити (математический маятник).
F= -kx, где k – коэффициент пропорциональности между силой и смещением, который в данном случае является жесткостью пружины; знак минус показывает, что сила всегда направлена в сторону положения равновесия. F- упругая сила тяжести (=mg)
Незатухающие колебания(гармоническое колебание). Амплитуда и начальная фаза колебаний определяется начальным условиями движения, т.е. положением и скоростью материальной точки в момент t=0. Среди различных видов колебаний гармоническое колебание является наиболее простой формой. Таким образом, материальная точка, подвешенная на пружине (пружинный маятник) или нити (математический маятник), совершает колебания, если не учитывать силы сопротивления.
Затухающие колебания. В реальном случае на колеблющееся тело действуют силы сопротивления (трения), характер движения изменяется, и колебание становится затухающим.
Также имеется кинетическая и потенциальная энергия, которые вычисляются по формуле:
Eкин=1/2kA²sin²(w₀t+µ₀); Eп= 1/2kA²cos²(w₀t+µ₀)
Складывая кинетическую и потенциальную энергию, получаем полную механическую энергию материальной точки, колеблющейся по гармоническому закону:1/2kA². Если отсутствует силы трения полная полная механическая энергия системы не изменяется: E= 1/2kA²=1/2mw²₀A²
3.Затухающие колебание, их характеристика. Дифференциальное уравнение колебаний, его решение. Коэффициент затухания. Логарифмический декремент затухания.
Затухающее колебание- колебание с постоянно убывающей со временем амплитудой. Затухание обусловлено в основном трением (механические системы) и сопротивлением (в электромагнитных колебательных контурах). Дифференциальное уравнение свободных затухающих затухающих колебаний = второму закону Ньютона.
Учитывая, что а силу сопротивления, которая обычно пропорциональна скорости, можно записать
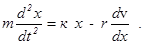
как где r – коэффициент сопротивления, т.е. коэффициент пропорциональности между скоростью и силой сопротивления.
Решение этого уравнения имеет вид:
,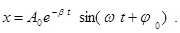
Колебательный процесс может происходить лишь при условии: (w02 - b 2)>0, когда частота w является действительной величиной . Если же затухание в системе слишком велико (w0 < b ) , то под корнем в формуле оказывается отрицательная величина, - в этом случае движение не имеет периодического характера.
Уже указывалось, что быстрота убывания амплитуды затухающих колебаний характеризуется коэффициентом затухания b , который зависит от параметров системы. На практике затухание колебаний удобнее характеризовать декрементом затухания d , представляющим собой отношение двух последовательных амплитуд, разделенных периодом колебаний Т
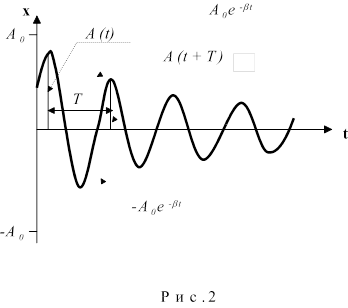
Натуральный логарифм этого отношения, называемый логарифмическим декрементом затухания.
|
21. Электромагнитные волны как поперечные. Плоскость поляризации.Поляризаторы и анализаторы. Закон Малюса.
Волну, в которой направление колебаний светового контура Е упорядочено каким-либо образом, наз-ют поляризованной. Если колебания вектора Е происходит только в одной плоскости, проходящей через луч, то это плоско (линейно) поляризованная волна.
Плоскость. В которой колеблется вектор Е, называют плоскостью поляризации (плоскостью колебаний светового вектора).
Если вектор Е вращается вокруг направления распространения волны одновременно изменяясь периодически по модулю и при этом конец вектора Е описывает эллипс ( в каждой точке среды), то это эллиптически-поляризованная волна (или поляризованной по кругу, если конец вектора описывает окружность).Эллиптически-поляризованная – наиболее общий вид поляризации волны,переходящий при опред-ых условиях в линейную и круговую поляризации. Волну с эллиптической поляризацией можно разложить на 2 перпендикулярные линейно-поляризованные волны с взаимно ортогональными плоскостями поляризации. Разность фаз этих волн сох-ся постоянной.
Естественный свет- световые волны не обнаруживают асимметрии по отншению к направлению распространения. В естест-ом свете колебания вктора Е в любой точке (фиксированной) среды совершаютя в разных направлениях, быстро и беспорядочно сменяя друг друга.Естест-ый свт можно представить как сумму двух некогерентных плоскополярилованных волн с взаимно ортогональными плоскостями поляризации.
Поляризованный свет-свет, получаемый в искусственных условиях при прохождении светового пучка через специальное устройство (поляризатор). Поляриз-ый свет отличается от естетвен-го физическими характеристиками ( ориентированностью световых волн, колебания которых происходит в одной плоскости).
Устройство, позволяющее получать поляризованный свет из естественного наз-ют поляризатором. Эти приборы свободно пропускают колебания светового вектора, параллельные плоскости( плоскость пропускания поляризатора). Поляризатор можно использовать для анализа поляризованного света, тогда его наз-ют анализатором.
Помимо плоскополяризованного и естественного света сущ-ет частично-поляризованный свет. Его можно представить в виде наложения двух некогерентных плоскополяризованных волн с взаимно перпендикулярными плоскостями поляризации.
Закон Малюса. Пусть анализатор падает на линейно-поляризованный свет, вектор Е(0) которого сос тавляет угол φ с плоскостью пропускания Р. Анализатор пропускает только ту составляющую вектора Е(0) , которая параллельна плоскости пропускания Р, т.е Е=Е(0)cosφ Интенсивность пропорциональна квадрату модуля светового вектора, поэтому интенсивность прошедшего света: I=I(0)cos^2φ
Где I(0)- интенсивность падающего плоскополяризованного света. Это соотношение выражает закон МАЛЮСА.
24 Геометрическая оптика как предельный случай волновой оптики. Формула тонкой линзы. Идеальная центрированная оптическая система.
Геометрическая оптика используется там, где волновые свойства света могут не учитываться. Это есть предельный случай волновой оптики при стремлении длины волны к нулю. Это можно рассмотреть на примере дифракционной решетки. так как длина волны стремиться к нулю и альфа стремиться к нулю, получаем обычное для линзы фокусирование параллельного пучка света в точке.
Формула тонкой линзы: 1/a(1) +1/f(2) = (n-1)(1/R(1) =1/R(2), где а (1) - это расстояние от предмета до линзы, а а(2) - расстояние от изображения до линзы, R(1),R(2)- радиусы кривизны передней и задней поверхности сферических поверхностей линзы, n – показатель преломления вещества. Ее так же можно представить в виде 1/f=1/a(1)+1/a(2). Соотношение получено для тонкой линзы при след предположениях: изображение формируется узкими приосевыми пучками, составляющие небольшие углы с главной осью системы; показатель преломления для всех волн одинаков. При данных условиях создается точечное изображение. Но это не всегда выполняется, значит происходит абберации или погрешности реальных оптических систем, приводящим к снижению качества оптических изображений.
Часто используемые на практике системы сферических поверхностей (линз), центры которых лежат на одной прямой – главной оптической оси, называются центрированными:
А) каждой точке или линии пространства предметов соответствует только одна точка или линия пространства изображений(сопряженные точки)
В)оптическая система характеризуется шестью кардинальными точками и шестью кардинальными плоскостями.
Глаз человека является своеобразным оптическим прибором, занимающим в оптике особое место.
|
17. Интерференция света – это явление сложения световых волн, при котором наблюдается устойчивая картина усиления и ослабления интенсивности света. При интерференции происходит перераспределение энергии в пространстве (между max и min). Когерентные (согласованные) источники света Это источники, излучающие волны, разность фаз которых постоянна во времени в различных точках пространства: f (t) const Когерентные волны можно получить путем “расщепления” световой волны, излучаемой от одного источника
Когерентные волны имеют одинаковую частоту
Мax интенсивности при интерференции образуется в тех точках пространства, где оптическая разность хода волн равна целому числу длин волн (четному числу длин полуволн)
cos 1
Imax>(I1+I2)
Min интенсивности при интерференции образуется в тех точках пространства, где оптическая разность хода волн равна нечетному числу длин полуволн
cos -1
Imin<(I1+I2)
18.Интерференция в тонких пленках- Пленка называется тонкой, если ее толщина соизмерима с длиной волны ( света При отражении волны от более плотной среды в точке А фаза волны 1 меняется на противоположную (на ) Это равносильно изменению оптической длины пути на /2 (потере полволны) При интерференции в тонкой пленке происходит перераспределение энергии: падающий поток перераспределяется на отраженный и проходящий
Если в отраженном свете наблюдается max интерференции, то в проходящем свете будет min интерференции (и наоборот) При освещении пленки белым светом она в отраженном свете станет окрашенной
Просветленная оптика - изделия с такими покрытиями
Покрытие оптических поверхностей тонкой пленкой из оксидов металлов Толщину пленки подбирают так, чтобы она соответствовала условия MIN интерференции в отраженном свете (MAX в проходящем) в желто- зеленой части спектра. Это позволяет увеличить долю прошедшего света Просветленная оптика - изделия с такими покрытиями. Интерференционный микроскоп. Позволяет увидеть прозрачные микрообъекты Сочетание интерферометра и микроскопа.
22 поляризация при отражении и преломлении. Закон Брюстера.
При отражении от границ 2х диэлектриков естественный свет частично поляризуется. В отраженном луче преобладают колебания , перпендикулярные плоскости падения, а в преломленном – параллельные ей. Если угол падения удовлетворяет условии tg i(б)=n(21), то отраженный монохроматический свет луч полностью поляризован. Это соотношение выражает закон Брюстера. I(б) – угол брюстера или угол полной поляризации, n(21) =n(2)/n(1) –относительный показатель преломления второй среды относительно первой. Преломленный луч всегда частично поляризован, при чем при падении под углом брюстера степень его поляризации наибольшая. Используя выражение закона брюстера и закон преломления можно показать что при полной поляризации отраженного света угол между преломленным и отраженным лучами равен 90°. Таким образом , граница раздела двух диэлектриков или диэлектрика и вакуума служит поляризатором . независимо от угла падения степень поляризации преломленного луча возрастает по мере прохождения пластин.
8. Отражение и преломление звука. Затухание звука. Формула Рэлея.
Волновое сопротивление – важнейшая характеристика среды, определяющая условия отражения и преломления волн на ее границе. Закон отражения и преломления звуковой волны аналогичны законам отражения и преломления света. Преломленная волна может поглотиться во второй среде, а может выйти из нее. Процесс постепенного затухания звука в закрытых помещениях после выключения источника называется реверберацией. Реверберация с одной стороны полезна, так как восприятие звука усиливается за счет энергии отраженной волны, но, с другой стороны, чрезмерно длительная реверберация может существенно ухудшить восприятие речи. Закон Рэлея — Джинса — закон излучения для равновесной плотности излучения и для испускательной способности абсолютно чёрного тела, который получили Рэлей и Джинс в рамках классической статистики (теорема о равнораспределении энергии по степеням свободы и представление об электромагнитном поле как о бесконечномерной динамической системе)музыки, так как каждая новая часть текста перекрывается предыдущим.
Формула Релея:
4. Вынужденные колебания. Дифференциальное уравнение колебаний и его решение. Резонанс. Резонансная частота.
Вынужденные колебания называются колебания, возникающие в системе при участии силы, изменяющейся по периодическому закону.
Составим Дифференциальное уравнение колебаний: 
Решение данного уравнения имеет вид: 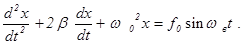
Явление резкого возрастания амплитуды вынужденных колебаний при частоте действия вынуждающей силы, называется резонансом. Определяется по формуле: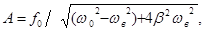
Резонансную круговую частоту можно найти из условия минимума знаменателя:
Механический резонанс может быть как полезным, так и вредным явлением. Вредное действие резонанса связано главным образом с разрушением, которое он может вызвать. Так, в технике, учитывая разные вибрации, необходимо предусматривать возможное возникновение резонансных условий, в противном случае могут быть разрушения и катастрофы. Тела обычно имеют несколько собственных частот и соответственно несколько резонансных частот.
5. Определение волны. Продольные и поперечные волны. Фронт волны. Плоские, сферические и цилиндрические волны. Плоская гармоническая волна. Скорость (фазовая) волны. Уравнение плоской гармонической волны. Характеристики волны. Длина волны.
Механической волной называют механические возмущения, распространяющиеся в пространстве и несущие энергию. Различают два основных вида механических волн: упругие волны (распространение упругих деформаций) и волны на поверхности жидкости. Упругие волны возникают благодаря связям, существующим между частицами среды: перемещение одной частицы от положения равновесия приводит к перемещению соседних частиц. Этот процесс распространяется в пространстве с конечной скоростью.
Уравнение волны выражает зависимость смещения колеблющейся точки (s), участвующей в волновом процессе, от координаты ее равновесного положения и времени. s=f(x,t), если x и s направлены вдоль одной прямой, то волна продольная, если они взаимно перпендикулярны, то волна поперечная. Множество точек, имеющих одновременно одинаковую фазу, называют фронтом волны.
Плоская волна – это волна, имеющая плоский фронт волны. 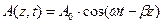
Сферическая волна – это волна, имеющая сферический фронт волны. Уравнение сферической волны имеет вид
Цилиндрическая волна – это волна, имеющая фазовый фронт в виде цилиндрической поверхности. Уравнение цилиндрической волны имеет вид
Плоские электромагнитные гармонические волны, описываемые уравнениями: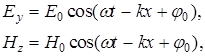 где Е0, Н0 – амплитуды напряженностей электрического и магнитного полей. где Е0, Н0 – амплитуды напряженностей электрического и магнитного полей.
Длиной волны называют расстояние между двумя точками, фазы которых в один и тот же момент времени отличаются на 2π. Она равна расстоянию, пройденному волной за период колебания: µ=Тv
|
19. Определение дифракции. Принцип Гюйгенса-Френеля. Дифракция света – это отклонение света от прямолинейного распространения в среде с резкими неоднородностями. Дифракция света – это огибание световыми волнами препятствий, расположенных на пути распространения волны.
Дифракционная картина - система темных (min) и светлых (max) участков на экране: а) кольца «круглые препятствия» (диск, шарик, отверстие) б) полосы «линейные препятствия» (щель, нить)
Дифракцию можно наблюдать только если размеры препятствия соизмеримы с длиной волны падающего света.
Принцип Гюйгенса-Френеля, позволяет объяснить и рассчитать дифракционную картину.
Гюйгенс: 1. Каждая точка волновой поверхности, которой достигла в данный момент времени волна, является источником (центром) вторичных волн 2. Внешняя огибающая вторичных волн образует фронт волны (волновую поверхность) в следующий момент времени t Френель: 3. Вторичные волны являются когерентными и при их сложении наблюдается интерференция. Дифракционная решетка. Дифракционный спектр.
Дифракционная решетка – это оптическое устройство, представляющее собой совокупность большого числа параллельных щелей. Щели в решетке расположены на одинаковом расстоянии друг от друга
Дифракция Фраунгофера — случай дифракции, при котором дифракционная картина наблюдается на значительном расстоянии от отверстия или преграды.
Разрешающая способность (разрешающая сила) дифракционной решетки – величина, характеризующая способность решетки давать раздельное изображение двух близких спектральных линий ( и ): R =/
-минимальная разность длин волн двух монохроматических линий равной интенсивности, которые еще можно различить в спектре R= kN
k – порядок MAX; N– число щелей решетки
20.Кристалл как трехмерная дифракционная решетка
Основная формула дифракционной решетки применима к измерению параметров кристаллической решетки посредством дифракции рентгеновских лучей.Естественной объемной периодической структурой являются
Кристаллы, крупные молекулы и т.п. Вторичные волны в кристалле возникают в рез-те взаимодействия первичных лучей с электронами атомов. Т.к расстояние между рассеивающими атомами в кристалле приблизительно равны длине волны рентгеновского излучения, кристалл для этих лучей явл-ся трехмерной дифракционной решеткой.
Условие дифракционных максимумов при отражении рентгеновских лучей от кристалла( формула Вульфа-Брэгга)
Формула Брэгга-Вульфа:  – условие максимума при дифракции отражённых рентгеновских лучей на кристалле. – условие максимума при дифракции отражённых рентгеновских лучей на кристалле.
Дифракция на кристалле используется для анализа спектрального состава рентгеновского излучения и ля исследования кристаллов.
Рентгеноструктурный анализ- один из дифракционных методов исследования структуры вещества. В основе данного метода лежит явление дифракции рентгеновских лучей на трехмерной кристаллической решетке. Метод позволяет определять атомную структуру вещества, включающую в себя пространственную группу элементарной ячейки, ее размеры и форму, а также определить группу симметрии кристалла. Этот анализ относительно прост и дешев.
Разновидности метода: Метод Лауэ применяется для монокристаллов. Образец облучается пучком с непрерывным спектром, взаимная ориентация пучка и кристалла не меняется. Угловое распределение дифрагированного излучеия имеет вид отдельных дифракционных пятен.
Метод Дебая-Шеррера используется для исследования поликристаллов и их смесей. Хаотическая ориентация кристаллов в образце относительно падающего монохроматического пучка превращает дифрагированные пучки в семейство коаксинальных конусов с падающим пучком на оси. Их изображение на фотопленке имеет вид концентрических колец.
6. Эффект Доплера и его использование в медицине.
Эффектом Доплера называют изменение частоты волн, воспринимаемых наблюдателем (приемником волн), вследствие относительного движения источника волн и наблюдателя. Эффект Доплера можно использовать для определения скорости движения тела в среде, так же для определения скорости кровотока, скорости движения клапанов и стенок сердца (доплеровская эхокардиография) и других органов.
Разница частот- доплеровский сдвиг частот:
 v₁ v₁
|
 Скачать 132.37 Kb.
Скачать 132.37 Kb.