лабораторная работа 10 по физике 1 курс тулгу. T)Asin(

• Название: T)Asin(
• Анкор: лабораторная работа 10 по физике 1 курс тулгу
• Дата: 30.04.2023
• Размер: 38.02 Kb.
• Имя файла: Dokument_Microsoft_Word_2.docx
• Тип: Закон; #1099079

1. 
   Какие колебания называются гармоническими? При каких необходимых условиях гармонические колебания возникают в механической системе?
   

колебания, при которых физическая величина изменяется с течением времени по гармоническому (синусоидальному, косинусоидальному) закону.

2. 
   
   В каком случае маятник совершает собственные затухающие колебания, и чем они отличаются от незатухающих гармонических колебаний?
   

В случае когда действуют те или иные силы сопротивления (трение в точке подвеса, сопротивление окружающей среды и т.п.), на преодоление которых система затрачивает энергию, вследствие чего реальные свободные механические колебания всегда являются затухающими.

3. 
   
   От каких параметров зависит сила вязкого трения, и в каком случае её надо учитывать?
   

Сила вязкого трения пропорциональна скорости относительного движения V тел, пропорциональна площади S и обратно пропорциональна расстоянию между плоскостями h.

4. 
   
   Какие величины называются коэффициентом вязкого трения и коэффициентом затухания колебаний? Как они вычисляются в работе?
   

Коэффициент вязкого трения представляет собой отношение динамического коэффициента вязкости жидкости к её плотности:



Коэффициент затухания — величина, которой определяется быстрота (скорость) убывания амплитуды.

5. 
   Запишите уравнение движения пружинного маятника и получите с его помощью динамические уравнения собственных незатухающих и затухающих колебаний.
   

X=A*cos(ω₀t+𝜑)=A*sin(ω₀t+𝜑₁)

Затухающие:

Незатухающие:

6. 
   
   Какие величины называются амплитудой, фазой и начальной фазой затухающих и незатухающих собственных колебаний?
   

Амплитуда - максимальное значение смещения маятника.

Фаза колебаний - аргумент периодической функции, описывающей колебательный или волновой процесс.

Начальная фаза колебаний— значение фазы колебаний (полной) в начальный момент времени, то есть при t = 0 (для колебательного процесса)

7. 
   Пружинный маятник с массой m на пружинке с жёсткостью k, совершающий незатухающие гармонические колебания, имеет в начальный момент времени t = 0 координату x₀=x и скорость v₀=v . Чему равна амплитуда и начальная фаза этих колебаний?
   

Для определения амплитуды может использоваться формула: А=√x2+v2/w2. Начальная фаза высчитывается по формуле: tg(f)=-v/xw

8. 
   В каком случае пружинный маятник с массой m и коэффициентом жёсткости k будет совершать в жидкости апериодическое движение, если коэффициент вязкого трения при его движении равен η?
   

Для малых декрементов затухания колебания близки к гармоническим, при больших ϒ затухание происходит за 1—2 периода. В том случае, когда ϒ >=w₀ значение частоты w становится мнимым и гармонические колебания не реализуются, происходит апериодический процесс—тело маятника после начального отклонения плавно возвращается в положение равновесия. Величина ϒ получила название декремента затухания. При этом величина 1/ ϒ равна времени, за которое амплитуда колебаний затухает в е раз.

9. 
   
   Получите формулу периода колебаний пружинного маятника в вязкой жидкости. Как изменяется его величина с ростом вязкости?
   

где А0 и φ0 – начальная амплитуда и начальная фаза колебаний;

B - циклическая частота затухающих колебаний;

где r – постоянная, называемая коэффициентом сопротивления.

10. 
    Какая величина называется логарифмическим декрементом затухания колебаний, как она связана с периодом колебаний и каким образом она вычисляется в данной работе?
    

Логарифми́ческий декреме́нт колеба́ний — безразмерная физическая величина, описывающая уменьшение амплитуды колебательного процесса и равная натуральному логарифму отношения двух последовательных амплитуд колеблющейся величины x в одну и ту же сторону: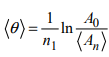

11. 
    Объясните различие методов, используемых в работе при определении коэффициента жёсткости пружины статическим и динамическим способом.
    

Для определения статического коэффициента жёсткости пружины статическим методом необходимо измерить длину , на которую растянется пружина при подвешивании к ней груза известной массы m. Жесткость пружины определяется из условия равновесия груза.

Период собственных колебаний системы и масса груза позволяет вычислить коэффициент жесткости динамическим способом по формуле