кинематический расчет передачи. Рисунок 11 вариант 6 Кинематический и расчет зубчатой передачи. Техническое задание. 1 Исходные данные для проектирования приводов Для задания 11 Варианты 1 2 3

• Название: Техническое задание. 1 Исходные данные для проектирования приводов Для задания 11 Варианты 1 2 3
• Анкор: кинематический расчет передачи
• Дата: 16.03.2022
• Размер: 200.5 Kb.
• Имя файла: Рисунок 11 вариант 6 Кинематический и расчет зубчатой передачи.doc
• Тип: Техническое задание; #399922

1 Техническое задание.

Таблица 1.1 - Исходные данные для проектирования приводов

Для задания 11
Варианты	1	2	3	4	5	6	7	8	9
Мощности потребителей N II вых = N III вых, кВт	5	5	6	6	6	7	7	8	8
Угловые скорости выходных валов  II =  III , рад / c	80	75	70	65	60	55	50	45	40
Требуемый ресурс Lh, тыс. ч	5	6	7	8	9	10	11	12	13

2 Кинематический и силовой расчеты привода.
2.1 Определение КПД кинематических цепей в приводе и выбор электродвигателя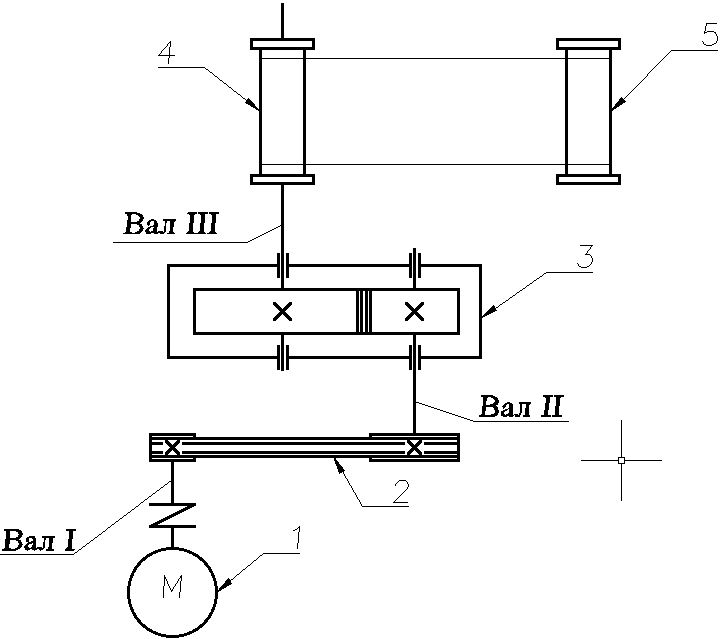



1-электродвигатель; 2-клиноременная передача; 3-редуктор прямозубый; 4-барабан; 5-ролики

Рисунок 2.1
КПД кинематической цепи: двигатель - выходной конец III вала, по которой передается первый поток мощности ( в соответствии с рисунком 21 )

III= рем  цил  ²пк_.= 0,95  0,96  0,99² = 0,894,

где рем - КПД клиноременной открытой передачи 3, С. 21;

цил - КПД цилиндрической прямозубой закрытой передачи 3, С. 20;

пк - КПД подшипников качения с одного вала 3, С. 21.

Требуемая мощность двигателя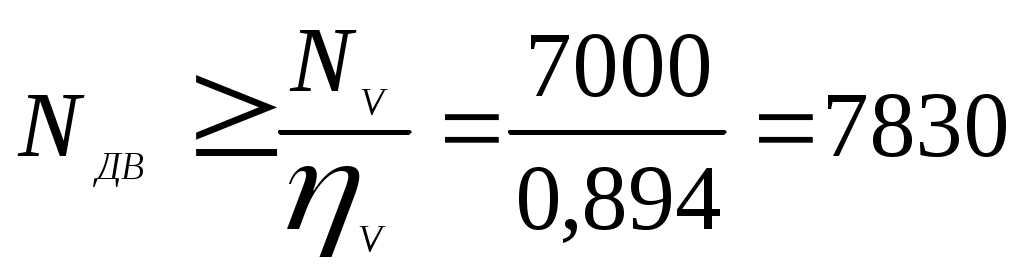

Вт,

где NIII - мощность, потребляемая с выходного конца III вала ;

Ориентировочная угловая скорость вращения вала двигателя _ДВ

_ДВ  _III  i_{1- 2}  i_{2 - 3} = 55*1,39  2,0 = 152,9 рад / с ;

где  _III =  III на 1 скорости - угловая скорость вращения вала III, рад  c.

i_1-2 - передаточное отношение ременной передачи, согласно таблице 4.1;

i_2-3 - передаточное отношение цилиндрической прямозубой передачи, согласно таблице 4.1;

По таблице 4.2 выбираем асинхронный двигатель закрытый обдуваемый серии 4А: электродвигатель 4А142М4 У3 ГОСТ 19523-81  3, С. 24  , мощностью N дв.гост = 11 кВт и синхронной частотой вращения nдв.гост=1500обмин. Величина скольжения s=2,8%=0,028

Асинхронная частота вращения вала двигателя

n дв = n_с (1 - s) = 1500 (1 – 0,028) = 1458,0 об/мин

Асинхронная угловая скорость вращения вала двигателя

рад / с.
2.2 Разбивка общего передаточного отношения привода между

передачами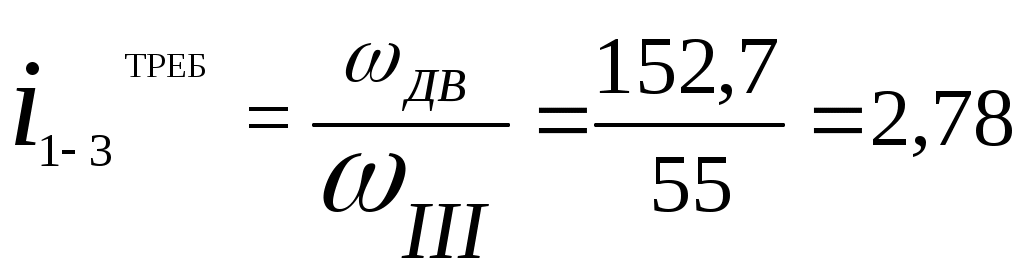

Требуемое общее передаточное отношение передач, через которые передается первый поток мощности на вал III

.

Фактическое значение общего передаточного отношения передач, через которые передается первый поток мощности на вал III

i _{2- 11} ^{ф а к т} = i_{1- 2}  i_{2 - 3} =1,390 *2,0 = 2,78 .

Отклонение передаточного отношения i_1-3^{ф а к т} от i_1-3^{т р е б} составляет 0,0 %  1 % , что приемлемо.


2.3 Определение мощностей, угловых скоростей и вращающих

моментов на валах привода
Мощности на элементах привода

N₁ = N дв = 7830 Вт ;

N₂ = N₁  рем  пк = 7830  0,95 0, 99 = 7364 Вт ;

N₃ = N₂  цил  пк = 7364  0, 96  0, 99 = 6999 Вт ;

Угловые скорости и частоты вращения элементов привода

₁ = дв = 152,7 рад  с ;

2 = ₁  i _1-2 = 152,7  1,39 = 109,9 рад  с ;

 3 = ₂  i _2-3 = 109,9  2,0 = 54,9 рад  с ;

n _I =  _I  9,55 = 152,7  9,55 = 1458,3 об / мин ;

n _II =  _II  9,55 = 109,9  9,55 = 1049,5 об / мин ;

n _III =  _III  9,55 = 54,9  9,55 = 524,3 об / мин ;

Вращающие моменты на элементах привода

Т₁ = Тдв = Nдв   дв = 7830  152,7 = 51,277 Нм ;

Т₂ = Т₁  i _1-2  рем  пк = 51,277  1,39  0,95 0,99 = 67,034 Нм ;

Т₃ = Т₃  i _2-3  цил  пк = 67,034  2,0 0,96  0,99 = 127,419 Нм
Результаты расчетов сведем в таблицу 2.1

Таблица 2.1

Номер вала	Мощность, Вт	Угловая скорость, рад / c	Вращающий момент, Нм	Частота вращения, об/мин
Вал двигателя I вал	Nдв= 7830 N1 = 7830	дв = 152,7 1 = 152,7	Тдв = 51,277 Т1 = 51,277	n ДВ = 1458,3 n 1 = 1458,3
II вал	N2 = 7364	2 = 109,9	Т2= 67,034	n2 = 1049,5
III вал	N3 = 6999	3 = 54,9	Т3 = 127,419	n 3 = 524,3

Расчет закрытой цилиндрической прямозубой передачи
Исходные данные для расчета:

– передаточное число u = 2,0;

– частота вращения шестерни n₁ = 1049,5 мин^-1;

– частота вращения колеса n₂ = 524,3 мин^-1;

– вращающий момент на шестерне Т₁ = 67,034 Н·м.

Число лет работы передачи при трехсменной работе – 5 лет.

Передача нереверсивная, нагрузка постоянная, производство мелкосерийное.
1) Выбор материалов и термической обработки колес

При мелкосерийном производстве и невысоких требованиях к размерам редуктора выбираем материалы:

для шестерни – сталь 45, термообработка – улучшение, твердость 269–302 НВ, средняя твердость НВ₀₁ = 285;

для колеса – сталь 45, термообработка – улучшение, твердость 235–262 НВ, средняя твердость НВ₀₂ = 250.
2) Определение допускаемых контактных напряжений

, МПа,

где σ_Нlim – предел контактной выносливости при базовом числе циклов напряжений N_H0:

для шестерни МПа;

для колеса МПа;

Z_N – коэффициент долговечности;

S_H – коэффициент запаса прочности, S_H = 1,1.

Базовое число циклов напряжений:

для шестерни ;

для колеса .

Расчетное число циклов напряжений за весь срок службы передачи при постоянном режиме нагружения:

,

где n – частота вращения шестерни, колеса, мин^-1;

с – число зацеплений зуба за один оборот колеса. Для нереверсивной передачи с = 1;

L_h – срок службы передачи, ч:

,

где L – число лет работы передачи, L = 5 лет;

К_г – коэффициент годового использования передачи, К_г = 0,85;

К_с – число смен работы передачи в сутки, К_с = 3.

ч

Расчетное число циклов напряжений:

– для шестерни

=60*1049,5*1*37230=234*10⁷

– для колеса

.=60*524,3*1*37230=117*10⁷

Для длительно работающих передач при N_K > N_H0 коэффициент долговечности равен:

.

– для шестерни .

– для колеса

Допустимые контактные напряжения:

– для шестерни =640*0,79/1,1= 460 МПа

– для колеса =570*0,81/1,1= 420 МПа

Расчетное допускаемое контактное напряжение:

=420 МПа

3) Определение допускаемых напряжений изгиба

, МПа,

где σ_Flim – предел выносливости зубьев при изгибе, соответствующий базовому числу циклов напряжений:

– для шестерни МПа;

– для колеса МПа;

S_F – коэффициент запаса прочности, S_F = 1,7;

Y_R – коэффициент, учитывающий влияние шероховатости переходной поверхности между зубьями, Y_R = 1;

Y_Z – коэффициент, учитывающий способ получения заготовки шестерни и колеса. Для поковок и штамповок Y_Z = 1;

Y_А – коэффициент, учитывающий влияние двустороннего приложения нагрузки. При нереверсивной передаче Y_А = 1,0;

Y_N – коэффициент долговечности:

,

где N_F0 – базовое число циклов напряжений. Для сталей N_F0 = 4*10⁶ .

Так как расчетное число циклов напряжений для шестерни N_K1 = 234*10⁷ и для колеса N_K2 = 117*10⁷ больше базового числа циклов N_F0 = 4*10⁶, то принимаем Y_N=1,0.

Допускаемые напряжения изгиба:

– для шестерни – МПа;

– для колеса – МПа.

Определение межосевого расстояния: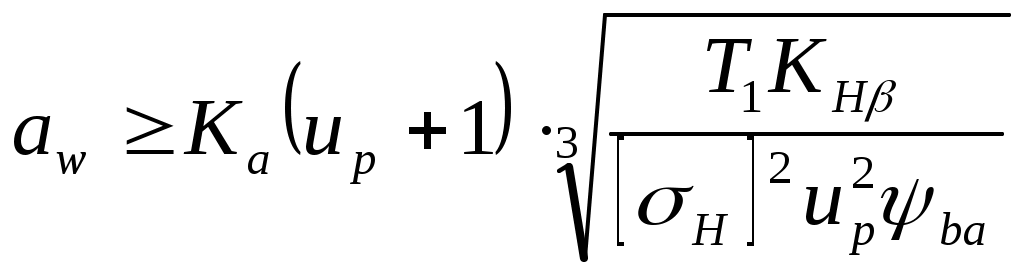

, мм,

где K_a= 450 МПа^1/3 – вспомогательный коэффициент;

u – передаточное число, u = 2,0

T₁ – вращающий момент на шестерне, Т₁ = 67,034 Н*м;

K_H – коэффициент нагрузки, для прямозубой передачи предварительно принимаем К_н = 1,3;

_ψbа– коэффициент ширины венца колеса. При симметричном расположении прямозубых колес относительно опор выбираем _ψbа= 0,315.



Принимаем из ряда стандартных чисел (с.5) а_w = 112 мм.

4) Определение модуля передачи

Минимальное значение модуля из условия прочности на изгиб

, мм,

где K_m = 6,8·10³ – для прямозубой передачи; b₂ – ширина венца колеса

0,315*112 = 35,3 мм

Принимаем b₂ = 36 мм.



Максимально допустимый модуль передачи:

2*112 / [17*(2 + 1)] = 4,39 мм

Принимаем по ГОСТ 9563-80 стандартное значение окружного модуля: m=2,5мм.

5) Определение суммарного числа зубьев шестерни и колеса

.

Принимаем z_Σ = 90

6) Определение числа зубьев шестерни и колеса



Принимаем z₁ = 30.

Так как z₁ = 30> z_min = 17, то зубчатые колеса изготовляются без смещения исходного контура ( .

Число зубьев колеса: z₂ = z- z₁ =90-30=60

7) Уточнение передаточного числа

=60/30=2,00

Отклонение от заданного передаточного числа:



8) Уточнение межосевого расстояния

=2,5*90/2=112,000 мм

9) Определение размеров зубчатых колес

диаметры делительные:

=2,5*30= 75,00 мм

=2,5*60= 150,00 мм

диаметры вершин зубьев:

d_a1 =d₁+ 2m_n =75,00 + 2 * 2,5 = 80,00 мм;

d_a2 = d₂ + 2 m_n = 150,00+ 2 *2,5 = 155,00 мм;

ширина колеса b₂ = _ba*a_w = 0,315 * 112 =35,3 мм, примем 36мм;

ширина шестерни b₁ = b₂ + 5 мм = 41,0 мм.

10) Размеры заготовок

Диаметр заготовки шестерни

80,00+6=86,00 мм

Для колеса с выточками:

– толщина диска 0,5*36 = 18,00 мм

– толщина обода заготовки колеса = 8*2,5 = 20 мм

Предельные размеры заготовок для стали 45:

D_пр = 80 мм; S_пр = 80 мм.

Условия пригодности заготовок выполняются, так как D_заг = D_пр, ^C_заг ^{< S}_пр ^{и S}_заг^{< S}_пр.

11) Определение усилий в зацеплении

Окружная сила:

=(2000*67,034) / 75,00 = 1788 Н

Радиальная сила:

= 1788 * tg20= 650 Н

12) Проверочный расчет передачи на контактную прочность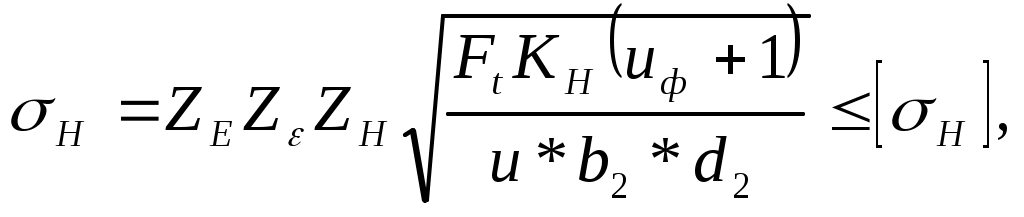



где Z_Е = 190 МПа^1/2 -коэффициент, учитывающий механические свойства материалов сопряженных колес;

Z_ε – коэффициент, учитывающий суммарную длину контактных линий. Для прямозубых колес



ε_а – коэффициент торцевого перекрытия;

=[1,88-3,2*(1/30+1/60)]= 1,72

Z_H – коэффициент, учитывающий форму сопряженных поверхностей зубьев. Для прямозубых передач Z_H ≈ 2,49 ;

u = 2,0 – фактическое передаточное число;

K_H – коэффициент нагрузки K_H = K_Hβ K_Hν ,

где K_Hβ – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий.

При = 36 / 75,00 = 0,48, твердости зубьев колес ≤ 350 НВ и симметричном расположении колес относительно опор K_Hβ = 1,025

K_Hν – коэффициент, учитывающий динамическую нагрузку.

Окружная скорость колес:



Для прямозубой передачи назначаем 8-ю степень точности изготовления.

При ν = 4,12 м/с и 8-й степени точности изготовления передачи K_Hν = 1,200

K_H = 1,025*1,200 = 1,230

Расчетное контактное напряжение:



13) Проверочный расчет передачи на выносливость при изгибе

МПа,

где K_F – коэффициент нагрузки;

Y_FS – коэффициент, учитывающий форму зуба:



z_ν – эквивалентное число зубьев колес;

х – коэффициент смещения;

Y_β – коэффициент, учитывающий наклон зуба, Y_β = 1;

Y_ε – коэффициент, учитывающий перекрытие зубьев, Y_ε = 1.

Для прямозубых передач без смещения исходного контура

х₁ = х₂ = 0 и z_ν = z .

Для шестерни 3,47+13,2/30 = 3,91

для колеса 3,47+ 27,9/60 = 3,94

Коэффициент нагрузки: ,

где K_Fν – коэффициент, учитывающий динамическую нагрузку. При ν = 4,12 м/с и 8-й степени точности K_Fν = 1,400

K_Fβ – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий:

K_Fβ =1+1,5*( K_Hβ -1)=1+1,5*(1,025-1)=1,038

Тогда K_F =1,400*1,038= 1,454

Расчетное напряжение изгиба в зубьях колеса:



Расчетное напряжение изгиба в зубьях шестерни: