синтез устройства летательного аппарата. Техническое задание на курсовое проектирование Вариант 1, легкий самолет 1
 Скачать 481.84 Kb. Скачать 481.84 Kb.
|
|
Техническое задание на курсовое проектирование Вариант 1.1, легкий самолет 1. Спроектировать и проанализировать работу в замкнутой системе статического автопилота угла тангажа со жесткой обратной связью. Исходные данные: Объект управления – легкий самолет при условиях полета: H=11км; М=0,9; τа =3,8с. Коэффициенты уравнений:
Требования статичности и динамической точности САУ угловым движением самолета по каналу тангажа: При расчете параметров канала тангажа автопилота в качестве заданных значений переходного процесса принимают следующие значения [1]:  Содержание
Введение Системы автоматического управления (САУ) летательными аппаратами (ЛА) и их силовыми установками (СУ) можно отнести к числу важнейших направлений авиационной науки и техники. В настоящее время бортовая САУ полетом превратилась из средства, только облегчающего пилоту процесс пилотирования самолетом, в средство эффективной эксплуатации современного летательного аппарата. Движение ЛА можно рассматривать состоящим из движения центра масс и движения вокруг центра масс. Необходимость управления угловым движением вызывается тем, что ЛА должен заниматься вполне определенное положение по отношению к вектору скорости центра масс. Для управления угловым движением применяются в автопилотах соответствующие контуры управления (контуры тангажа, крена, рыскания). Управление движением центра масс необходимо для того, чтобы ЛА совершал полет по заданной траектории, которая в определенном смысле должна быть оптимальной. Автоматическое удержание центра масс ЛА на заданной траектории осуществляется специальными контурами управления, замыкаемыми через автопилот (контуры управления высотой, пройденным расстоянием, боковым отклонением и т.д.) Углом тангажа называется угол, образуемый продольной осью ЛА с горизонтальной плоскостью. Изменение угла тангажа определяет продольное движение самолета. Система управления углом тангажа самолета служит для выдерживания нужной траектории движения в вертикальной плоскости. При этом предусматривается возможность изменения заданного угла тангажа вручную с места пилота или автоматически по сигналам, вырабатываемым системой траекторного управления. Процесс управления углом крена сводится к следующему. При появлении рассогласования 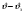 происходит отклонение руля на величину происходит отклонение руля на величину 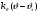 и создается поперечный момент Mz, пропорциональный рассогласованию и создается поперечный момент Mz, пропорциональный рассогласованию 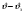 , под действием которого поперечная ось самолета будет поворачиваться в сторону уменьшения величины , под действием которого поперечная ось самолета будет поворачиваться в сторону уменьшения величины 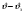 . . 1. Структурная схема САУ 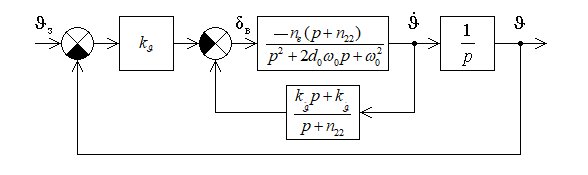 Рис. 1. Структурная схема статической системы управления углом тангажа с ЖОС Рассмотрим статическую систему автоматического управления углом крена (рис. 1). Закон управления системы берем 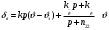 (1) (1)где 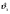 – заданное значение угла крена; – заданное значение угла крена; 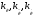 – передаточные числа. – передаточные числа.2. Дифференциальное уравнение САУ Линейная математическая модель бокового движения самолета описывается следующими дифференциальными уравнениями [3]:  где 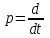 , , 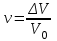 , , 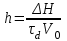 , , 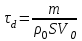 – аэродинамическая постоянная ЛА, – аэродинамическая постоянная ЛА, 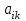 – коэффициенты, – коэффициенты, 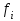 –возмущения, –возмущения, 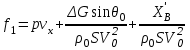 , , 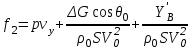 , , 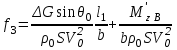 , , 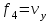 , , 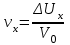 , , 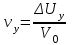 , , 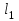 – расстояние центра масс сбрасываемого груза до центра масс ЛА. – расстояние центра масс сбрасываемого груза до центра масс ЛА.Входящие в уравнение (2) коэффициенты nik являются известными функциями времени. В короткие промежутки, не превосходящие постоянную времени τа более чем на один порядок, их можно считать постоянными. При полете с незначительным изменением высоты членами n14h, n24h , n34h в уравнениях (2) можно пренебречь. Тогда в случае горизонтального полета из системы (2) получим 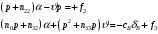 (3) (3)Отсюда находим выражения для передаточных функций, полагая 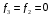 : :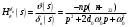 (4) (4)где 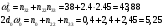 Решая уравнение (1) совместно с уравнениями (3) получим дифференциальное уравнение СА: 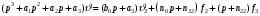 (5) (5)где 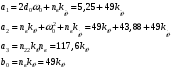 3. Передаточные функции САУ Передаточная функция замкнутой системы по задающему воздействию 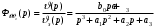 (6) (6) Передаточные функции замкнутой системы по возмущающим воздействиям 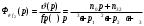 (7) (7)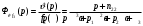 (8) (8) 4. Расчет передаточных чисел автопилота Выбор параметров системы управления следует производить из условий неискаженного воспроизведения заданного угла тангажа 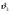 при слабом реагировании на возмущения f3 и f2 . Для внешнего замкнутого контура (см. рис. 1) можно написать: при слабом реагировании на возмущения f3 и f2 . Для внешнего замкнутого контура (см. рис. 1) можно написать: 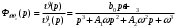 (9) (9) где: 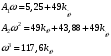 (9.1) (9.1)Известно, что параметры Вышнеградского A1 и A2 соответствуют оптимальному переходному процессу, если они меняются от двух до трех. Однако, анализ уравнений показывает, что эти соотношения не могут быть удовлетворены при принятом законе управления автопилота [3], т.е. невозможно осуществить движение, соответствующее наилучшему переходному процессу. Для выбора параметров системы поступим следующим образом. Потребуем, чтобы частота системы ω, косвенно связанная с временем регулирования, имела определенное значение. Если задать ω, то из третьего соотношения получим 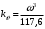 (10) (10)При ω=5, получим 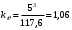 Задавая A1=3, из первого соотношения (9.1) получим: 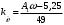 (11) (11) или 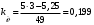 Тогда получим из второго соотношения получим: 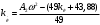 (12) (12) или 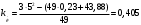 Полученные передаточные числа безразмерные величины. Для получения размерных величин необходимо воспользоваться зависимостями: 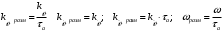 (13) (13)где τа – аэродинамическая постоянная времени. Размерные передаточные числа показывают, на какой угол в градусах необходимо отклонить руль горизонтали при отклонении самолета по углу крена на 1 град, или по угловой скорости крена на 1 град/с. При τа=3,8с получаем следующие значения размерных коэффициентов 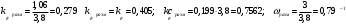 Далее при анализе и моделировании используются безразмерные величины. 5. Анализ устойчивости САУ Характеристическое уравнение замкнутой системы имеет вид: 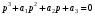 где 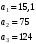 Тогда определитель Гурвица может быть представлен в виде 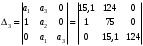 Условие устойчивости САУ: 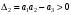 (14) (14)или для данного случая 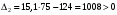 Это условие выполняется, следовательно, полученная система является устойчивой. Запас устойчивости САУ можно определить с помощью расчета частотных характеристик в пакете Control системы Matlab. Программа анализа САУ в пакете Control представлена в приложении 1. Амплитудная и фазовая частотные характеристики разомкнутой САУ, полученные в результате расчета, приведены в приложении 2. Запас устойчивости САУ по фазе составляет 126 градусов. 6. Анализ статической точности САУ Рассматриваемая система обладает статической ошибкой при действии возмущений. Чтобы определить эту ошибку в уравнении (5), примем 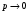 . . Тогда при условии 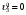 найдем найдем 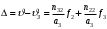 (15) (15)или 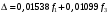 . . 7. Моделирование САУ Цифровое моделирование переходных процессов, происходящих в САУ при подаче на вход единичного задающего воздействия 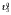 и единичного возмущения f2 , производилось с использованием пакета SimuLink системы Matlab. Схема моделирования приведена в приложении 3. и единичного возмущения f2 , производилось с использованием пакета SimuLink системы Matlab. Схема моделирования приведена в приложении 3. График переходного процесса по задающему воздействию приведен в приложении 4, по возмущению – в приложении 5. По оси абсцисс отложены значения безразмерного времени. Для получения размерного (действительного) времени значения абсцисс необходимо умножить на аэродинамическую постоянную времени самолета τа=3.8. Следовательно, переходные процессы в САУ являются монотонными, время регулирования равно: tрег=1,275⸱3,8=4,845с, что соответствует заданию; величина статической ошибки по возмущению f2 равна нулю. Заключение В ходе курсового проектирования был разработан и проанализирован статический автопилот угла тангажа с жесткой обратной связью. Анализ устойчивости данной САУ показал, что исследуемая система является устойчивой по алгебраическому критерию Гурвица. Анализ статической точности САУ показал статическую ошибку 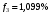 . .Было произведено цифровое моделирование переходных процессов, происходящих в САУ при подаче единичного задающего воздействия и единичного возмущения, с использованием пакета Simulink системы Matlab. После цифрового моделирования переходных процессов, происходящих в САУ было определено время регулирования tрег=4,845, перерегулирование системы 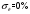 . Характер переходного процесса монотонный. . Характер переходного процесса монотонный. По графику ЛФЧХ определен запас устойчивости САУ по фазе, который составляет 126 градуса. Исходя из требований статической и динамической точности САУ угловым движением самолета по каналу тангажа: 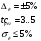 и с учетом полученных значений, видно, что спроектированная САУ, удовлетворяет требованиям статической и динамической точности и обладает запасами устойчивости. Переходной процесс оптимальный т.е монотонный.  |
