Математические основы цифровой обработки сигналов. Вариант 16. Техническое задание
 Скачать 381.94 Kb. Скачать 381.94 Kb.
|
|
Техническое задание Задание на курсовую работу содержит схему анализируемой цепи и входной сигнал в виде ограниченного импульса, параметры которого указаны на рисунке. Исходные данные:
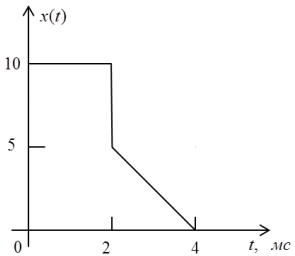 Рисунок 1 – Входной сигнал 1. Исследование входного сигнала x(t). 1.1 Определить спектр входного аналогового сигнала x(t). Построить амплитудный и фазовый спектр входного сигнала в диапазоне 0 – 3 кГц с шагом 0,1 кГц. Определить верхнюю частоту спектра fв. Спектральная плотность входного и выходного сигналов, передаточная функция и их графики Для нахождения спектральной плотности входного сигнала функция U1(t) представляется в виде суммы «четырех» простейших функций:  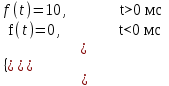 , изображение , изображение 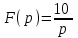 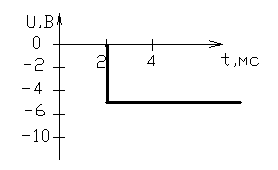 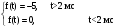 , изображение , изображение 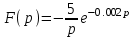 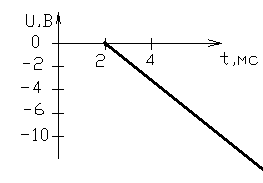 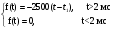 , изображение , изображение 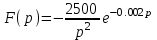 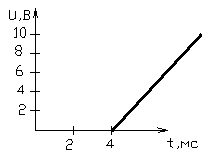 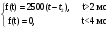 , изображение , изображение 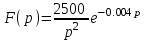 Изображение входного сигнала записывается как сумма изображений «простейших» функции. 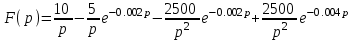 Заменяя в последнем выражении p на jω, получаем спектральную плотность входного сигнала 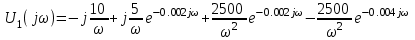 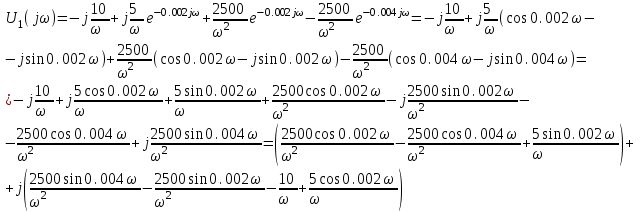 Амплитудная характеристика спектральной плотности входного сигнала 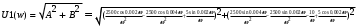 Фазовая характеристика спектра входного сигнала Фазовая характеристика спектра входного сигнала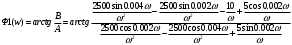
АЧХ спектральной плотности входного сигнала 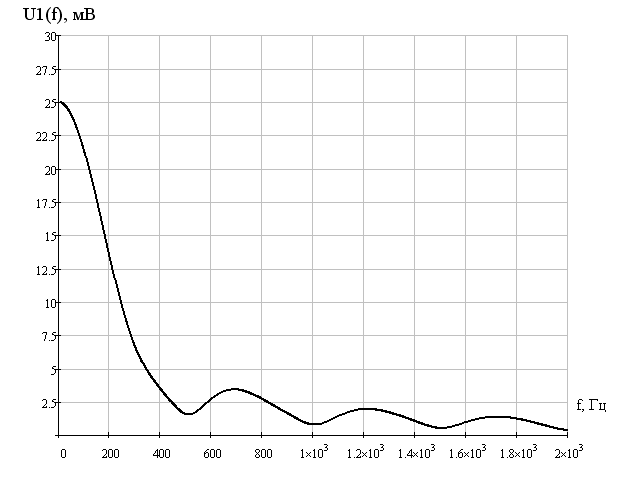 ФЧХ спектральной плотности входного сигнала 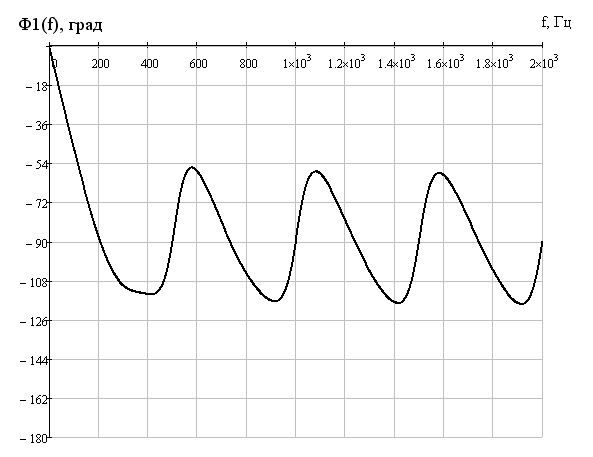 1.2 Определить частоту дискретизации fд. Среди значений 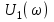 , приведенных в таблице, определяем максимум модуля спектральной плотности: , приведенных в таблице, определяем максимум модуля спектральной плотности: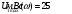 Находим частоту, после которой значение U1(w) не превышает уровень 0,1U1max=2,5 мВс. Я выбрал f=1,25 кГц. Эта частота принимается за верхнюю границу спектра входного сигнала, и частота дискретизации берется равной fд=2,5 кГц. 1.3 Определить период дискретизации Тд и записать отчеты входного дискретного сигнала x(n). Период дискретизации при fд=2.5кГц равен Т=0,4мс.
Функция U1(t) при t=2 мс изменяется скачком от значения 0 до 10 В. При записи массива U1(n) для t=2мс берется среднее арифметическое этих значенийU1(0)=5В. Функция U1(t) при t=4 мс изменяется скачком от значения 10 до 5 В. При записи массива U1(n) для t=4мс берется среднее арифметическое этих значенийU1(0)=7,5В. 1.4 Построить график входного дискретного сигнала x(n). 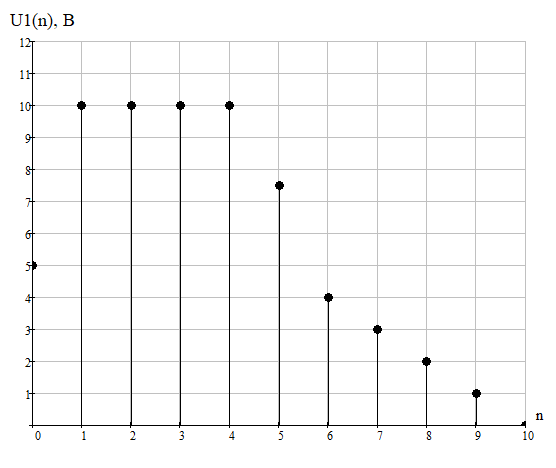 График импульсной характеристики входного сигнала. 1.5 Определить спектр входного сигнала x(n) с шагом ωд/10. Построить амплитудный и фазовый спектр. Спектральные характеристики дискретизированного сигнала U1(n) могут быть вычислены на любой частоте, однако для сокращения объема расчетов целесообразно ограничиться 4 значениями частоты. Спектральная плотность дискретизированного сигнала U1(n) на любой частоте может быть вычислена по формуле: 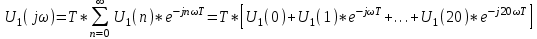 Значения спектра входного сигнала:
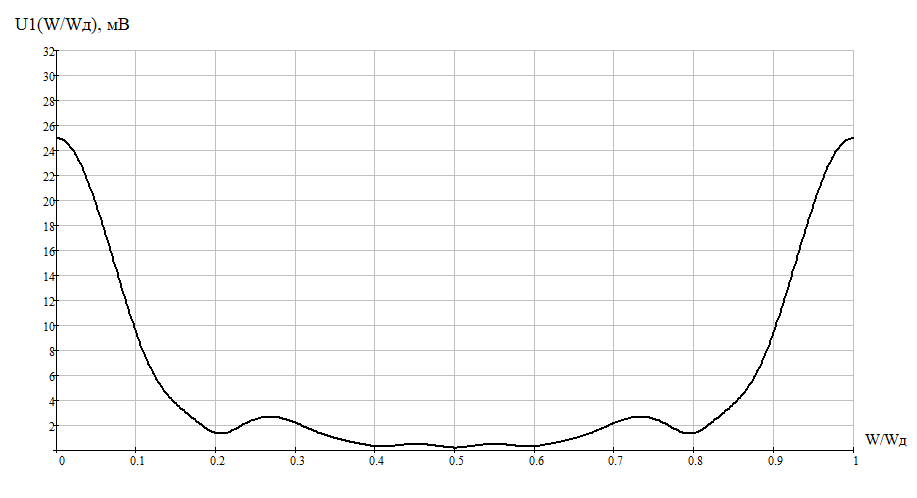 График АЧХ дискретизированного сигнала 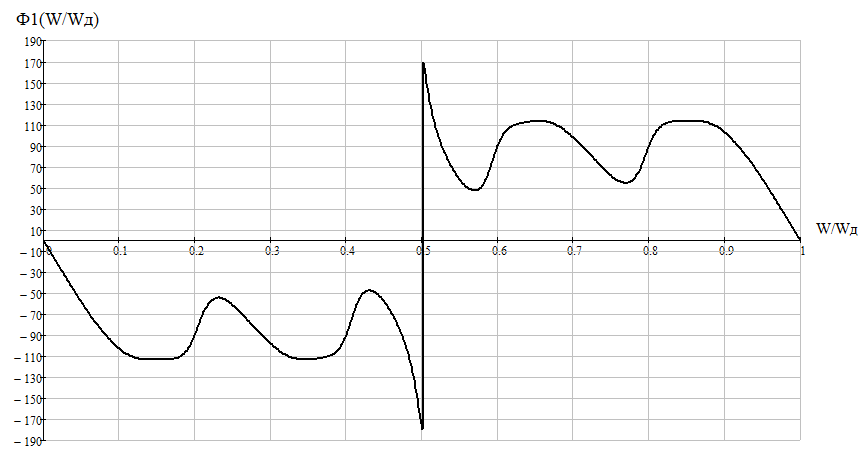 График ФЧХ дискретизированного сигнала 2. Исследование характеристик дискретной цепи (ДЦ). 2.1 Определить разностное уравнение ДЦ. Если известны параметры линейной дискретной системы, то взаимосвязь между входным воздействием x(n) и реакцией y(n) описывается разностным уравнением вида: 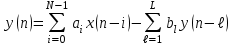 , (1.1) , (1.1)где 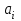 , , 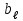 - коэффициенты уравнения (вещественные константы); - коэффициенты уравнения (вещественные константы);x(n), y(n) - воздействие и реакция (вещественные или комплексные сигналы); N - число прямых связей; L - число обратных связей; 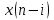 , , 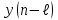 - воздействие и реакция, задержанные на i и - воздействие и реакция, задержанные на i и 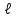 периодов дискретизации соответственно. периодов дискретизации соответственно.Важно помнить, что: - разностное уравнение должно отображать все пути прохождения входного сигнала через цепь. Запишем разностное уравнение дискретной цепи, изображенной на рис. 1.1: 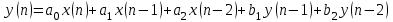 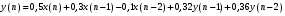 (1.2) (1.2)2.2 Определить с помощью разностного уравнения передаточную функцию H(z) и проверить устойчивость цепи. Известно, что передаточной функцией Н(z) называют отношение z-изображения реакции к z-изображению воздействия при нулевых начальных условиях. Применив z-преобразования к разностному уравнению, получим: 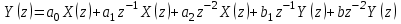 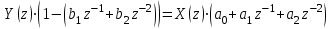 Тогда передаточная характеристика цепи: 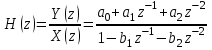 (1.3) (1.3)Запишем передаточную функцию дискретной цепи, изображенной на рис.1.1: 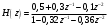 (1.4) (1.4)Дискретная цепь является устойчивой, если полюсы ее передаточной функции лежат внутри единичной окружности z-плоскости, т.е. 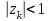 (1.5) (1.5)Чтобы определить, устойчива ли дискретная цепь, показанная на рис.1.1, найдем ее полюсы. Для этого приравняем знаменатель передаточной функции к нулю: 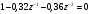 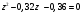 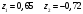 По полученным результатам видно, что условие (1.5) выполняется, т.е. дискретная цепь является устойчивой. Определение импульсной характеристики цепи h(n) 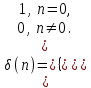 (1.6) (1.6)Признаком нулевых начальных условий является отсутствие реакции при отсутствии воздействия. Важно помнить, что: - как и разностное уравнение, импульсная характеристика описывает дискретную цепь во временной области; - определить импульсную характеристику дискретной системы можно двумя способами: 1. по разностному уравнению, решая его методом прямой подстановки; 2. по передаточной функции 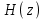 путем деления полинома числителя на знаменатель путем деления полинома числителя на знаменатель- импульсная характеристика нерекурсивной цепи имеет конечную длительность, значения отсчетов равны коэффициентам разностного уравнения; - импульсная характеристика рекурсивной цепи имеет бесконечную длительность; - для достижения необходимой точности при вычислении импульсной характеристики надо учесть все отсчеты, значения которых превышают 10% от максимального значения 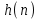 . .1 способ: Допустим, что на вход дискретной цепи действует дельта-функция вида 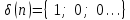 . Тогда, согласно разностному уравнению цепи: . Тогда, согласно разностному уравнению цепи: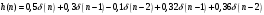 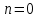 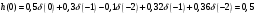 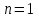 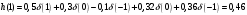 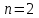 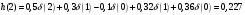 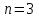 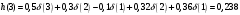 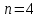 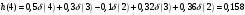 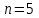 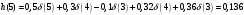 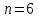 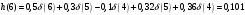 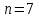 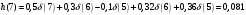 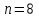 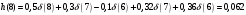 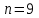 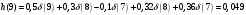 Так как 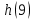 составляет ≈ 8,5 % от составляет ≈ 8,5 % от 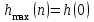 , т.е. не превышает 10%, дальнейшие отчеты импульсной характеристики цепи считать не имеет смысла. , т.е. не превышает 10%, дальнейшие отчеты импульсной характеристики цепи считать не имеет смысла.2 способ: Импульсную характеристику дискретной цепи можно найти по передаточной функции, выполнив ее обратное z-преобразование. Обратное z-преобразование передаточной функции можно осуществить путем последовательного деления полинома числителя Н(z) на знаменатель с поочередным выделением слагаемых вида 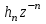 . .Выполним деление передаточной функции Н(z): 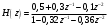 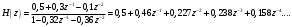 Деление осуществляем до тех пор, пока не достигнем 10% от hmax(n). Таблица 1.1 Импульсная характеристика дискретной цепи
Построим график импульсной характеристики цепи: 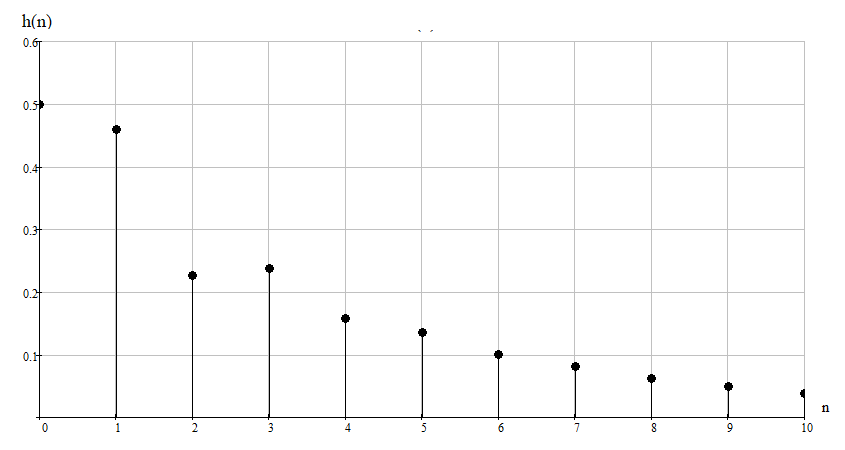 Рисунок 1.2 - Импульсная характеристика цепи Определение АЧХ и ФЧХ цепи Частотная характеристика линейной дискретной цепи 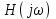 - фурье-изображение импульсной характеристики - фурье-изображение импульсной характеристики 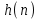 . Также выражение . Также выражение 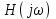 можно получить из передаточной функции цепи можно получить из передаточной функции цепи 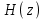 , выполнив замену , выполнив замену 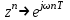 . . 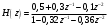 (1.8) (1.8)Как и всякую комплексную функцию, 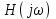 можно представить через модуль и аргумент можно представить через модуль и аргумент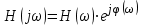 , (1.9) , (1.9)где 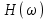 - амплитудно-частотная характеристика (АЧХ) цепи, - амплитудно-частотная характеристика (АЧХ) цепи,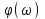 - фазо-частотная характеристика (ФЧХ) цепи. - фазо-частотная характеристика (ФЧХ) цепи.Для определения частотных характеристик цепи и сигнала часто применяют нормирование по частоте:  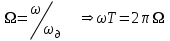 (1.10) (1.10)Запишем передаточную функцию исходной цепи 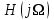 . Согласно выражению (1.8), получим: . Согласно выражению (1.8), получим: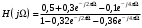 (1.11) (1.11)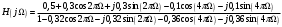 (1.12) (1.12)Амплитудно-частотная характеристика дискретной цепи: 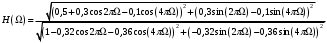 (1.13) (1.13)Фазо-частотная характеристика дискретной цепи: 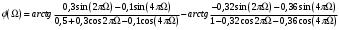 (1.14) При расчетах важно помнить, что: 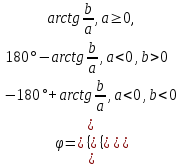 Расчеты удобно свести в таблицу: Таблица 1.2 – Частотные характеристики цепи
Так как частотные характеристики дискретных цепей (сигналов) являются непрерывными периодически повторяющимися функциями, достаточно построить частотные характеристики только для одного периода, соответствующего 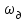 . .тогда 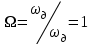 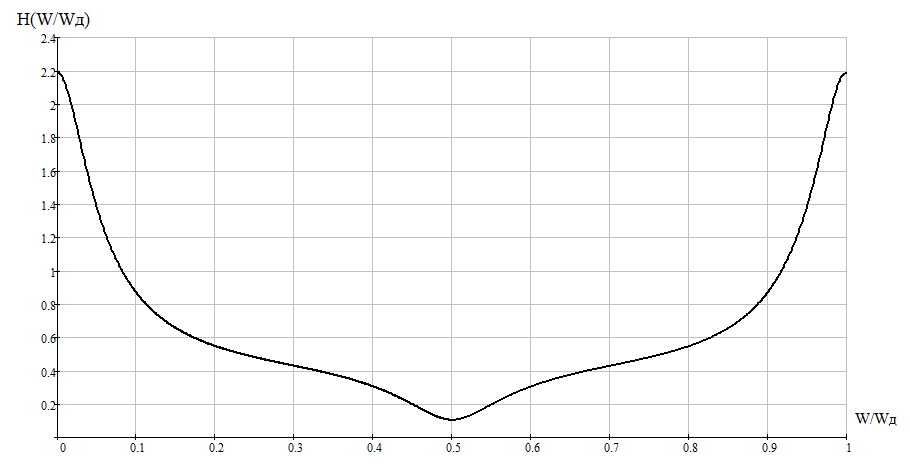 Рисунок 1.3 - АЧХ дискретной цепи 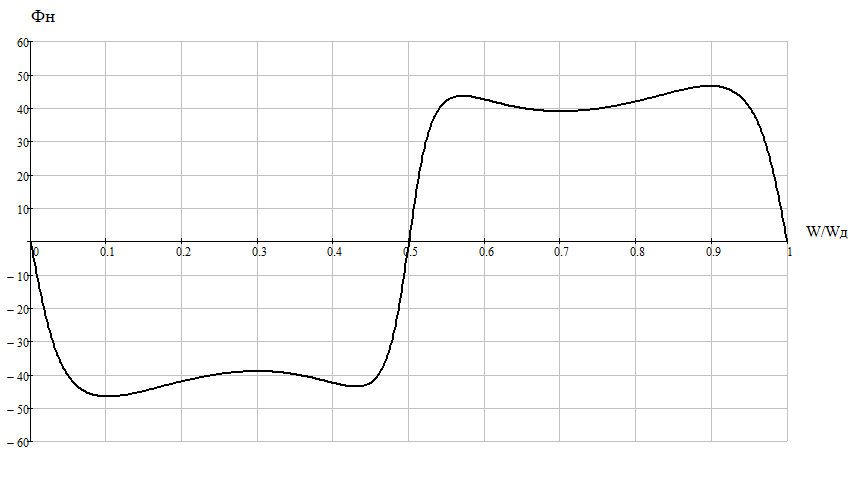 Рисунок 1.4 – ФЧХ дискретной цепи Как видно из рисунков 1.3 и 1.4 АЧХ является непрерывной периодически повторяющейся четной функцией, а ФЧХ – непрерывной периодически повторяющейся нечетной функцией. 2. Прохождение дискретного непериодического сигнала через ДЦ 2.3 Определение сигнала на выходе дискретной цепи На вход дискретной цепи, изображенной на рис.1.1, действует дискретный непериодический сигнал x(n). Для определения сигнала на выходе дискретной цепи y(n) можно воспользоваться несколькими способами: - по разностному уравнению ДЦ; - по формуле линейной свертки. Важно помнить, что число отчетов дискретного сигнала на выходе ДЦ определяется, как: 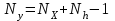 (2.5) (2.5)где 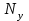 - число отчетов выходного сигнала y(n); - число отчетов выходного сигнала y(n);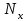 - число отчетов входного сигнала x(n); - число отчетов входного сигнала x(n);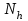 - число отчетов импульсной характеристики. - число отчетов импульсной характеристики.В нашем случае 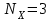 , , 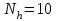 поэтому поэтому 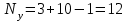 отчетов. отчетов.Найдем сигнал на выходе дискретной цепи, воспользовавшись формулой линейной свертки: 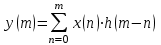 , , 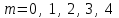 (2.6) (2.6)где 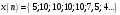 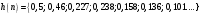 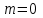 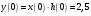 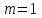 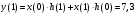 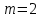 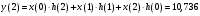 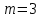 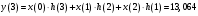 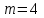 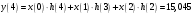 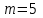 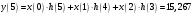 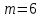 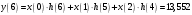 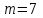 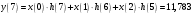 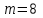 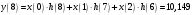 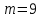 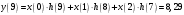 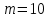 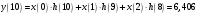 Нетрудно заметить, что последние два отчета выходного сигнала, рассчитанные разными способами, незначительно отличаются по величине. Это различие обусловлено ограничением импульсной характеристики ДЦ, которая используется для расчета выходного сигнала с помощью линейной свертки. Построим график выходного сигнала y(n). 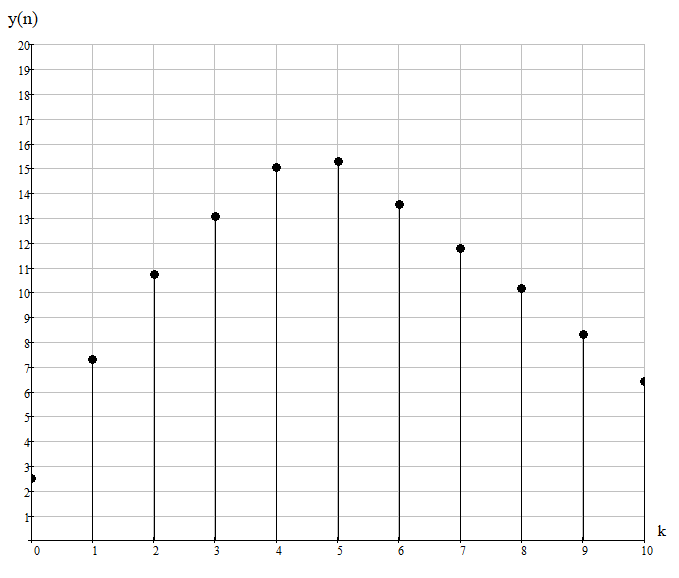 Рисунок 2.4 – График выходного сигнала y(n) 2.4 Определение спектра сигнала на выходе дискретной цепи Для нахождения спектра выходного сигнала можно было бы воспользоваться прямым преобразованием Фурье для дискретных сигналов. В случае, когда уже известны спектр входного сигнала и частотные характеристики ДЦ, рациональнее использовать теорему наложения (свертки). 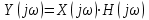 (2.7) (2.7)В частности, амплитудный спектр выходного сигнала: 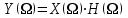 ; ;фазовый спектр выходного сигнала: 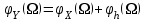 . .Сведем все расчеты в таблицу: Таблица 2.2 - Частотные характеристики выходного сигнала
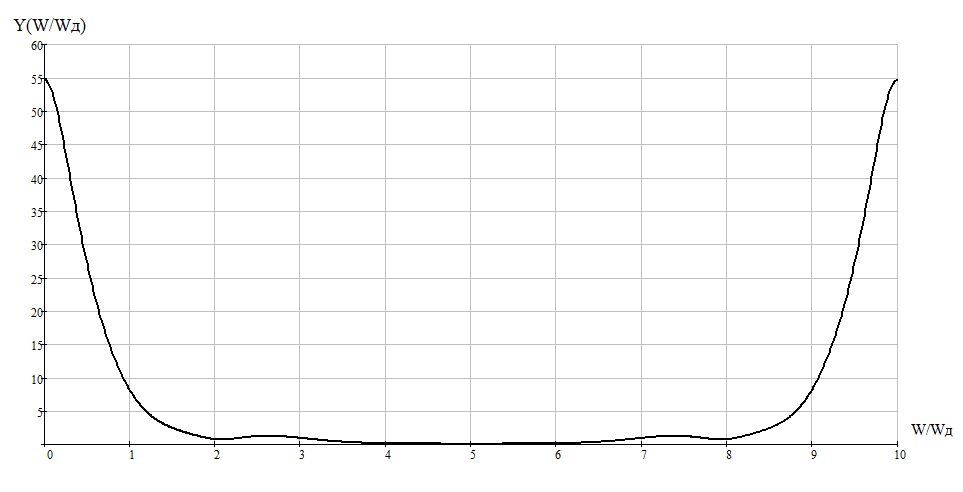 Рисунок 2.5 - Амплитудный спектр выходного сигнала 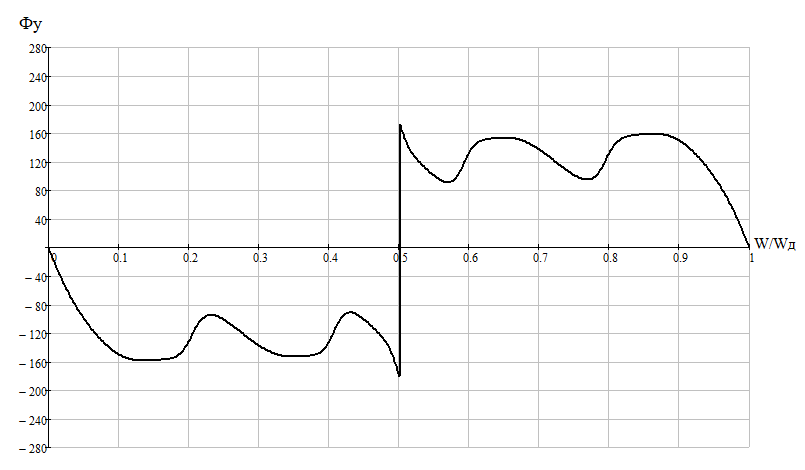 Рисунок 2.6 – Фазовый спектр выходного сигнала |
