фывфыв. Техническое задание вариант 4 4 1 Структурный анализ механизма 6 2 Кинематический синтез механизма 11
 Скачать 0.63 Mb. Скачать 0.63 Mb.
|
3. Синтез зубчатых механизмов3.1 Расчет приводаПередаточное отношение привода 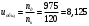 Передаточное отношение простой ступени 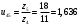 Передаточное отношение планетарной ступени 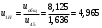 Передаточное отношение планетарной ступени 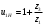 (3.1) (3.1)При заданном передаточном отношении u1Н определение чисел зубьев передачи сводится к выполнению следующих операций. 1. Определяем величину 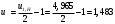 . . 2. Задаём в приемлемой области ряд чисел зубьев z1 =17, 18, 19 и т. д. 3. Вычисляем для каждого значения z1 величину z’2 = u·z1 и округляем полученное число z’2 до ближайшего целого числа z2. 4. Определяем из условия cоосности число зубьев z3 = z1 + 2z2 . 5. Проверяем по таблице 5 отсутствие интерференции между зубчатыми колёсами с числами зубьев z2 и z3 . 6. Определяем величину 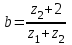 и максимальное число сателлитов из условия соседства Kp = 180 /arcsin b . и максимальное число сателлитов из условия соседства Kp = 180 /arcsin b . 7. Проверяем условие сборки (z1+ z3 )/ K = С, где Кp = 2, 3, 4 - число сателлитов (К < Кp ), С - целое число. 8. Определяем передаточное отношение 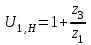 9. Определяем относительную разницу между заданным и полученным передаточными отношениями 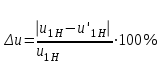 10. Выполняем анализ полученных результатов и выбор оптимального варианта чисел зубьев колёс передачи по наименьшим габаритам и наименьшей разнице Δu. Выполняя последовательно перечисленные операции синтеза планетарной передачи, получим ряд результатов, которые помещены в таблице 1.2. Анализируя результаты вычислений, содержащиеся в таблице 5, принимаем вариант № 5, как имеющий наименьшую разницу 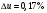 и z3>85 т. е. z1 = 23, z2 = 34, z3 = 91, k=3 u’1H =4,957. и z3>85 т. е. z1 = 23, z2 = 34, z3 = 91, k=3 u’1H =4,957. Число сателлитов К принимаем равным 4. 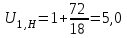 Таблица 3.1 - Результаты расчёта
Проверяем в планетарном редукторе выполнение условий: исключения заклинивания зацеплений: а) колес 1, 2: 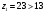 , , 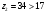 – условие выполняется; – условие выполняется;б) колес 2, 3: 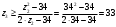 , 91>33 – условие выполняется; , 91>33 – условие выполняется; исключения интерференции зубьев колес 2, 3: 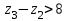 ; ; 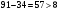 - условие выполняется; - условие выполняется;соосности колес 1, 3: 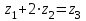 , , 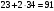 , , 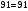 - условие выполняется; - условие выполняется;соседства 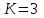 сателлитов 2: сателлитов 2: 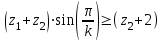 , , 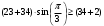 , , 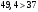 - условие выполняется; - условие выполняется;сборки (установки) сателлитов 2: 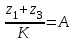 , , 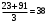 , , 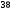 –целое число - условие выполняется. –целое число - условие выполняется.Частоты вращения зубчатых колес и валов: вала I и колеса 1: 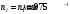 ; ;водила H, вала III и колеса 4: 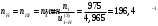 ; ;колеса 5 и вала IV: 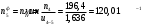 , отклоняется от требуемого по заданию , отклоняется от требуемого по заданию 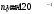 на на 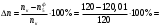 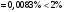 , что приемлемо. , что приемлемо.Делительные диаметры зубчатых колес:  , ,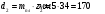 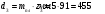 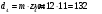 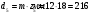 Вычерчиваем схему редуктора на основании геометрического расчёта. Масштабом построения зададимся из условия размещения схемы на листе  . . | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||