фывфыв. Техническое задание вариант 4 4 1 Структурный анализ механизма 6 2 Кинематический синтез механизма 11
 Скачать 0.63 Mb. Скачать 0.63 Mb.
|
 СОДЕРЖАНИЕВведение 3 Техническое задание – вариант 4 4 1 Структурный анализ механизма 6 2 Кинематический синтез механизма 11 2.1 Построение планов положений механизма 11 2.2 Построение плана скоростей механизма 13 3. Синтез зубчатых механизмов 17 3.1 Расчет привода 17 3.2 Синтез эвольвентного зубчатого зацепления 20 2Обозначение, формула 20 4 Синтез кулачкового механизма 23 4.1 Синтез структурной схемы механизма 23 4.2 Определение основных размеров механизма 23 4.3 Расчет масштабных коэффициентов 24 4.2. Построение диаграммы . 25 4.3. Построение диаграммы . 25 4.4 Построение кулачкового механизма 26 Список использованных истчоников 28 ВведениеРазвитие современной науки и техники неразрывно связано с созданием новых машин, повышающих производительность и облегчающих труд людей, а так же обеспечивающих средства исследования законов природы и жизни человека. Понятием машины охватывается большое число самых различных объектов, применяемых человеком для своих трудовых и физиологических функций. Машина есть устройство, создаваемое человеком для изучения и использования законов природы с целью облегчения физического и умственного труда, увеличение его производительности и облегчения путем частичной или полной замены человека в его трудовых и физиологических функциях. Объектом исследования данного курсового проекта механизма пресс-автомата для холодного выдавливания. Основной механизм (рис.1) состоит из кривошипа 1, шатунов 2 и 4, коромысла 3 и рабочего ползуна 5. Ведущее звено 1 приводится в движение от электродвигателя при помощи планетарного редуктора и цилиндрической зубчатой передачи z4-z5. Высадочный ползун 5 с закрепленным в нем пуансоном при движении влево (рабочий ход) деформирует заготовку. Диаграмма усилий высадки представлена на рис. 1. Подача заготовки производится при холостом ходе (вправо) ползуна 5 посредством кулачкового механизма. Механизм подачи состоит из кулачка, закрепленного на одном валу с кривошипом, и толкателя, снабженного приспособлением для подачи заготовки. Для реализации целей курсового проекта были решены следующие задачи: - изучение и систематизация литературы по дисциплине «Теория механизмов и машин»; - проведен разносторонний анализ рычажного механизма; - выполнено проектирование зубчатой передачи; - проведен синтез кулачкового механизма. Работа состоит из введения, трех глав, трех чертежей, списка литературы и нормативных ссылок. Техническое задание – вариант 4Тема 5. Проектирование механизмов пресс-автомата для холодного выдавливания 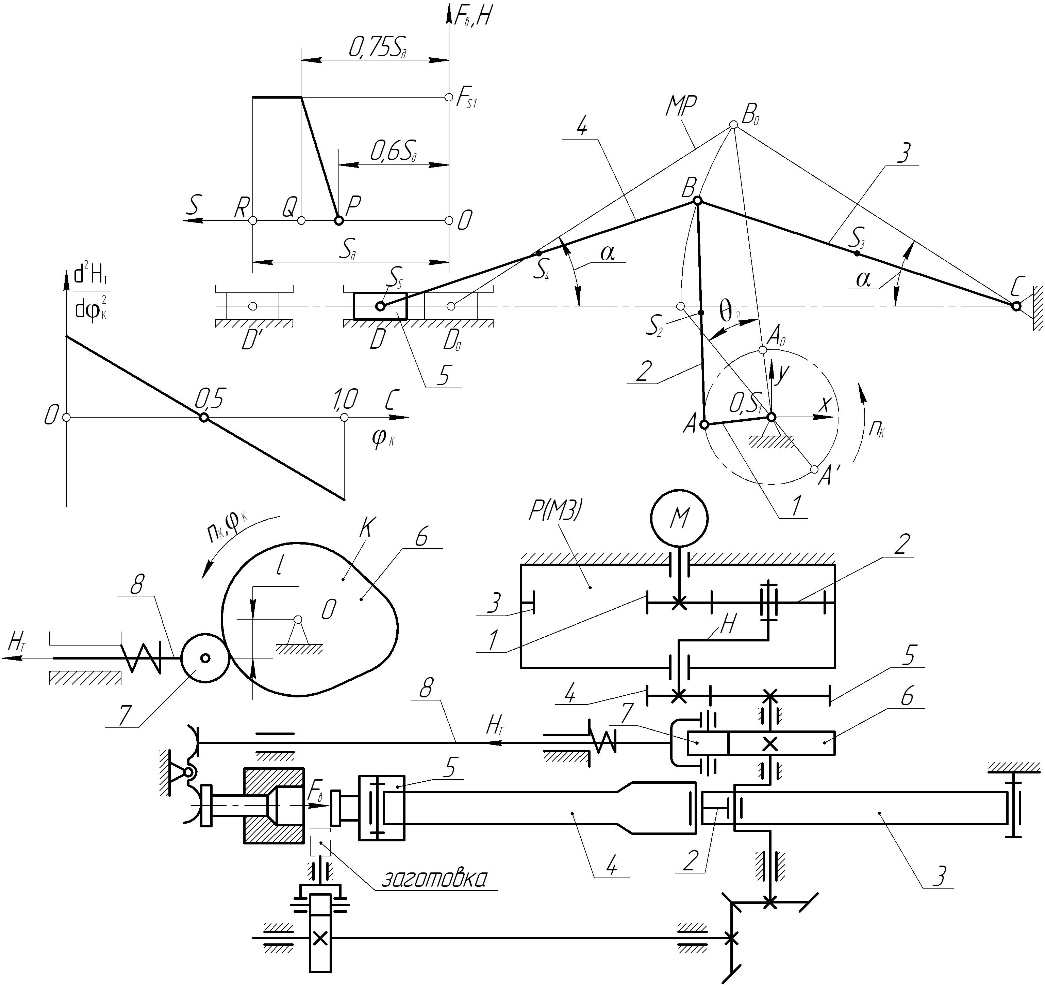
1 Структурный анализ механизмаИсследуемый механизм, кинематическая схема, которого приведена на рис. 1.1 служит для преобразования вращательного движения кривошипа 1 (входное звено) в поступательное движение звена 5. 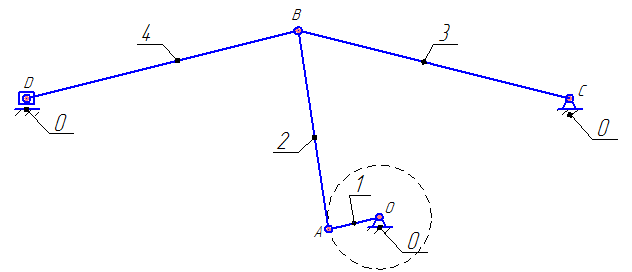 Рисунок 1.1 –Кинематическая схема механизма Определяем степень подвижности механизма по формуле: W=3×n ‑ 2×p5 ‑ p4, где n - число подвижных звеньев; P5 - число кинематических пар первого класса; p4 – число кинематических пар четвертого класса. n=5; p5=7; p4=0. Итак, W=3×5‑2×7‑0=1. Так как W=1 то у механизма одно входное звено. Механизм состоит из 5 звеньев: 0-стойка; 1-кривошип; 2, 4 - шатуны, 3 – коромысло, 5-ползун. Рассмотрим кинематические пары Таблица 1.1 Анализ кинематических пар
Разбиваем рассматриваемую схему на группы звеньев, начиная с выходного звена. Раскладываем механизм на группы Асcура 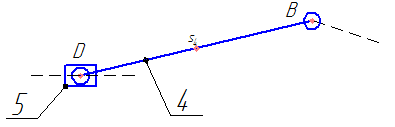 Рисунок 1.2 – Структурная группа 4-5 Данная группа состоит: – из двух подвижных звеньев (шатун 4 и ползун 5), т.е. n =2 ; – двух свободных поводков; – трёх кинематических пар (вращательная 4 – 5, вращательная 3 – 4, поступательная 5 – 0), т.е. p5 =3 . Подставив найденные значения коэффициентов в формулу Чебышева, получаем: W=3n‑2p5‑p4 =3·2‑2·3‑0=0 Равенство нулю подвижности группы доказывает, что рассматриваемая группа звеньев 4 – 5 является структурной группой. Данная группа является: – группой второго класса, так как состоит из двух подвижных звеньев; – группой второго порядка, так как имеется два свободных поводка; – группой второго вида, так как состоит из двух вращательных кинематических пар и одной поступательно(ВВП). Данная группа II класса и 2-го вида 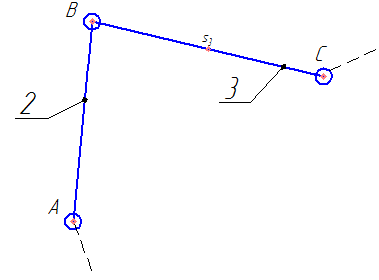 Рисунок 1.3 – Структурная группа 2-3 Данная группа состоит: – из двух подвижных звеньев (шатун 2 и коромысло 3), т.е. n= 2 ; – двух свободных поводков (кривошип 1 и стойка 0); – трёх кинематических пар (вращательная 2 – 3, вращательная 2 – 1, вращательная 3 – 0), т.е. p 5 =3 . Подставив найденные значения коэффициентов в формулу Чебышева, получаем: W=3n‑2p5‑p4 =3·2‑2·3‑0=0 Равенство нулю подвижности группы доказывает, что рассматриваемая группа звеньев 2 – 3 является структурной группой. Данная группа является: – группой второго класса, так как состоит из двух подвижных звеньев; – группой второго порядка, так как имеется два свободных поводка; – группой первого вида, так как состоит из трех вращательных кинематических пар (ВВВ). Данная группа II класса и 1-го вида 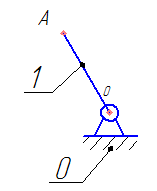 Рисунок 1.4 – Начальный механизм Данная группа состоит: – из одного подвижного звена (кривошип 1) и шарнирно-неподвижной опоры (стойка 0), т.е. n=1; – одной кинематической пары (вращательная 0 – 1), т.е. p 5 = 1. Подставив найденные значения коэффициентов в формулу Чебышева, получаем: W=3n‑2p5‑p4 =3·1‑2·1‑0=1 Подвижность исследуемой группы получилась больше нуля, следовательно она не является структурной группой, а представляет собой первичный (элементарный) механизм, с подвижностью равной единице. Из проведенного анализа следует, что структурная схема механизма состоит из двух структурных групп звеньев и одного первичного механизма. Так как класс механизмов определяется классом наиболее сложной структурной группы, то рассматриваемый рычажный механизм является механизмом 2-го класса, с подвижностью равной единице. 2 Кинематический синтез механизма2.1 Построение планов положений механизмаКинематический синтез выполняют после структурного синтеза, используя составленную структурную схему механизма. Цель синтеза состоит в проектировании оптимальной кинематической схемы механизма на основе выполнения главного условия синтеза – обеспечить заданную кинематическую характеристику движения исполнительного (выходного) звена механизма с требуемой точностью. Кинематическая характеристика может быть задана в виде: – средней скорости и коэффициента KV ,Kωизменения средней скорости выходного звена; – несколькими значениями кинематической функции положения механизма - зависимости координаты выходного звена от обобщенной координаты механизма на входе; – различного вида функции перемещения (траектории движения) выходного звена в определенном диапазоне перемещения входного звена. Кинематический синтез включает в себя: – определение геометрических размеров механизма и его звеньев; – определение параметров работоспособности механизма и их оценку на оптимальность. Геометрические размеры определяют на основе заданной кинематической характеристики движения выходного звена механизма и желательных размеров его отдельных звеньев. Угол перекрытия определяется по формуле 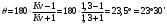 º ºДлина коромысла определяется построением (см. рис. 2.1). Принимаем масштабный коэффициент μl= 0,01 м/мм Тогда на чертеже получим: Н=lН/ μl=0,26/0,01=26 мм 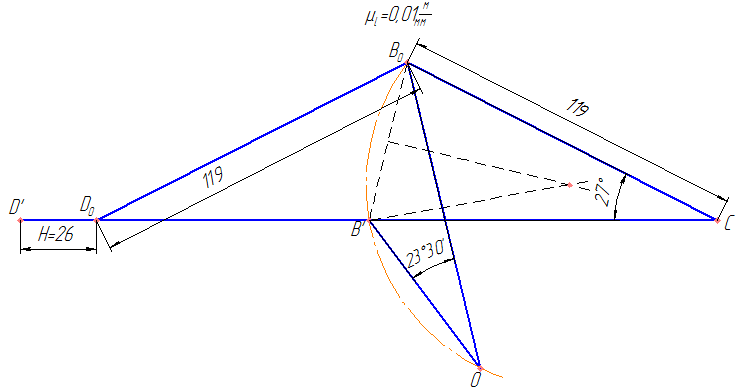 Рисунок 2.1 Из построения получаем ВС=119,3 мм, ОВ0=107,8 мм, ОВ’=63,4 мм Длину кривошипа находим из выражения 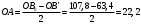 мм ммДлину коромысла находим из выражения 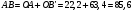 мм ммНаходим реальные размеры 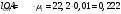 м м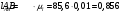 м м lСВ= СВ∙ μl= 119,3∙0,01=1,193 м Используя полученные величины отрезков геометрических параметров механизма, методом засечек, строят его кинематическую схему. Для этого на плоскости произвольно выбираем точку О (центр вращения кривошипа). Из точки О строим направляющую ползуна 5 и стойку С. Из точки О проводим окружность радиусом ОА. Окружность ОА разбиваем на 12 частей (согласно заданию) в сторону угловой скорости и получаем положение точек А (A0, A1, A2, ... A11). Из точки С строим дугу радиусом ВС. Из точек А делаем засечки на этой дуге радиусами АВ и получаем положения точек В. Для определения положения точек D из точек В проводим дугу радиусом BD и делаем засечки на направляющей ползуна 5 и получаем положения точек D. 2.2 Построение плана скоростей механизмаПостроение плана скоростей для заданного положения механизма позволяет решить одну из задач кинематического анализа, а в частности определить величины и направления линейных, относительных и угловых скоростей характерных точек и звеньев механизма Для заданного положения механизма построим план скоростей, который представляет собой пучок векторов, выполненный в определенном масштабном коэффициенте скоростей 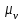 , лучи которых изображают вектора линейных скоростей характерных точек механизма, а отрезки, соединяющие вершины этих векторов, соответствуют векторам относительных скоростей звеньев. При этом построение плана основано на последовательном графическом решении векторных уравнений. , лучи которых изображают вектора линейных скоростей характерных точек механизма, а отрезки, соединяющие вершины этих векторов, соответствуют векторам относительных скоростей звеньев. При этом построение плана основано на последовательном графическом решении векторных уравнений. Рассмотрим положение 3. Так как угловая скорость ведущего звена постоянна ( ω1 = const ), то по заданной частоте вращения кривошипа определяем её величину: ω1=  с-1 с-1Находится скорость точки A: VA= 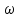 1× 1×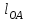 =12,57×0,222= 2,79 ( =12,57×0,222= 2,79 (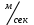 ). ).Определяется масштаб плана скоростей: 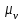 = =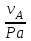 = =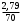 = 0,04 = 0,04 . .Запишем векторные уравнения распределения скоростей, последовательно решая которые построим план скоростей. Вектор скорости точки А представляет собой геометрическую сумму векторов скорости точки O и скорости относительного вращательного движения точки A вокруг точки O: 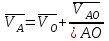 Точка O в схеме механизма является неподвижной, следовательно, модуль её скорости равен нулю ( VO =0 ). Вектор скорости VAO направлен перпендикулярно оси кривошипа, а линия действия совпадает с направлением вращения ведущего звена. Вектор скорости точки B, принадлежащей шатуну 2, представляет собой геометрическую сумму векторов скорости точки А и скорости относительного вращательного движения точки В вокруг точки А. С другой стороны вектор скорости точки B являет собой геометрическую сумму векторов скорости точки С – точки, которая принадлежит стойке и скорость которой равна 0, а также скорости относительного движения точки B относительно точки С. Система уравнений примет вид 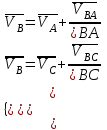 Решаем систему графически. Для этого из точки а проводим прямую, перпендикулярную звену AB, а с полюса прямую, перпендикулярную звену СB. В месте пересечения получаем точку b. Скорости равны  Вектор скорости точки D, принадлежащей шатуну 4, представляет собой геометрическую сумму векторов скорости точки B и скорости относительного вращательного движения точки D вокруг точки B. С другой стороны вектор скорости точки D являет собой геометрическую сумму векторов скорости точки D0 – точки, которая принадлежит направляющей и скорость которой равна 0, а также скорости относительного движения точки D относительно точки D0. Система уравнений примет вид 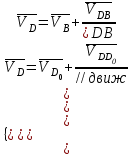 Решаем систему графически. Для этого из точки b проводим прямую, перпендикулярную звену BD, а с полюса прямую, параллельно движению ползуна 5. В месте пересечения получаем точку d. Скорости равны 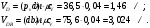 Если одному звену принадлежат несколько точек, и для двух точек этого звена векторные уравнения были составлены, то для других точек этого же звена применяется теорема подобия. Для определения положение центра масс звеньев 2,3 и 4 воспользуемся теоремой подобия 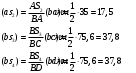 Скорости точек равны 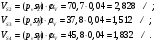 Угловая скорость шатуна AВ направлена против часовой стрелки 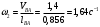 ; ; Угловая скорость коромысла ВС направлена против часовой стрелки  ; ;Угловая скорость шатуна BD направлена по часовой стрелке 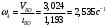 Аналогично строим планы скоростей для остальных положений механизма. Расчеты сводим в табл.1. Таблица 1 – Значение линейных и угловых скоростей механизма
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

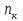 кривошипа 1 (против часовой стрелки)
кривошипа 1 (против часовой стрелки)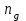 вала электродвигателя М
вала электродвигателя М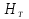 роликового толкателя 8
роликового толкателя 8