Техника безопасности. Введение в предмет. Информатика. Информация. Информационные процессы. Роль информации
 Скачать 0.72 Mb. Скачать 0.72 Mb.
|
|
Тема: Развернутая форма числа. Перевод чисел из любой системы счисления в десятичную. Цели: сформировать у учащихся навыки и умения перевода чисел из любой системы счисления в десятичную. Программно – дидактическое обеспечение: О.Л. Соколова «Поурочные разработки по информатике 10 кл.» урок 12 стр. 81, урок 13 стр. 83 Презентация Ход урока. I . Постановка целей урока. II. Проверка домашнего задания Тест для фронтального опроса (стр. 372) III. Изложение нового материала. При записи чисел значение каждой цифры зависит от ее местоположения в числе. Место для цифры называется разрядом, а количество цифр в числе – разрядностью числа. Разряды нумеруются справа налево и каждому разряду соответствует степень основания: РАЗРЯД 3 2 1 0 Название Степень Ч     ИСЛО 1 9 9 9 разряда основания ИСЛО 1 9 9 9 разряда основанияЕдиницы 100 Десятки 101 Сотни 102 Тысячи 103 Развернутая форма числа В позиционной системе счисления любое вещественное число может быть представлено в форме: Aq = +-(an-1*qn-1 + an-2 * qn-2 +….+a0* q0 + a-1*q-1 + a-2*q-2 + … + am * qm) Здесь: А – само число q – основание системы счисления ai - цифры данной системы счисления (an-2; an-1 и др.) n – число разрядов целой части числа m – число разрядов дробной части числа Пример 1: Записать в развернутом виде число А10 = 4718,63 Пример 2. Записать в развернутом виде число А8 = 7764,1 Пример 3. Записать в развернутом виде число А16 = 3AF Перевод чисел из любой системы счисления в десятичную. Правило:
Пример 4. Переведем число 11112 в десятичную систему счисления.
Пример 5. Переведем число 0,1235
Пример 6. Переведем число 16,48
IV. Решение задач. Упражнение 1. Запишите в развернутом виде следующие числа: А) А10 = 3457,78 Б) А5 = 231,44 В) А16 = Е23С,1А Г) А2 2 = 11001,101 Упражнение 2. Запишите в свернутой форме следующие числа: А) Б) Упражнение 3 Запишите в десятичной системе счисления следующие числа: А9=7688; А5 = 432,1; А3 = 120 ; А4 = 102,31 Ответ: 76889 = 566910; 432,15 = 117,210; 1203 = 1510 ; 102,314 = 2,912510 Упражнение 4. Представьте в десятичной системе счисления число 101,1, считая записанным в системах счисления от двоичной до девятеричной. Ответ: 101,12 = 5,510 101,13 = 10,310 101,14 = 17,2510 101,15 = 26,210 101,16 = 37,1610 101,17 = 50,110 101,18 = 65,12510 101,19 = 82,110 V. Закрепление изученного Выберите самостоятельно любое число из любой системы счисления и предложите соседу по парте перевести его в десятичную систему счисления. Ответы сравнить. (Работа в парах) VI. Итоги урока Оцените работу класса и назовите учащихся, отличившихся на уроке. Домашнее задание Выучить правило перевода чисел из любой системы счисления в десятичную. Знать развернутую форму записи числа. Задача №1. Сравните числа: А) 510 и 58 Ответ 510 = 58 Б) 11112 и 11118 Ответ: 11112 < 11118 Задача №2. Запишите в развернутой форме следующие числа: 7465,76210;2345,216;ACF3.B16 Задача №3 В коробке лежит 318 шар. Среди них 128 красных и 178 желтых. Докажите что здесь нет ошибки. Док-во: 318 = 2510 128 = 1010 1510+1010=2510 Задача №4 В классе 11112 девочек и 10102 мальчиков. Сколько учеников в классе. Ответ: 11112 = 1510 10102 = 1010 15+10=25 учеников. Тема: Перевод чисел из десятичной системы счисления в любую другую. Цели: сформировать у учащихся навыки и умения перевода чисел из десятичной системы счисления в любую другую. Программно – дидактическое обеспечение: О.Л. Соколова «Поурочные разработки по информатике 10 кл.» урок 14 стр. 85 Презентация Ход урока. I . Постановка целей урока. II. Проверка домашнего задания У доски проверяем решение дом. задач (выборочно) Пока учащийся у доски готовиться отвечать, остальные выполняют задание по карточкам. Задание: Заполните таблицу
Сообщите результаты теста и обратите внимание на ошибки. III. Изложение нового материала Правило перевода целых чисел из десятичной системы счисления в любую другую.
Пример 1. Перевести число 9710 в двоичную систему счисления.
Получаем 9710 = 11000012 Пример 2 Перевести число 12610 в восьмеричную систему счисления6
Получаем 12610 = 1768 Пример 3. Перевести число 18010 в шестнадцатеричную систему счисления
Получаем 18010 = В416 Правило перевода правильных дробей из десятичной системы счисления в любую другую.
Пример 4. Перевести число 0,6562510 в восьмеричную систему счисления  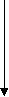 0, 65625 0, 65625*  8 8  5 25000 5 250002 00000 Получаем: 0,6562510 = 0,528 Пример 5. Перевести число 0,6562510 в шестнадцатеричную систему счисления  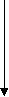 0, 65625 * 16  10(А) 50000 10(А) 50000 16 168 00000 Получаем: 0,6562510 = 0,А816 Пример 6. Перевести число 0,910 в двоичную систему счисления:  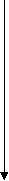 0, 9 0, 9*  2 21 8 2
2
2 
……. Этот процесс можно продолжать бесконечно. В этом случае деление продолжаем до тех пор, пока не получим нужную точность представления Получаем: 0,910 = 0,11102 с точностью до семи знаков после запятой. Правило перевода произвольных чисел. Перевод произвольных чисел, т.е. содержащих целую и дробную часть, осуществляется в два этапа. Отдельно переводится целая часть, отдельно- дробная. В итоговой записи полученного числа целая часть отделяется от дробной запятой. Пример 7. П  еревести число 18,34 в двоичную систему счисления. еревести число 18,34 в двоичную систему счисления.0, 34
 0, 68 0, 68 2 2
2
2  1 44 Получаем 18,3410 = 10010,01012 IV. Закрепление изученного. Решите задачи: №1 Переведите число 200410 в: А) в двоичную систему счисления (ответ: 111110101002) Б) в восьмеричную систему счисления (Ответ: 37248) В) в шестнадцатеричную систему счисления (Ответ: 7D416) № 2: Переведите: А) 3410 – А5 (1145) Б) 32110 – А7 (6367) В) 20110 – А3 (211103) № 3 Переведите числа из десятичной системы счисления в: А) 0,141 в пятеричную (0,03235) Б) 0,675 в троичную (0,200023) В)0,2004 в восьмеричную (0,146458) Г) 0,7982 в двоичную (0,1100112) V. Итоги урока. Оцените работу группы и назовите учащихся, отличившихся на уроке. Домашнее задание: Знать алгоритмы перевода чисел из десятичной системы счисления в любую другую. Заполните следующую таблицу:
Тема: Двоичная арифметика. Цели: продолжить знакомство учащихся с двоичной системой счисления, указать ее недостатки и преимущества использования в ВТ; сформировать навыки выполнения арифметических действий с двоичными числами Программно – дидактическое обеспечение: О.Л. Соколова «Поурочные разработки по информатике 10 кл.» урок 16 стр. 94 Презентация Ход урока. I . Организационный момент. II. Проверка домашнего задания Попросите учащихся выписать ответы на доске и разберите решение задач, вызвавших затруднение при решении III. Изложение нового материала. Из всех позиционных систем счисления особенно проста и поэтому интересна двоичная система счисления. - Чему равно основание данной системы счисления? (2) - Какой вид имеет развернутая форма записи числа Для того чтобы лучше освоить двоичную систему счисления, необходимо освоить выполнение арифметических действий над двоичными числами. Сложение: 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 10
Из примеров видно, что при сложении столбиком двух цифр справа налево в двоичной системе счисления в следующий разряд может переходить только единица. Результат сложения двух положительных чисел либо имеет столько же цифр, сколько максимальное из двух слагаемых, либо на одну цифру больше, но этой цифрой может быть только единица Складывание трех единиц: 1+1+1=10+1=11= 1+ перенос 1 в старший разряд Вычитание: Исходя из того, что вычитание есть действие, обратное сложению, запишем правило арифметического вычитания одноразрядных чисел в двоичной системе счисления: 0 – 0 = 0 1 – 0 = 1 1 – 1 = 0 10 – 1 = 1 Используя это правило, можно проверить правильность сложения вычитание из полученной суммы одного из слагаемых. При этом, чтобы вычесть в каком либо разряде единицу из нуля, необходимо «занимать» недостающее количество в соседних старших разрядах. Умножение: 0*0=0 0*1=0 1*0=0 1*1=1 IV. Закрепление изученного Решите задачи: № 1 Выполните сложение: 1)1001001+10101 (ответ:1011110) 2) 101101+1101101 (ответ:10011010) 3) 1110101+1001101 (ответ:11000010) 4) 11000,11+11010,11 (ответ:110011,1) 5) 1011011+1011011 (ответ: 10110110) 6) 1110011+1011011 (ответ:11001110) 7) 1010111+101100 (ответ: 10000011) 8) 1110110,11+1010111,11 (ответ: 11001110,1) № 2 Выполните вычитание:
V. Итог урока Оцените работу класса и назовите учащихся, отличившихся на уроке Домашнее задание Выучить правила выполнения арифметических действий в двоичной системе счисления |
