Технология решения Схемы с ЭДС. Технология решения популярно трудных задач по физике
 Скачать 404.5 Kb. Скачать 404.5 Kb.
|
|
Подготовка к ЕГЭ по физике Технология решения «популярно трудных» задач по физике Приступим к конкретному изложению методов решения физических задач с целью формирования базовых понятий у учащихся. Что имеется в виду? Приведем всего лишь один поучительный, но обстоятельный пример решения задачи № 917 из «Сборника вопросов и задач по физике» проф. П.А. Знаменского и др., задачи, ставшей для многих поколений учителей физики «популярно трудной», а один из ее методов «единственно возможным». Текст задачи:Два элемента с э.д.с. 2 В и 1,5 В и внутренним сопротивлением r = 0,5 Ом соединены параллельно. Сопротивление внешней части цепи R = 2 Ом. Н 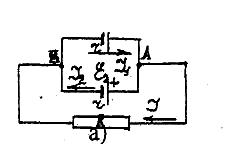  айти ток в каждом элементе и во внешней части цепи. Какова будет величина тока во внешней цепи, если второй элемент выключить? айти ток в каждом элементе и во внешней части цепи. Какова будет величина тока во внешней цепи, если второй элемент выключить?E  1= 2 B 1= 2 BE2= 1,5 B r1 = r2 = r = 0,5 Oм R = 2 Ом I1 — ? I2 — ? I — ? I — ? Рис. 1 Заданная схема Эквивалентная схема Ответ:I1 = 0,89 А; I2 = 0,11 А; I = 0,78 А; I = 0,8 А. Данную задачу решим шестью следующими методами, из которых лишь первый является наиболее конкретным и наиболее общепринятым. I. Методом узлового напряжения (условно: «обычным методом расчета»). II. Методом использования правил Кирхгофа. III. Методом узловых потенциалов. IV. Методом контурных токов. V. Методом наложения токов от различных источников. VI. Методом замены батареи эквивалентным источником тока. При решении задач промежуточные арифметические и алгебраические действия умышленно не опускаются. В связи с широким использованием вычислительной техники учащиеся самопроизвольно устраняются от полезных для них математических операций и довольно часто теряют соответствующие навыки элементарных вычислений. Так, например, при систематическом индивидуальном использовании калькуляторов учащиеся не формируют навыки даже устного счета. I. Решение методом узлового напряжения Сила тока в цепи определяется совместным действием э.д.с. элементаE1 и э.д.с. элементаE2. Для большей наглядности начертим эквивалентную схему (см. рис. в конце условия задачи). Из нее более отчетливо видно, что элементE1 следует рассматривать в качестве источника энергии, а параллельно соединенные между собой элементE2 и сопротивление R — в качестве потребителей этой энергии с напряжением между узлами их соединения UAB, т. е. на зажимах источникаE1. Таким образом, имеем систему четырех уравнений:
E1 — совершает положительную работу (разряжается — работает в режиме генератора); E2 — совершает отрицательную работу (заряжается — работает в режиме потребителя). Подставляя в общем виде значенияI1,I2, I в уравнение (1), получаем: отсюда следует, что при выполнении промежуточных действий мы имеем право подставлять численные значения величин без указания единиц их измерения. 3,5 = 2,25UAB; Следовательно: Проверка:I1 =I2 + I; 0,89 A = 0,11A + 0,78 A; 0,89 A 0,89 A. В случае отключения второго элемента I = 0, а ток во внешней цепи будет равен: Ответ:I1 0,89 А; I2 0,11 А; I 0,78 А; I= 0,8 А. Примечание.Допустим учащиеся сразу правильно не предположили, что при данном условии задачи раздваивается именно токI1, т. е. что часть его I идет через внешнее сопротивление R, а частьI2 — через второй источник против его э.д.с.E2. В итоге они неверно делают вывод, что не токI1 равен сумме токов I +I2, а ток I равен сумме токовI1 +I2. Заметим, что на первый взгляд последнее кажется более естественным. Что вносит ясность в справедливость выбора направления токов при решении данной и аналогичных задач? I1 =I1 +I2 I2 = I –I1; I2 = (0,78 – 0,89) А = –0,11 А; I2 – 0,11 А. Знак «минус» говорит о том, что действительное направление токаI2 противоположно выбранному. Таким образом, решением этой задачи удалось продемонстрировать, что базовые понятия — не информационный материал в широком смысле этого слова, не океан информационного хлама, потерявшего границы, а пример элементов знаний. Тщательно отобранных для познания окружающего мира, изюминки отшлифованного мышления. Они могут удваиваться лишь за 50, 100, 1000 лет. Этот вопрос мы продолжим анализировать во вступлениях к следующим статьям. При этом представляется целесообразным ориентировать учителя на знание многообразия методов решения задач. Последнее совсем не означает, что такая же ориентация должна быть и у учащихся. Просто учитель не должен опускаться до уровня примитивных знаний по предмету. Замечание.Учащимся, увлекающимся математическими преобразованиями, до подстановки численных значений в равенство можно предложить решить его относительно UAB в общем виде. Проделаем это. E1 – UAB)Rr2 = (UAB –E2)Rr1 + UABr1r2, E1Rr2 – UABRr2 = UABRr1 –E2Rr1 + UAB r1r2, E1Rr2 +E2Rr1 = UAB (Rr1 + Rr2 +r1r2), отсюда 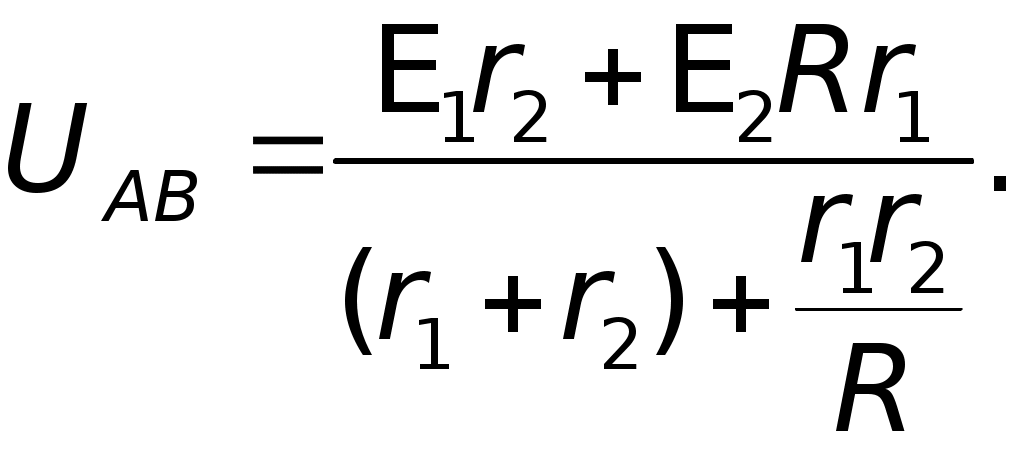 Учитывая, чтоr1=r2 = r, окончательно получаем: 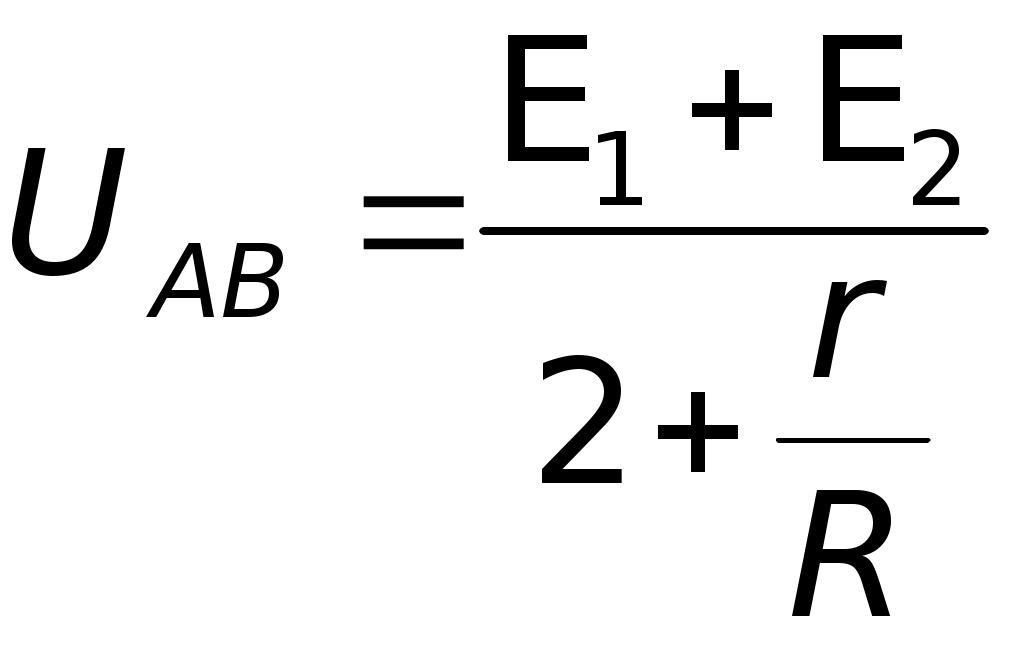 Подставляя численные значения, получаем: I2 =I1 – I; I2 = 0,89A – 0,78A = 0,11 A. Целесообразно предложить учащимся более рациональный и перспективный путь (ход) вывода формулы для расчета UAB из выше полученного равенства: Производя почлененное деление всех числителей на соответствующие знаменатели, получаем: 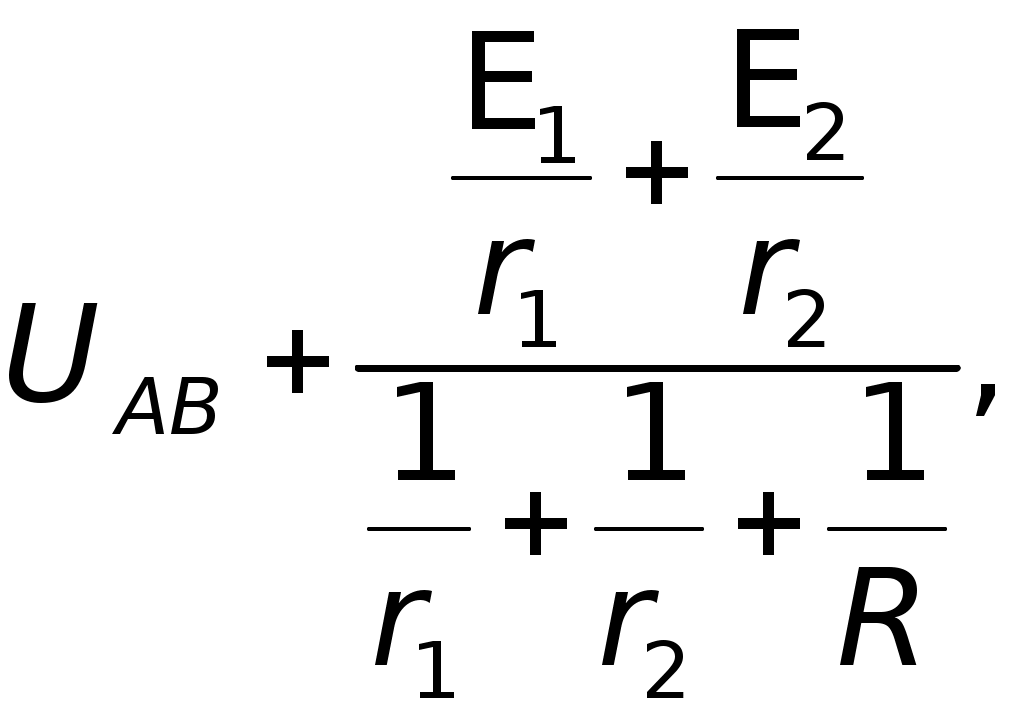  где r — внутреннее сопротивление элементов; R — внешнее сопротивление. Полученную расчетную формулу узлового напряжения на двух источниках тока и одном внешнем сопротивлении легко обобщить для п параллельно включенных источников и N сопротивлений (всех, без их разграничения на внутренние и внешние). 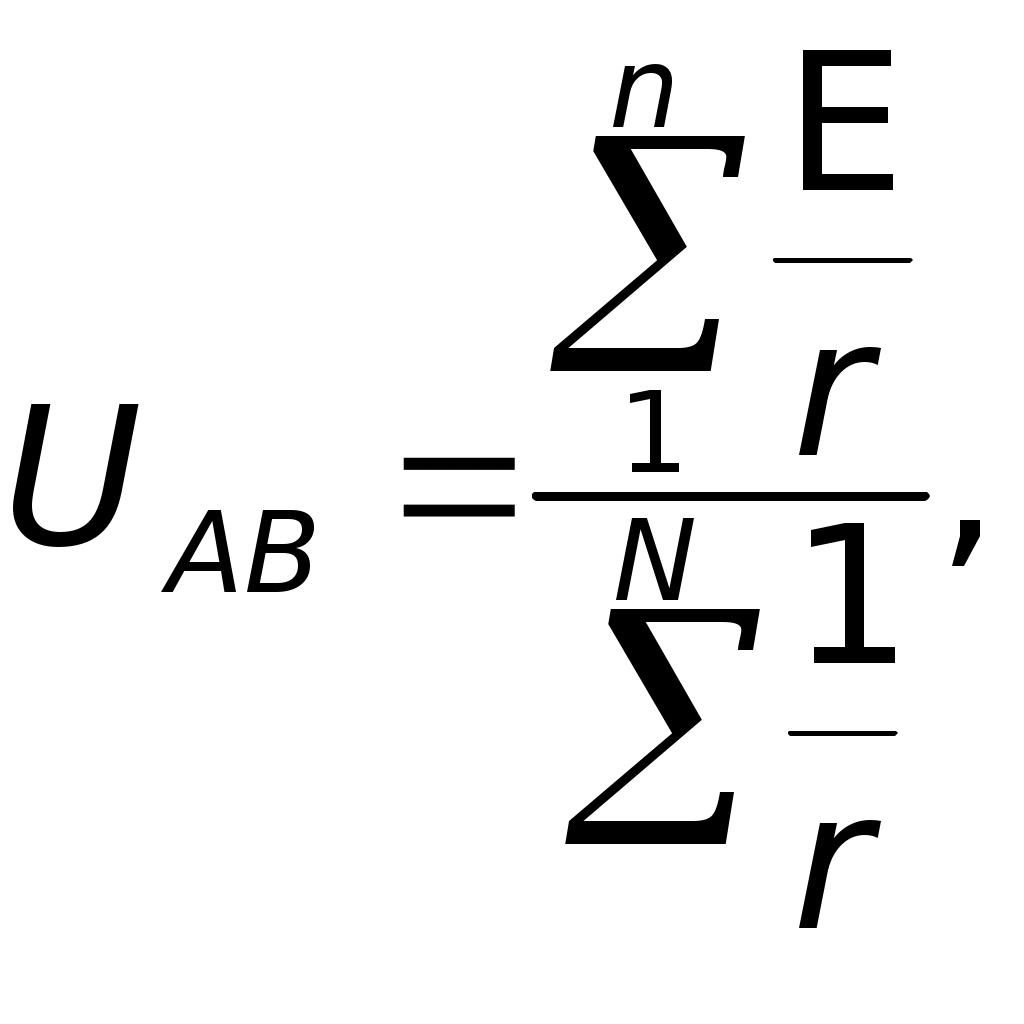 где где То есть, «узловое напряжение» равно отношению алгебраической суммы произведений э.д.с. на проводимости соответствующих ветвей к сумме проводимостей всех ветвей. Причем, если какая-либо э.д.с. направлена от узла А к узлу В, то численное значение такой э.д.с. подставляется со знаком «минус» или этот знак учитывается в явном виде в самой формуле.  Рис. «Обобщенное уравнение узлового напряжения» позволяет определить напряжение между узлами по заданным значениям э.д.с. отдельных источников тока (генераторов) и проводимостей (или сопротивлений) отдельных участков цепи (ветвей). II. Решение с помощью правил Кирхгофа Для удобства начертим эквивалентную схему.
Подставляя значениеI1 уравнения (1) в уравнения (2), получаем: E1 = (I2 + I)r1 + IR, E1 =I2r1 + I(r1 + R). Решим относительно I следующую систему уравнений: 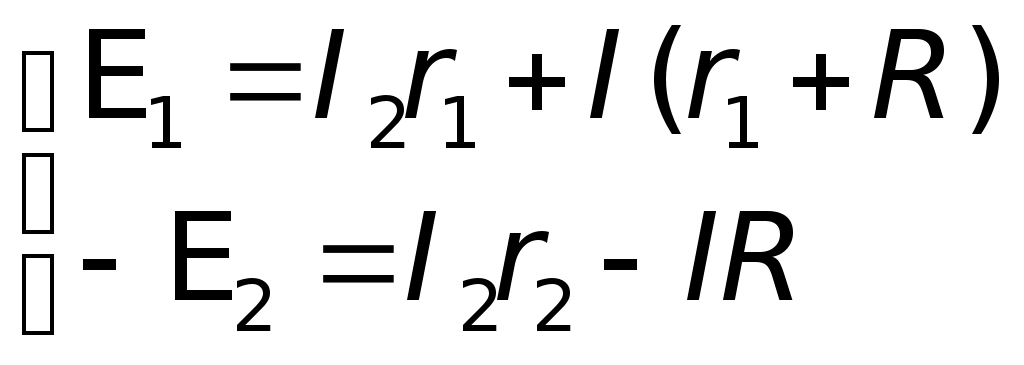 E1 +E2 = I(r + 2R), так какr1 =r2 = r Решим ту же систему уравнений относительноI2: 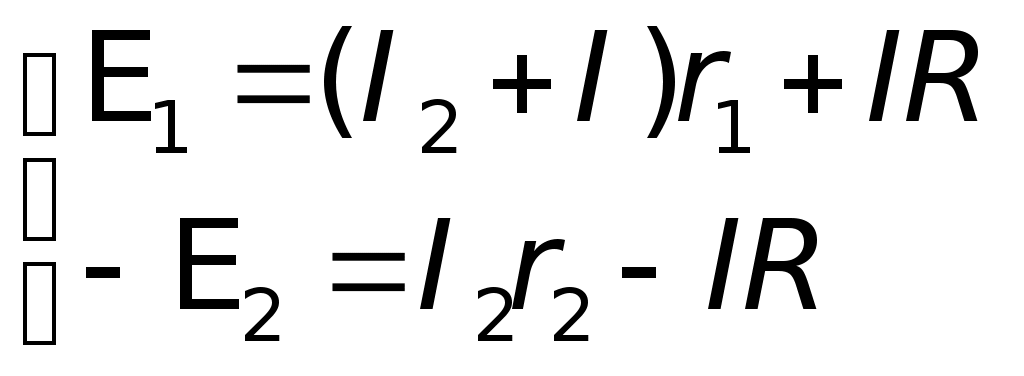 E1 –E2 =I2r1 + Ir1 +I2r2; E1 –E2 – Ir1 =I2(r1 +r2); I1 =I2 + I; I1 0,11A + 0,78A 0,89A. Ответ:I1 = 0,89A; I2 = 0,11A; I = 0,78A. III. Решение методом узловых потенциалов Метод узловых потенциалов состоит в том, что потенциал каждого узла обозначают какой-нибудь буквой, например 1, 2, 3 и т. д. Далее выбираем точку, в которой значение потенциала можно условно считать равным нулю. Это позволяет « легко перейти от использования разности потенциалов к использованию потенциала. При этом величина потенциалов будет, конечно зависеть от выбора нулевого уровня отсчета потенциалов, но разность потенциалов и картина их распределения от этого выбора не изменится. Затем составляют уравнения, выражающие такую закономерность: в случае отсутствия накопления в точках цепи зарядов сумма токов, «втекающих» в узел, равна сумме токов «вытекающих» из узла. Решив полученную систему уравнений, находят все узловые потенциалы и затем все — токи. Число неизвестных потенциалов всегда меньше на единицу числа узлов, так как потенциал одного из узлов принимается равным нулю. 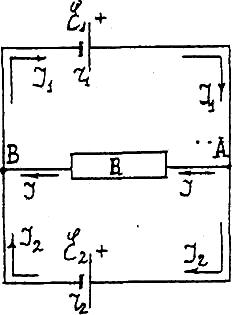 Будем считать потенциал узла В B = 0, а потенциал А равным А. Пусть токI1, текущий через элементE1 направлен от В к А, а токиI2 и I, текущие через элементE2, и сопротивление R направлен от А к В (естественно через соответствующие участки цепи). В этом случае:I1 –I2 –I3= 0; I =I2 + I. Так какr1 =r2 = r, то 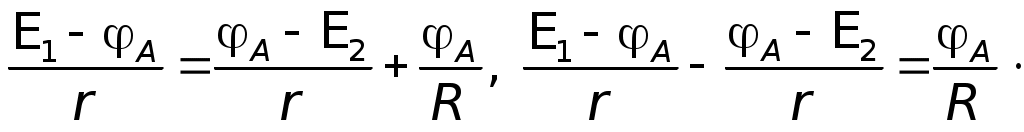 отсюда 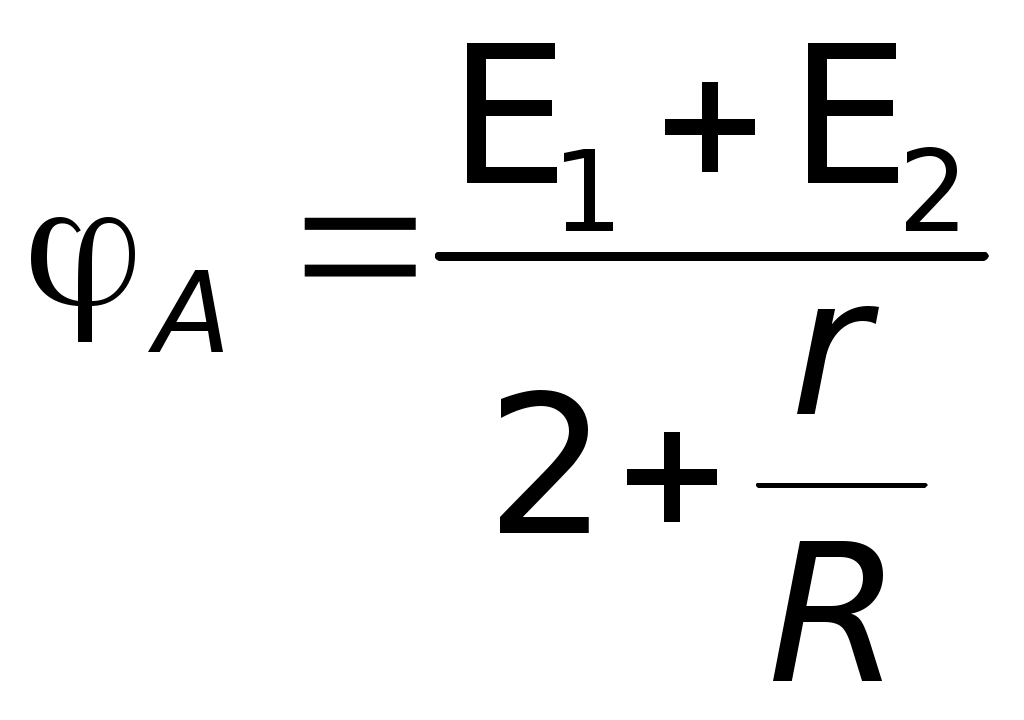 численно численно 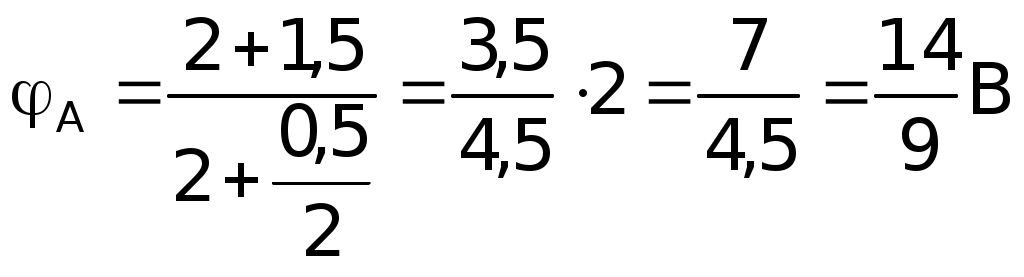 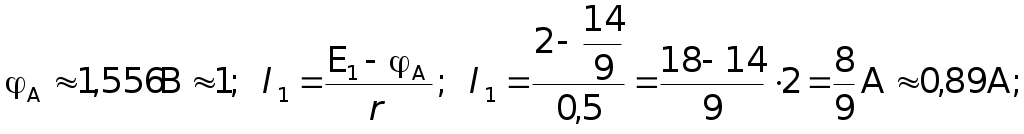 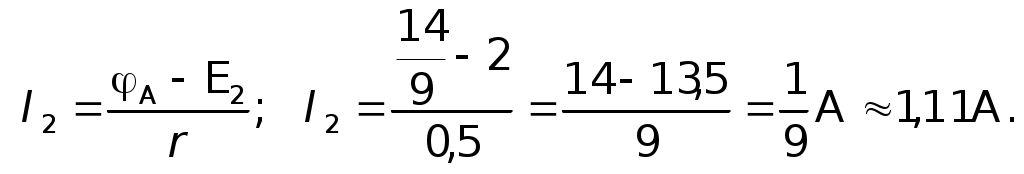  Примечание.Нередко учащимся непонятно, почему величина потенциалов зависит от выбора нулевого уровня, а разность потенциалов не зависит. В подобных случаях полезно прибегать к аналогиям. Так, например, расстояние между двумя балконами не зависит от выбора начала отсчета их высот. Аналогично разность температур по шкале Цельсия и разность соответствующих температур по шкале Кельвина будет одна и та же, хотя сами температуры будут не равны, так как 0° по шкале Цельсия и по шкале Кельвина не совпадают. Приводим конкретный пример. Пусть Очевидно, что t0 = 27 °С – 17 °С = 10 °С; T = 300К – 290К = 10К или (27 + 273)К – (17 + 273)К = 27К – 17К = 10К. Таким образом T K = t °C, 1K = 1°С. IV. Решение методом контурных токов При применении правил Кирхгофа к расчету цепей постоянного тока каждый раз приходится составлять столько уравнений, сколько неизвестных. В случае сложных цепей этих неизвестных много, в результате приходится решать систему с большим числом неизвестных. В этом случае применение метода уравнений Кирхгофа становится неэффективным. Метод контурных токов дает возможность значительно сократить (приблизительно на 50%) число уравнений для определения искомых токов. Конкретно этот метод дает возможность избавиться от необходимости составления уравнений по первому правилу Кирхгофа и ограничиться решением системы уравнений, составленных только по второму правилу Кирхгофа. Контурные токи являются величинами алгебраическими, а поэтому их положительные направления, условно задаваемые нами, обычно отмечаются кривыми стрелками в контурах.  Задаем направление контурного токаI1 по часовой стрелке, а токаI2 — против часовой стрелки. Реальные токи в случае использования этого метода решения обозначают прямыми стрелками, их направления определяют в процессе решения. В тех участках цепи, где одновременно, имеется несколько контурных токов, например, в нашем случае на сопротивлений R, результирующий ток в них равен алгебраической сумме контурных токов. Решение: Для определения контурных токовI1 иI2 составляем два уравнения, аналогичные уравнениям второго правила Кирхгофа.  Подставляя численные значения сопротивлений и решая систему данных уравнений относительно I1, получаем: 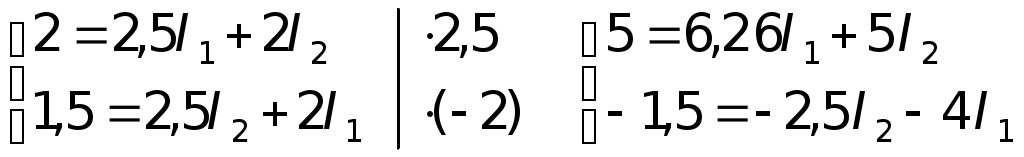 –––––––––––––––– 2 = 2,25I1 отсюда Так как через источник тока сE1 проходит один контурный токI1 и его значение получилось положительным, то реальный токI1 =I1 0,89А. Контурный токI2 определим из уравнения: E1 =I1(r1 + R) +I2R, отсюдаI2R =E1 –I1(r1 + R) 2I2 = 2 – 0,89 2,5 = 2 – 2,225 = – 0,225A, Так как через источник тока сE2 проходит так же один контурный токI2, но его значение получились отрицательным, то реальный токI2= – (+I2), I2 0,11 А. Через сопротивление R одновременно проходит два контурных тока, их алгебраическая сумма равна результирующему контурному току: I1+I2 = Ipез. Ipез. 0,89A – 0,11A 0,78 A. Так как Ipез. положительна, то реальный ток I = Ip 0,78А. Реальный ток I можно найти и по разности реальных токовI1 иI2, поскольку их направления уже были определены. I =I1 –I2; I 0,89А – 0,11А 0,78А. Ответ:I1 0,89 A; I2 0,11A; I 0,78A. V. Решение методом наложения (использования принципа суперпозиции) Известно, что ток в любом участке цепи равен алгебраической сумме отдельных токов, создаваемых в этом участке от всех э.д.с. цепи, действующих отдельно друг от друга. Напомним данные задачи и соответствующую схему.
Вначале полагаем, что в цепи действует одна э.д.с.E1, причем, все сопротивления остаются неизменными, включая внутренние сопротивления источниковr1 иr2, (на рисунках они указаны вне источников). Для такой схемы находим токораспределение. Затем повторяем расчет, полагая, что действует вторая э.д.с., а первая не действует.  Возвращаемся к первым двум схемам. Пусть ток на сопротивленииr1 равенI1, на сопротивленииr2 –I2, нa R – I. По принципу наложения: I1 = I1 — I1; I2 = I2 – I2; I = I + I, где I1, I2, I — токи, созданные в соответствующих участках первой э.д.с. E1, в предположении, что вторая э.д.с. E2 = 0; I"1, I", I" — токи, созданные второй э.д.с.E2, в предположении, что первая э.д.с.E1 = 0. Суммирование составляющих тока производится с учетом их направления. Решение: Полагая э.д.с. второго элемента недействующей находим: 1) 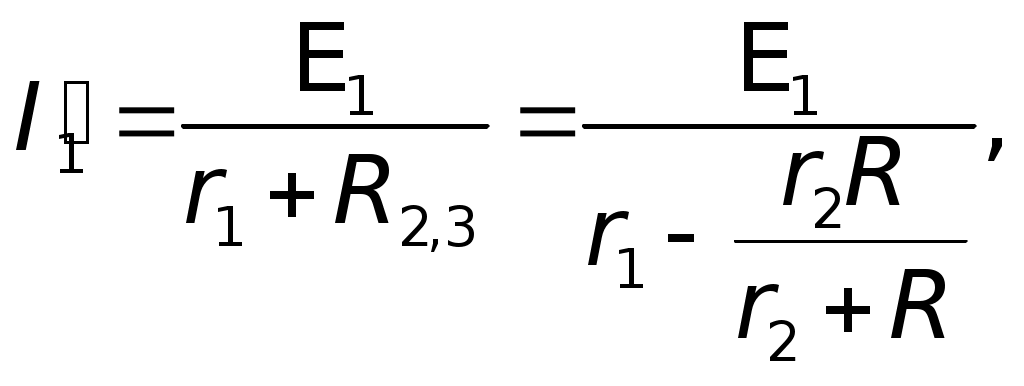 гдеR2,3 — общее сопротивление двух, параллельно соединенных сопротивлений: второгоr2и третьего — R. гдеR2,3 — общее сопротивление двух, параллельно соединенных сопротивлений: второгоr2и третьего — R. Численно: 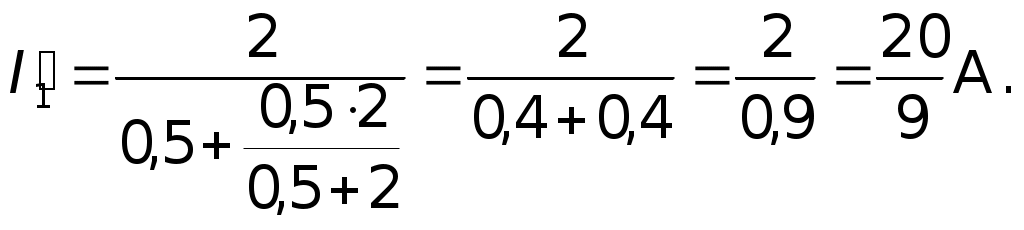 2) 3) Аналогично находим значения токов для случая, когда не действует первая э.д.с. 4) 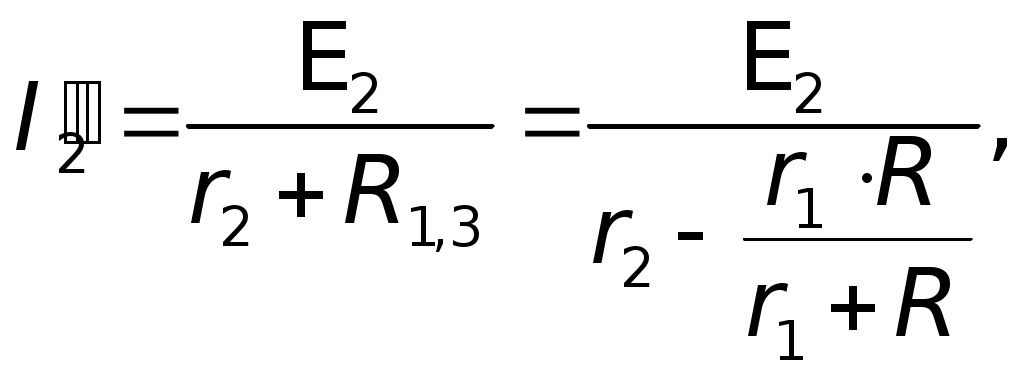 гдеR1,3 — общее сопротивление двух, параллельно соединенных сопротивлений: первого —r1и третьего R. гдеR1,3 — общее сопротивление двух, параллельно соединенных сопротивлений: первого —r1и третьего R.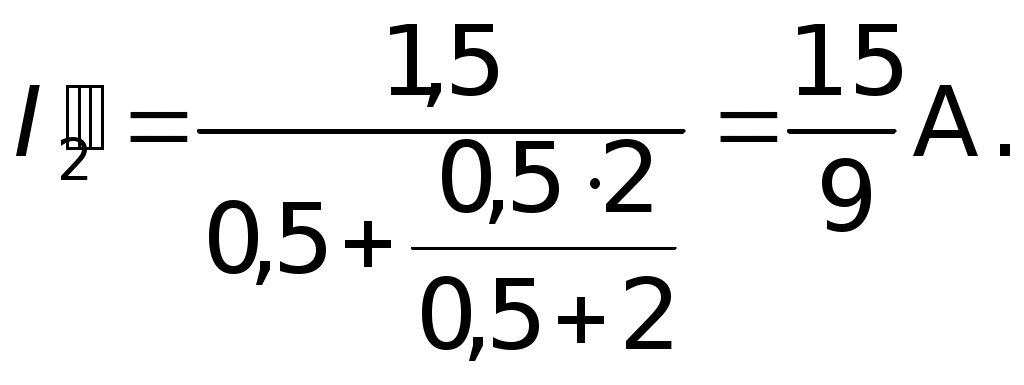 5) 6) Произведя наложение токов получаем: 7) 8) 9) Знак минус перед численным значениемI2говорит о том, что в действительности ток направлен не так, как указано стрелкой на первом и втором рисунках, реальное направление токаI2противоположно указанному. Ответ:I1 0,89A; I2 = 0,11A; I 0,78A. VI. Решение методом замены батареи элементов эквивалентным источником тока Батарею, составленную из двух и более последовательно или параллельно соединенных элементов, можно заменить эквивалентным источником тока, который обеспечит во внешней цепи такой же ток, что и батарея из нескольких элементов. Внутреннее сопротивление rэ такого источника и его э.д.с. Eэ при последовательном соединении определяются по формулам: 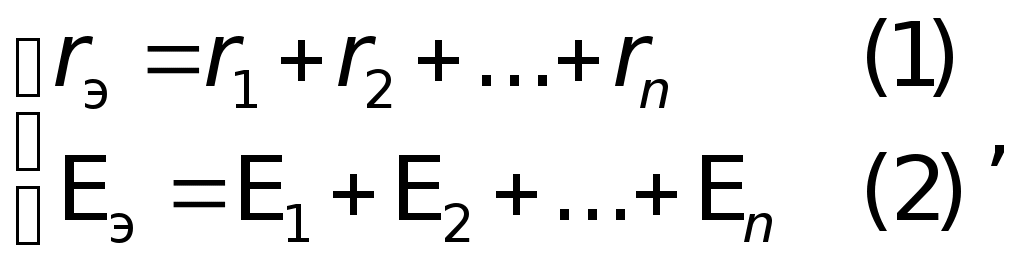 а проводимость эквивалентного источника 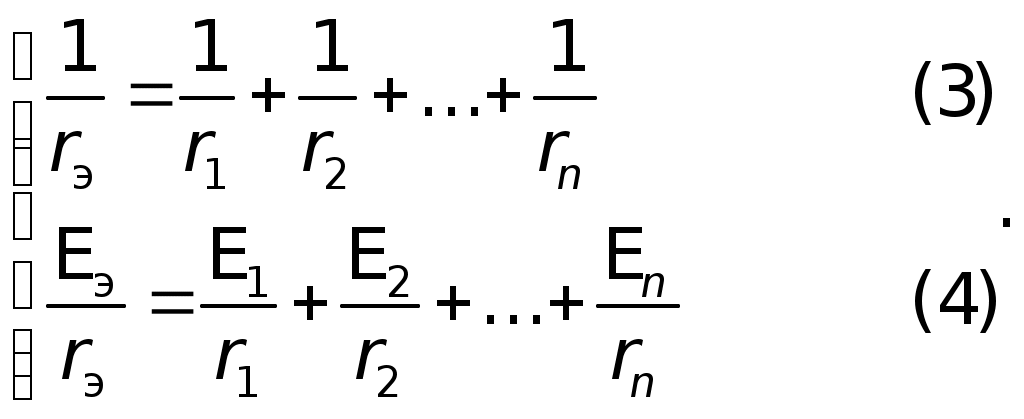 Формулы (1) и (3) для rэ и  E1 иE2 — положительны,E3 — отрицательна. Если последовательно с каким-либо элементом, например, сE1. включено сопротивление R, его можно добавить к внутреннему сопротивлению этого элемента (в нашем случае кr1), т. е. можно считать, что сопротивления R нет, а внутреннее сопротивление равно (r1+R). Заметим, что вывод формулы для расчета внутренней проводимости эквивалентного источника тока: Вывод второй формулы для определения э.д.с. эквивалентного источника Eэ также не сложен. Действительно, После подстановки получаем: Из последнего 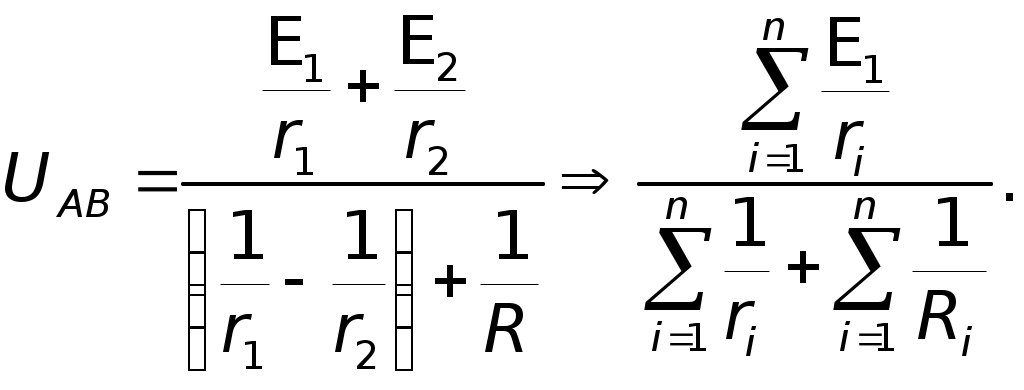 Аналогично можно записать Аналогично можно записать 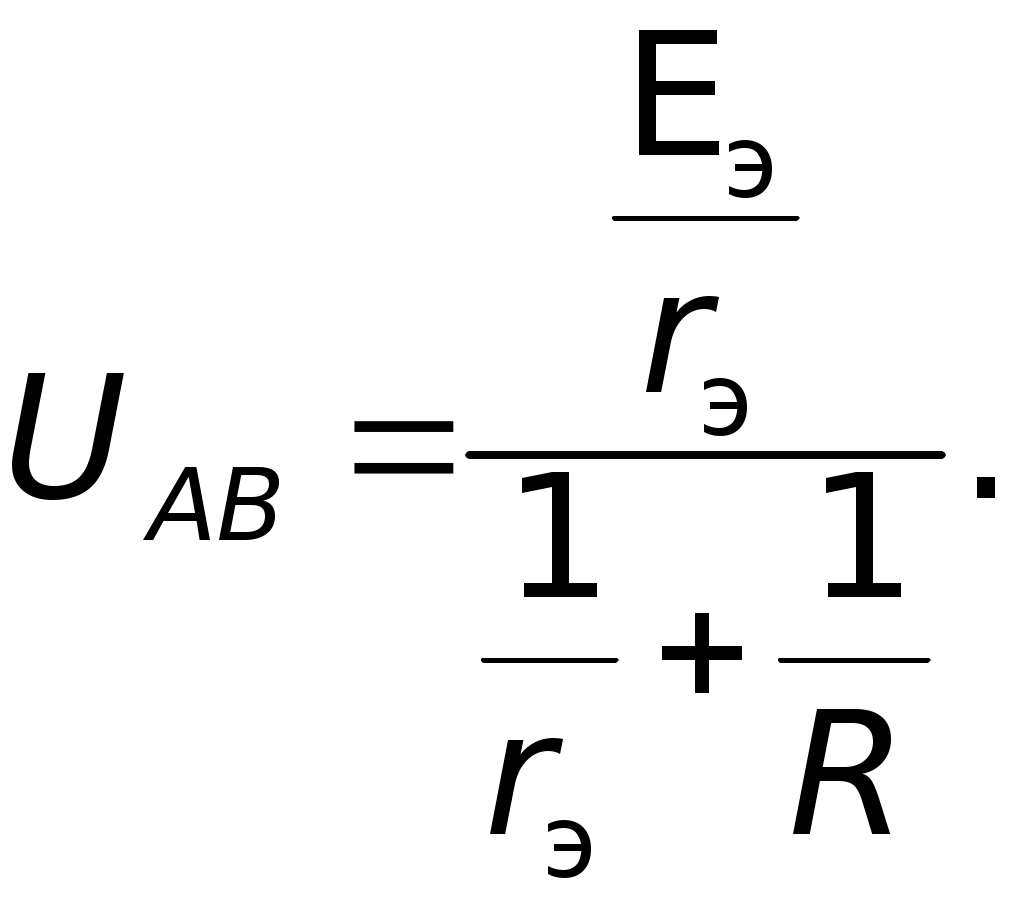 Из сопоставления следует: Обобщая для n параллельно соединенных элементов имеем: Подчеркнем еще раз в каком смысле следует понимать «эквивалентность» источника заменяющего батарею элементов. Подразумевается эквивалентность не по мощности: Подразумевается эквивалентность по сохранению во внешней цепи, независимо от ее сложности, прежних токов. Именно последнее обстоятельство позволяет рассматривать E, как э.д.с. эквивалентного источника, а rэ как его внутреннее сопротивление. (Напомним, что в rэмогут входить внешние сопротивления Ri). Приступаем к решению данной задачи указанным методом.
Eэ = (4 + 3) 0,25 B = 7 0,25 B 1,75 B.  Ответ: I = 0,78A; I1 0,89A; I2 0,11A. |