Тело, поверхность которого состоит из конечного числа плоских многоугольников, называется: четырехугольник
|
К многогранникам относятся:
параллелепипед
призма
пирамида
все ответы верны
|
Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани называется: диагональю многогранника
|
У призмы боковые ребра: общие стороны боковых граней
|
Грани параллелепипеда не имеющие общих вершин, называются: противоположными,
|
Перпендикуляр, опущенный из вершины пирамиды на плоскость основания, называется: Высотой пирамиды
|
Точки не лежащие в плоскости основания пирамиды, называются: вершины |
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется: апофема
|
У куба все грани: квадраты
|
Тело, состоящее из двух кругов и всех отрезков, соединяющих точки кругов называется: цилиндр
|
У цилиндра образующие: параллельны и равны
|
Основания цилиндра лежат в: параллельных плоскостях
|
Поверхность конуса состоит из: основания и боковой поверхности
|
Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется: диаметром
|
Всякое сечение шара плоскостью есть: круг
|
Сечение шара диаметральной плоскостью называется: большой окружностью (большим кругом)
|
Круг конуса называется: основанием
|
Основания призмы: равные многоугольники, расположенные в параллельных плоскостях
|
Площадью боковой поверхности призмы называется: сумма площадей всех боковых ее граней
|
Пересечения диагоналей параллелепипеда является его: центром симметрии
|
Вершины многогранника обозначаются: А, В, С, D ...
|
Многогранник, который состоит из двух плоских многоугольников, совмещенных параллельным переносом, называется: пирамидой
|
Если боковые ребра призмы перпендикулярны основанию, то призма является: прямой
|
Если в основании призмы лежит параллелограмм, то она является: правильной призмой
|
Многогранник, который состоит из плоского многоугольника, точки и отрезков соединяющих их, называется: конусом
|
Отрезки, соединяющие вершину пирамиды с вершинами основания, называются: боковыми ребрами пирамиды
|
Треугольная пирамида называется: тетраэдром
|
К правильным многогранникам не относится:
куб
тетраэдр
икосаэдр
пирамида
|
Высота пирамиды является: Перпендикуляр, проведенный из вершины пирамиды к плоскости основания
|
Отрезки, соединяющие точки окружностей кругов, называются: Образующими цилиндра
|
Прямая, проходящая через центры оснований называется: Осью цилиндра
|
Тело, которое состоит из точки, круга и отрезков соединяющих их, называется: Конусом
|
Тело, которое состоит из всех точек пространства, называется: Шар
|
Граница шара называется: шаровой поверхностью или сферой
|
Линия пересечения двух сфер есть: окружность
|
Сечение сферы называется: окружность
|
Грани выпуклого многогранника являются выпуклыми:
|
Боковая поверхность призмы состоит из: параллелограммов
|
Боковая поверхность прямой призмы равна: произведению периметра её основания на высоту призмы
|
К правильным многогранникам относятся: куб и додекаэдр октаэдр и икосаэдр
|
Многогранник, который состоит из двух плоских многоугольников, совмещенных параллельным переносом, называется: пирамидой
|
Если боковые ребра призмы перпендикулярны основанию, то призма является: прямой
|
Если в основании призмы лежит параллелограмм, то она является: правильной призмой
|
Многогранник, который состоит из плоского многоугольника, точки и отрезков соединяющих их, называется: конусом
|
Отрезки, соединяющие вершину пирамиды с вершинами основания, называются: боковыми ребрами пирамиды
|
Треугольная пирамида называется: тетраэдром
|
К правильным многогранникам не относится:
куб
тетраэдр
икосаэдр
пирамида
|
Высота пирамиды является: Перпендикуляр, проведенный из вершины пирамиды к плоскости основания
|
Радиус основания цилиндра равен 7, высота равна 10. Найдите площадь боковой поверхности цилиндра, деленную на пи 140
|
Геометрическая фигура, которая образована в результате вращения прямоугольника вокруг одной из его сторон: Цилиндр
|
Радиус основания конуса равен 14. Найдите площадь сечения, проведенного перпендикулярно его оси через ее середину: 49п
|
Геометрическая фигура, которая образована в результате вращения прямоугольного треугольника вокруг одного из своих катетов: Конус
|
Высота конуса равна 57, а диаметр основания-152.Найдите образуюущую конуса: 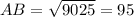
|
Тела вращения имеют: свой объем и свою площадь
|
Высота конуса равна 21, а длина образуюущей-75. Найдите диаметр основания конуса. 144.
|
Тела вращения имеют: свой объем и свою площадь
|
Диаметр основания конуса равен 56, а длина образующей-100. Найдите высоту конуса: 96
|
Площадь боковой поверхности цилиндра равна 72пи, а диаметр основания-9. Найдите высоту цилиндра: 8
|
Геометрическое место точек в пространстве, равноудаленных от некоторой заданной точки: Окружность
|
Одно их основных тел вращения: шар
|
Цилиндр называется прямым, если его образующая перпендикулярна: плоскостям оснований
|
Пирамидой называется многогранник, который состоит из … плоского многоугольника
|
Основание n-угольной пирамиды это… правильный n - угольник
|
Вершина пирамиды- это… общая точка боковых граней, не лежащая в плоскости основания
|
Боковые рёбра пирамиды – это… соединяющие вершину пирамиды с вершинами основания
|
Боковые грани n-угольной пирамиды являются… равными равнобедренными треугольниками
|
Высота пирамиды – это… Перпендикуляр, проведенный из вершины пирамиды к плоскости основания
|
У 5-ти угольной пирамиды вершин… 6
|
У 7-ми угольной пирамиды боковых граней… 7
|
У 8-ти угольной пирамиды боковых рёбер… 8
|
Плоскость, пересекающая пирамиду и параллельна её основанию, отсекает… подобную пирамиду
|
Пирамида называется правильной, если… 1) основание есть правильный многоугольник, 2) высота проходит через центр этого многоугольника.
|
Осью пирамиды называются… прямая, содержащая ее высоту
|
Апофема – это… Высота боковой грани, проведенная из ее вершины
|
Боковая поверхность правильной пирамиды равна… произведению полупериметра основания на апофему
|
Полная поверхность пирамиды состоит из… основания пирамиды и ее боковой поверхности.
|
Объём любой пирамиды равен… одной трети произведения площади основания на высоту
|
В правильной 3-х угольной пирамиде апофема равна 5м, сторона основания 3м, тогда площадь боковой поверхности… 22,5м2;
|
В правильной 4-х угольной пирамиде высота равна 9м, сторона основания 5м, тогда объём… 45м3
|
В правильной 3-х угольной пирамиде апофема равна 10м, радиус вписанной окружности 6м, тогда высота… 8м
|
Сечения n-угольной пирамиды плоскостями, проходящими через её вершину, представляют собой… треугольники
|
Полупериметр n-угольника это… сумма длин сторон n-угольника, деленная на два;
|
Объём пирамиды равен 81м3, площадь основания 27м2. Найдите высоту пирамиды. 9м
|
Сторона основания правильной пятиугольной пирамиды 2м, площадь боковой поверхности 35м2. Апофема равна… 7м
|
У усеченной пирамиды основания… подобны
|
У правильной пирамиды боковые грани являются… равнобедренными треугольниками
|
У правильной пирамиды боковые ребра… равны
|
В усеченной пирамиде боковые грани являются… трапециями
|
В основании правильной четырехугольной пирамиды лежит… квадрат
|
Сечением четырехугольной пирамиды могут быть… треугольники и четырехугольники
|
Треугольная пирамида, у которой все ребра равны называется… тетраэдром
|
 Скачать 116.5 Kb.
Скачать 116.5 Kb.