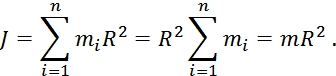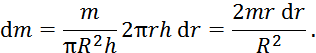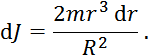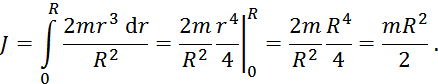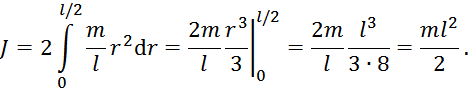ответ на вопросы. вопросы. Телом отсчета
 Скачать 1.98 Mb.
|
23.Моментом силы относительно неподвижной оси называют векторную физическую величину  , равную векторному произведению радиуса-вектора  , соединяющего по кратчайшему расстоянию ось вращения с точкой приложения силы, на вектор составляющей этой силы в плоскости, перпендикулярной оси вращения: . (6)Вектор , как это следует из (6), направлен по оси вращения в сторону, определяемую правилом правого винта. Если головку винта расположить в плоскости, образованной векторами  и , и вращать винт по направления действия силы, то движение винта покажет направление момента силы.Модуль вектора момента силы равен:  (6*)где - угол между векторами и  .24. Момент импульса тела относительно неподвижной оси вращения равен произведению момента инерции тела относительно той же оси на его угловую скорость.  (5*)Вектор  , как это следует из (5), направлен по оси вращения и совпадает с направлением вектора угловой скорости  .можно записать в виде:  , (7*)или  (8)Эта формула выражает основной закон динамики вращательного движения (или второй закон Ньютона для вращательного движения): угловое ускорение тела, вращающегося вокруг неподвижной оси, прямо пропорционально результирующему моменту всех внешних сил, действующих на тело, и обратно пропорционально его моменту инерции относительно этой же оси. 25. Для замкнутой системы момент внешних сил 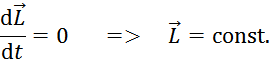 . Отсюда следует, что в этом случае: (8)Выражение (8) представляет собой закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т.е. не изменяется с течением времени. 26. В качестве количественной меры инертности тела при вращательном движении вводят понятие его момента инерции. Моментом инерцииI тела относительно неподвижной оси вращения называют скалярную физическую величину, равную сумме произведений масс элементов тела на квадраты их расстояния до этой оси:  (3)Здесь n- количество элементов, на которое разбито тело,  - момент инерции материальной точки.27. Тонкостенный цилиндр массы радиуса вращается вокруг оси , являющейся его осью симметрии. Разобьем поверхность цилиндра на малые участки массой . Толщина стенки мала и можно полагать, что вся масса (все элементы ) цилиндра находится на расстоянии от оси вращения (рис. 3.2). 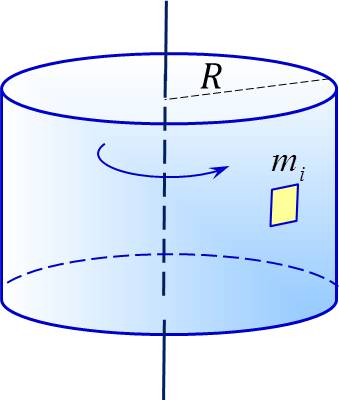 Рис. 3.2 В этом случае выражение для определения момента инерции будет иметь вид:
Сплошной однородный цилиндр массы радиуса вращается вокруг оси (рис. 3.3), являющейся его осью симметрии. 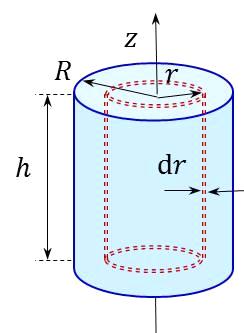 Рис.3.3 Обозначим высоту цилиндра через . Выделим внутри цилиндра тонкостенный цилиндр радиуса с толщиной стенки (на рис. 3.3 показан красным пунктиром). Масса его  , где – плотность материала; – объем тонкостенного цилиндра. Плотность материала определяется выражением:
Объем выделенного тонкостенного цилиндра равен:
а его масса
Момент инерции этого тонкостенного цилиндра (его радиус ) определяется формулой (3.4):
Следовательно, момент инерции всего цилиндра может быть найден как сумма (в данном случае интеграл) моментов инерции всех тонкостенных цилиндров указанного вида:
28. Тонкий стержень массы и длины вращается относительно перпендикулярной оси , проходящей через его середину, диаметр стержня . Выделим на стержне малый участок длины , который находится на расстоянии от оси вращения (рис.3.4). 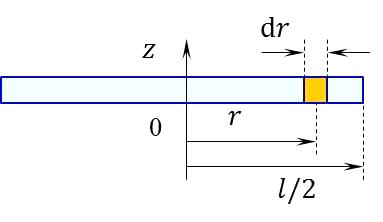 Рис. 3.4 Выделенный элементарный участок стержня можно рассматривать как материальную точку, находящуюся на расстоянии от оси вращения. Масса этой точки определяется формулой:
а ее момент инерции согласно (3.3) равен
Момент инерции всего стержня равен сумме моментов инерции элементарных участков стержня (расчет проведем для половины длины стержня и умножим результат на 2):
|
