ответ на вопросы. вопросы. Телом отсчета
 Скачать 1.98 Mb.
|
|
29. Если для какого-либо тела известен момент инерции относительно оси, проходящей через его центр инерции (центр масс), то момент инерции относительно любой оси, параллельной первой может быть найден по теореме Штейнера (рис.6). 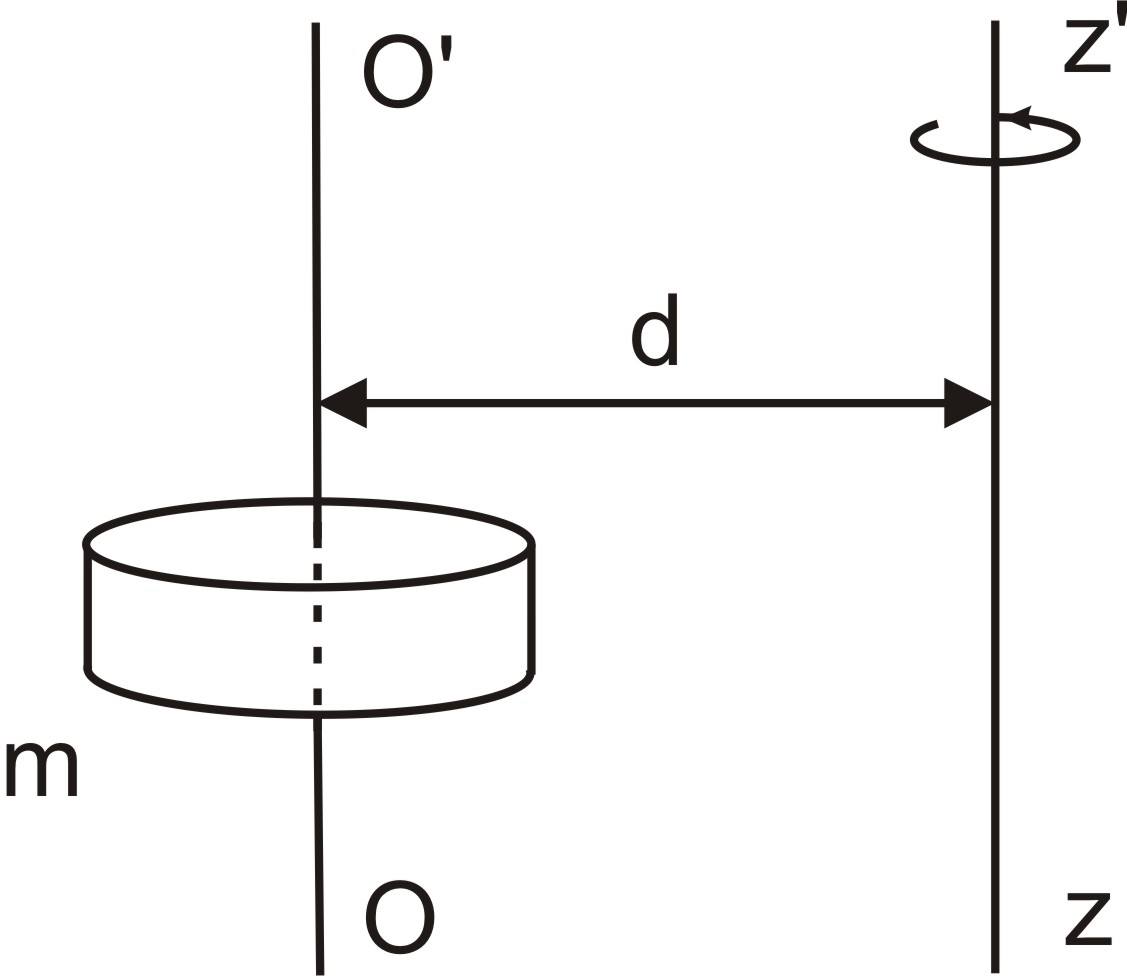 Рис.6 Теорема Штейнера: момент инерции тела I относительно любой неподвижной оси вращения равен его моменту инерции IС относительно параллельной ей оси, проходящей через центр инерции тела, сложенному с произведением массы тела на квадрат расстояния между осями:  (4)30. Если тело мысленно разбить на элементарные массы mi со скоростями 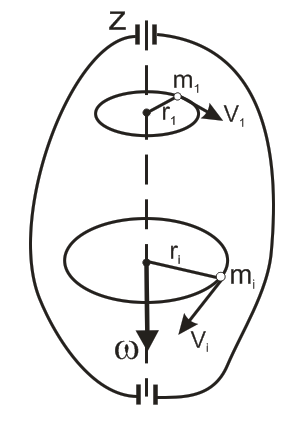 , то тогда его кинетическую энергию вращающегося твердого тела можно найти как сумму кинетических энергий этих элементов(рис.3), воспользовавшись для каждого из них формулой (1).  (3)учитывая, что угловая скорость вращения для всех точек тела одинакова:   ,где r1, r2, …, rn - радиусы вращения соответствующих элементов, выражение для Eвр. перепишем в виде: Рис. 3  , (4)где I – момент инерции вращающегося тела. Таким образом, кинетическая энергия твердого тела, вращающегося относительно неподвижной оси, равна половине произведения его момента инерции на квадрат угловой скорости. 31. Простейшим и широко используемым в технике видом сложного движения является плоское движение. 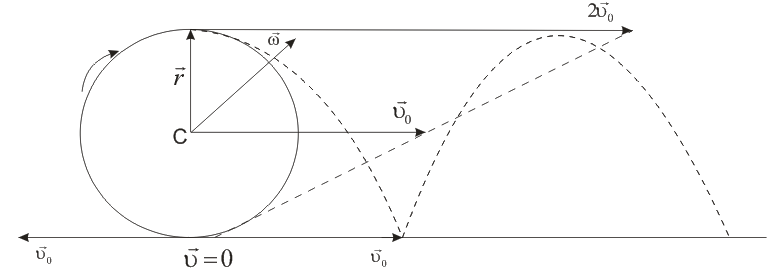 Рис. 2 Плоское движение – движение, при котором все точки тела движутся в параллельных плоскостях (так, в частности, движется колесо по дороге Рис.2). Из приведённого рисунка с очевидностью следует, что движение колеса можно разложить на поступательное со скоростью  и одновременное вращение с угловой скоростью  вокруг точки С (вектор на Рис.2 направлен за чертёж перпендикулярно его плоскости). Линейная скорость  любой точки колеса в этом случае будет складываться из скорости поступательного движения и линейной скорости  её вращения, т.е.: (1)где  радиус – вектор.Для верхней точки колеса = , и она обладает линейной скоростью 2 . Для нижней точки колеса линейная составляющая угловой скорости направлена противоположно, и эта точка колеса покоится (если нет пробуксовки). Траектория движения точки – циклоида, изображённая пунктиром. Полная энергия механического движения будет складываться из энергии поступательного движения и энергии вращения:  (5)где m- масса катящегося тела,  - скорость движения его центра инерции, Ic - момент инерции тела относительно оси и - угловая скорость вращения.32. Найдем выражения механической работы при вращательном движении. Пусть к точке тела, имеющего неподвижную ось вращения (рис. 2) в данный момент времени приложена сила F. 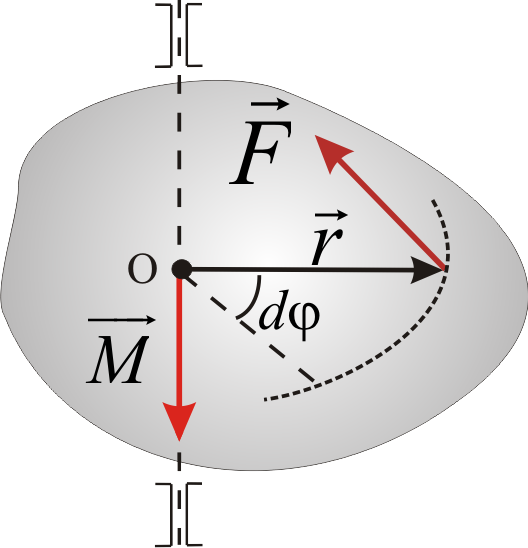 Рис. 2 Так как ось неподвижна, то точка, радиус-вектор которой обозначим через , под действием составляющей силы  будет перемещаться по окружности. За время dt она получит перемещение  , а её радиус-вектор повернётся на угол d (из-за малости d можно считать, что  ). Элементарная работа, выполненная при этом повороте, равна: ,где учтено, что dr = rd, а М =  rsin – момент силы  относительно рассматриваемой оси.Элементарная работа при вращательном движении численно равна произведению момента силы на элементарный угол поворота  . (4)При повороте на конечный угол работа  . (4/)Мощность при вращательном движении, например, мощность какого-либо двигателя, развивающего момент силы М, найдём из (4) с учётом формулы (6):  (8)cos=1 так как  и имеют одно направление.Таким образом, мощность при вращательном движении равна скалярному произведению момента силы относительно неподвижной оси, вокруг которой происходит вращение тела, на его угловую скорость. 33. Под действием момента силы происходит изменение вращательного движения, а быстрота его изменения характеризуется угловым ускорением. Следовательно, между этими величинами существует определённая связь, которая называется основным законом вращательного движения. Для установления этого закона представим тело в виде системы его элементов с массой каждого mi(рис.7). 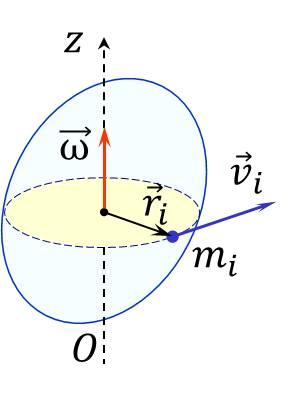 Рис. 7 На i-тый элемент тела действуют как внутренние силы (со стороны других элементов), так и внешние. Внутренние силы по третьему закону Ньютона возникают попарно и их результирующая равна нулю. Из внешних сил на вращательное движение оказывают влияние лишь проекции этих сил на плоскость, перпендикулярную к оси вращения. Результирующую  этих проекций разложим на тангенциальную и нормальную составляющие (Рис. 8)Нормальная составляющая 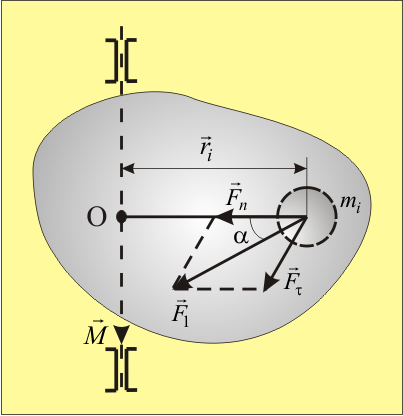 не может изменить характеристики вращательного движения, так как её направление проходит через ось вращения. Она создаёт нормальное ускорение и удерживает элементарную массу на окружности постоянного радиуса. За счёт тангенциальной составляющей  происходит изменение значения линейной скорости i-го элемента, то есть элемент приобретает тангенциальное ускорение  . Рис. 8 На основании второго закона Ньютона:  .Перейдём в записанном уравнении к характеристикам вращательного движения. Для этого: обе его части умножим на радиус вращения  , а величину  выразим через угловое ускорение  .  представим в виде  (см. рис.7). В результате будем иметь: .С учётом понятий момента силы и момента инерции, полученное равенство примет вид:  Так как момент силы и угловое ускорение, вызванное этим моментом, совпадают по направлению, то это выражение можно переписать в векторном виде:  (7)Записав такие же соотношения для всех элементов тела и векторно просуммировав их, получим:  Учитывая, что  - результирующий момент всех внешних сил, действующих на тело, а  - момент инерции всего тела.Уравнение (7) можно записать в виде:  , (7*)или  (8)Эта формула и выражает основной закон динамики вращательного движения (или второй закон Ньютона для вращательного движения): угловое ускорение тела, вращающегося вокруг неподвижной оси, прямо пропорционально результирующему моменту всех внешних сил, действующих на тело, и обратно пропорционально его моменту инерции относительно этой же оси. 34. Момент импульса тела относительно неподвижной оси вращения равен произведению момента инерции тела относительно той же оси на его угловую скорость.  (5*)Вектор  , как это следует из (5), направлен по оси вращения и совпадает с направлением вектора угловой скорости .Для замкнутой системы момент внешних сил 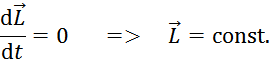 . Отсюда следует, что в этом случае: (8)Выражение (8) представляет собой закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т.е. не изменяется с течением времени. 35. Уравнение: , (7*)или (8)Эта формула выражает основной закон динамики вращательного движения (или второй закон Ньютона для вращательного движения): угловое ускорение тела, вращающегося вокруг неподвижной оси, прямо пропорционально результирующему моменту всех внешних сил, действующих на тело, и обратно пропорционально его моменту инерции относительно этой же оси. Таким образом, движение АТТ в отличие от материальной точки определяется не только действующими на него внешними силами, но и моментами этих сил. Точки приложения сил можно переносить вдоль линии их действия, так как от этого ни сумма сил, ни их моменты не изменяются. Это позволяет заменять несколько сил одной силой, эквивалентной им в отношении воздействия, оказываемого на тело. Чтобы тело осталось в покое необходимо равенство нулю как равнодействующей всех действующих на него внешних сил, так и равенство нулю результирующего момента внешних сил относительно любой оси. 36. Таблица соответствия физических величин и законов динамики поступательного и вращательного движения.
37. Колебательнымназывается всякий физический процесс, в котором значения некоторой физической величины повторяются через равные промежутки времени. Колебательной системой называется система, в которой могут происходить колебания. Свободные или собственные колебания - происходят в колебательной системе, выведенной из состояния равновесия и предоставленной самой себе. Вынужденные колебания - происходят под воздействием периодически меняющейся внешней силы. 38. Гармоническими колебаниями называются колебания, происходящие во времени по закону синуса или косинуса. График гармонического колебания x(t) показан на рис. 3.  Рис. 3 Рис. 3 Основными параметрами колебаний являются: Амплитуда А - наибольшее отклонение изменяющейся величины от среднего значения, например, для маятника - от положения равновесия (  - максимальное значение величины x(t)). В зависимости от величины, характеризующей данный колебательный процесс, амплитуда может обозначаться по-разному (xm , m , Im , Um , Em , Bmи так далее) и измеряется в тех же единицах, что и колеблющаяся величина. Период Т - промежуток времени, за который совершается одно колебание  , (2)где t – время N колебаний. Единицей измерения в системе СИ является 1 секунда: [ T ]си = 1с. Частота - количество колебаний в единицу времени  . (3)Единицей измерения в системе СИ является 1 Герц: [ ]си = 1 Гц. Скорость
Таким образом, скорость и ускорение изменяются также по гармоническому закону с той же частотой , причем амплитуда скорости равна А, а ускорения 2А. 39. В случае незатухающих гармонических колебаний изменения со временем колеблющейся величины xописываются формулой
Колебания совершаются около среднего положения (положения равновесия), соответствующего  . Величина x(t) характеризует данный колебательный процесс (например, смещение от положения равновесия, угол, ток, напряжение и так далее). 40. Математическим маятником называется идеализированная система, состоящая из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в точке. Значения собственной циклической частоты колебаний и периода колебаний математического маятника имеют вид:
 . 41. Физическим маятником называется любое твердое тело, подвешенное в точке, лежащей выше центра тяжести и способное совершать колебания. Период колебаний физического маятника зависит от момента инерции I, то есть от массы, формы и размеров тела:
l - приведенная длина, расстояние от точки подвеса до центра тяжести. Подставляя в формулы (6) моменты инерции различных тел, можно найти частоту и период колебаний различных физических маятников. 42. Пружинным маятником называется система, состоящая из шарика массы m, подвешенного на пружине, жесткостью k. Период колебаний пружинного маятника зависит от массы и жесткости пружины:  . (3)Таким образом, выведенный из положения равновесия шарик будет совершать гармонические колебания около этого положения. Частота колебаний будет тем больше, чем больше жесткость пружины k и чем меньше масса шарика m. 43. потенциальная энергия в случае гармонических колебаний равна
Кинетическая энергия в случае гармонических колебаний равна  . (9)Если колебательной системе дать начальное смещение x0=A, то она получит запас потенциальной энергии. После того как колебательную систему предоставим самой себе, она под действием квазиупругой силы начнет совершать гармонические колебания. Колебания будут сопровождаться превращением потенциальной энергии в кинетическую и наоборот. Зависимость потенциальной энергии Wn от смещения x приведена на рис. 4, а изменение кинетической и потенциальной энергии для маятника иллюстрирует рис. 5. 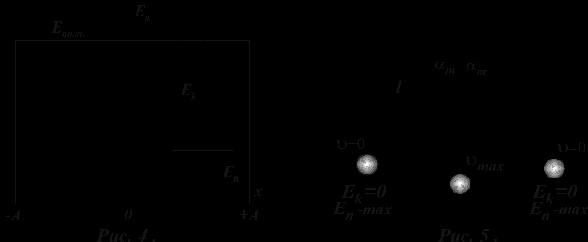 Wn Wполн. Wk Wn Wk=0 Wn-max Wk=0 Wn-max В крайних положениях колебательной системы на рис. 5 скорость и кинетическая энергия равны нулю, а потенциальная энергия максимальна и равна полной механической энергии W0. |
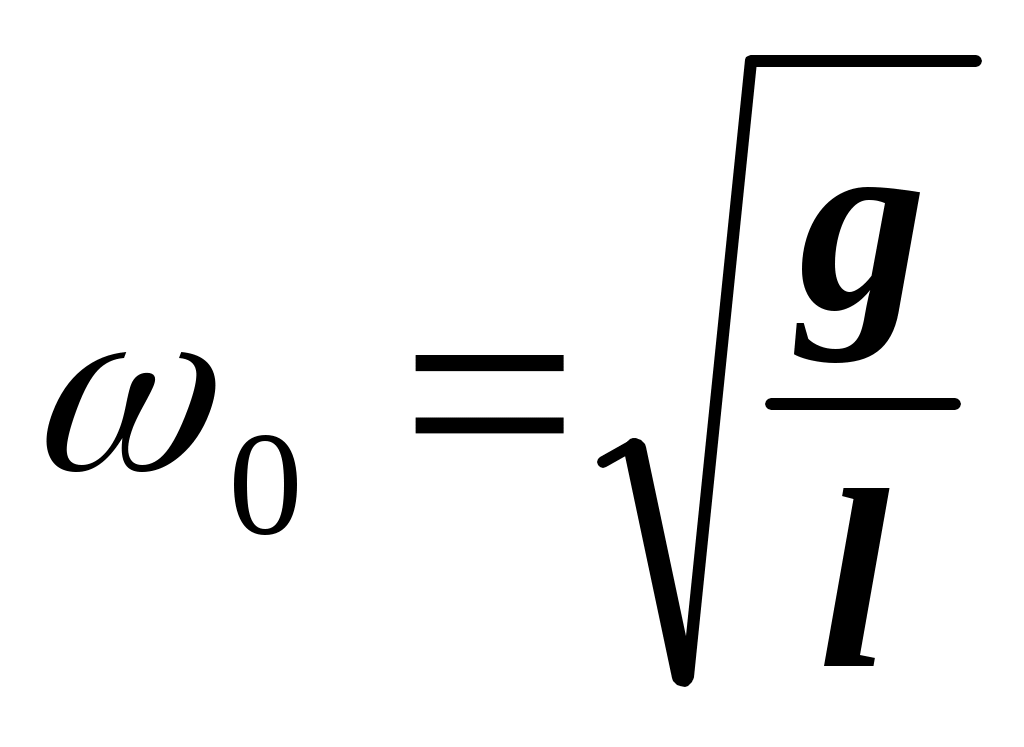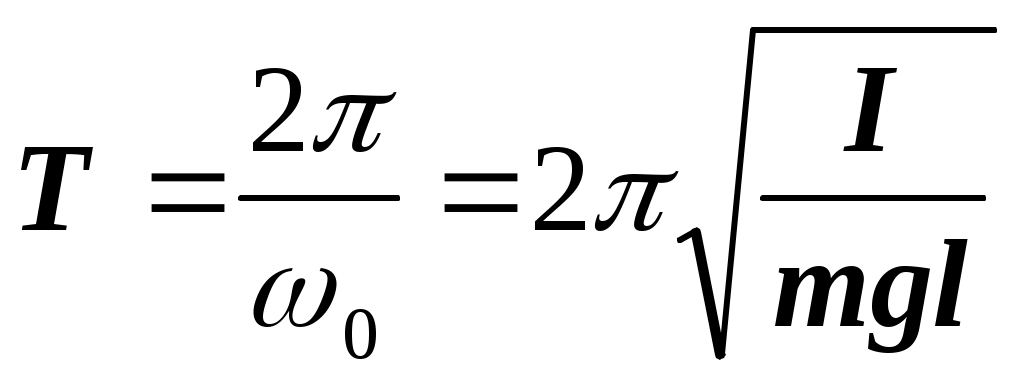
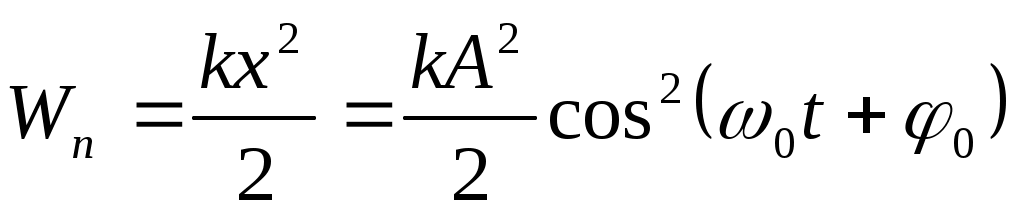перемещение
- линейная скорость
- линейное ускорение
- масса тела
- импульс
- основное уравнение
- работа
- мощность
-кинет. энергия
- линейная скорость
-линейное перемещение
-угол поворота
-угловая скорость
-угловое ускорение
- момент инерции тела
- момент силы
-основное уравнение
- работа
- мощность
- кинет. энергия
-угловая скорость
- угловое перемещение
(6)
(7)
(1)
,
.