ответ на вопросы. вопросы. Телом отсчета

• Название: Телом отсчета
• Анкор: ответ на вопросы
• Дата: 26.10.2022
• Размер: 1.98 Mb.
• Имя файла: вопросы.doc
• Тип: Документы; #755457
• страница: 1 из 6

1.

Тело, относительно которого рассматривается движение изучаемого тела, называется телом отсчета. Для описания движения с телом отсчета связывают систему координат и отсчитывающие время часы, что все вместе образуют, так называемую, систему отсчета.

Часто при рассмотрении движения тела его протяженность оказывается несущественной. Тело, размерами которого в условиях задачи можно пренебречь, называется материальной точкой. От геометрической точки материальная точка отличается тем, что ей приписывается масса тела.

Абсолютно твердым теломназывается протяженное тело, деформациями которого при решении конкретной задачи можно пренебречь. Абсолютно твердое тело при движении сохраняет свою геометрию и объем.
2.

Пусть точка движется по какой-либо криволинейной траектории так, что в момент времени t ей соответствует радиус-вектор (рис.7).

В течение промежутка времени t точка пройдет путь S и совершит перемещение . Векторную величину

(4)

определяющую быстроту перемещения точки во времени, называют вектором средней скорости движения. Направление вектора средней скорости совпадает с направлением перемещения .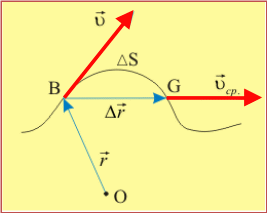


Рис. 7
Если в (3) перейти к пределу при t  0 ,то получаемое выражение представляет собой, так называемую мгновенную скорость (или просто скорость) :
(5)
Таким образом, мгновенная скорость есть векторная величина, равная первой производной радиуса – вектора движущейся точки по времени. Так как секущая БГ (рис.7) в пределе совпадает с касательной, то направлен по касательной к траектории в сторону движения.

Для решения ряда практических задач, например, при оценке времени прохождения заданного пути, пользуются числовым значением средней скорости движения на участке пути S:

(6)

В общем случае , так, S  , и только при прямолинейном движении из-за равенства средняя скорость равна модулю вектора средней скорости ( ).

Учитывая, что при t  0 путь S приближается к , для числового значения мгновенной скорости получим следующее выражение:
(7)
То есть числовое значение мгновенной скорости  равно первой производной пути по времени.
3.

Пусть некая точка переместилась за время t по траектории, показанной на (рис.5), из положения Б (с этого момента начат отсчет времени) в положение Г. Длина участка БГ, измеренная вдоль траектории, называется пройденным точкой путем S и является скалярной функцией времени: S = S(t).

Вектор

, (3)
проведенный из точки соответствующей началу рассмотрения движения, в точку, соответствующую положению тела в данный момент времени, называется перемещением.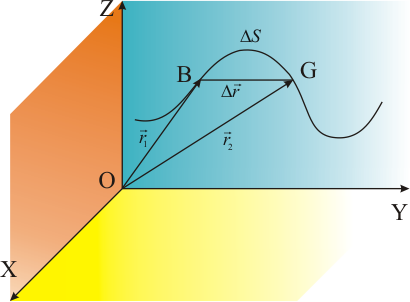



Рис.5
Очевидно, что для бесконечно малого промежутка времени dt модуль перемещения стремится к пройденному точкой пути dS. При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и модуль перемещения  за t равен пройденному пути S.
4.

В общем случае мгновенная скорость со временем может меняться. Быстроту изменения скорости характеризует ускорение.

Различают среднее ускорение
(8)
определяемое отношением приращения скорости за промежуток времени t к величине этого промежутка, и мгновенное ускорение (или просто ускорение) :

(9)
Мгновенное ускорение находится как первая производная мгновенной скорости по времени.

получим уравнение изменения скорости со временем:

(12)
получим формулу пройденного пути при прямолинейном равноускоренном движении:
(13)
Если в начальный момент в некоторой системе отсчета положение точки, движущейся вдоль оси х, характеризовалось координатой х₀, то для произвольного времени t
(14)

5.

Так как скорость, являясь векторной величиной, может меняться и по модулю, и по направлению, то и ускорение должно складываться из двух составляющих, характеризующих эти изменения в отдельности.

В случае прямолинейного движения скорость по направлению не меняется. Следовательно, ускорение имеет только одну составляющую, характеризующую изменение скорости по величине (по модулю). Эту составляющую называют тангенциальным ускорением

Для краткости назовем ее просто ускорением а. При а  0 движение равноускоренное, а  0 равнозамедленное.

6.

тангенциальное ускорение

(10)

Нормальное (центростремительное) ускорение - векторная величина, характеризующая быстроту изменения скорости по направлении.
(10^/)
Векторы нормального и тангенциального ускорения взаимно перпендикулярны, поэтому модуль полного ускорения можно представить в виде:
(11)

7.

Пусть точка Б движется по окружности радиуса (рис.11).


Рис.11
За время её радиус-вектор повернется на некоторый угол , а сама точка пройдет линейный путь

Чтобы задать не только величину поворота, но и указать в какую сторону он совершается, угол представляют в виде направленного отрезка с длиной и направлением вдоль оси вращения, определяемом правилом правого винта . Это правило требует такого направления отрезка, чтобы глядя вдоль него, мы видели поворот, совершающийся по часовой стрелке.

Векторную величину, равную первой производной угла поворота радиуса – вектора точки, проведенного из центра вращения, по времени называют угловой скоростью этой точки.
. (15)
Вектор как и направлен по оси вращения в сторону, определяемую правилом правого винта.
8.

Если , то движение точки по окружности является равномерным и его можно характеризовать периодом вращения Т - временем, за которое точка совершает один полный оборот, то есть её радиус – вектор поворачивается на угол 2. Так как промежутку времени соответствует , то , откуда
. (18)
Число оборотов, совершаемых точкой при равномерном её движении по окружности за единицу времени, называется частотой вращения:
. (19)
9.

Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени, характеризующая быстроту изменения угловой скорости:



. (20)

Из этой формулы следует, что вектор углового ускорения направлен по оси вращения в сторону элементарного приращения угловой скорости.

При ускоренном движении , и следовательно сонаправлен с (рис.12а), при замедленном - направлен в сторону, противоположную направлению (рис.12б).


Рис.12
Тангенциальная и нормальная составляющие линейного ускорения точки, движущейся по окружности, связаны с её угловыми характеристиками следующими соотношениями:

(21)
(22)
10.

Первый закон Ньютона: Существуют такие системы отсчета, относительно которых всякое тело находится в состоянии покоя или равномерного и прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит изменить его это состояние. Система отсчета, удовлетворяющая данному закону, называется инерциальной, а движение, происходящее без внешних воздействий – движением по инерции. На языке этих понятий первый закон Ньютона утверждает существование в природе инерциальных систем отсчёта и говорит, что в них движением по инерции является движение с постоянной скоростью (покой – движение с  = 0). Поэтому первый закон Ньютона называют также законом инерции.

Системы отсчёта, движущиеся относительно инерциальной системы с ускорением, называются неинерциальными (НСО).
11.

Силой называют векторную физическую величину, являющуюся мерой воздействия на тело со стороны других тел или полей, в результате, которого тело получает ускорение или (и) деформируется.

Величину силы измеряют по степени упругой деформации или по ускорению эталонного тела. Для полной её характеристики необходимо знать: численную величину, направление в пространстве и точку приложения к телу. Из опыта следует, что под действием одной и той же силы разные тела приобретают неодинаковые ускорения. Говорят, что тела обладают различной инертностью, т.е. по разному противостоят изменению состояния движения. Количественной мерой инертности тела при поступательном движении является скалярная физическая величина, называемая массой.

Связь между ускорением тела и приложенной к нему силой устанавливается вторым законом Ньютона или, как его ещё называют, основным законом динамики поступательного движения. Он утверждает: ускорение, приобретаемое телом, совпадает по направлению с действующей на него силой и равно отношению этой силы к массе тела:
(1)

или

. (2)
Если на тело действуют несколько сил, то под понимают их равнодействующую, то есть векторную сумму этих сил.
12.

Характер взаимодействия между телами определяется третьим законом Ньютона, утверждающим, что силы, с которыми действуют друг на друга взаимодействующие тела, равны по величине и противоположны по направлению (рис.1):
(6)


Рис.1
Под действием сил и тела приобретают соответствующее ускорение и . Третий закон Ньютона выполняется строго при контактном взаимодействии и при взаимодействии удалённых друг от друга покоящихся тел. Для движущихся удалённых тел, взаимодействующих посредством создаваемых ими полей, этот закон является приближённым, т.к. он предполагает мгновенное распространение взаимодействий и равенство сил в один и тот же момент времени, что в этом случае вообще говоря, не выполняется.
13.

Учитывая, что в Ньютоновской (классической) механике масса постоянна, её можно внести под знак производной и записать:
, (3)
где векторную величину
, (4)
численно равную произведению массы тела на его скорость и имеющую направление скорости, называют импульсом (количеством движения) этого тела. Формула (3) выражает более общую формулировку второго закона Ньютона: производная импульса тела по времени равна действующей на него силе. Более общей эта формулировка является потому, что она остаётся справедливой и при движении тела с большими скоростями, когда начинает проявляться зависимость массы тела от его скорости.

Из уравнения (3), характеризующего движение тела в определённый момент времени, легко получить закон изменения импульса за конечный промежуток времени t, в течение которого приложенная к телу сила постоянна:
. (5)
Величину называют импульсом силы и, следовательно, изменение импульса тела равно импульсу действующей на него силы.
14.

в системе отсчета, связанной с Землёй, на всякое тело массой m действует сила

(9)
называемая силой тяжести. Из-за суточного вращения Земли сила тяжести за исключением полюсов везде меньше гравитационной силы и изменяется с широтой: на полюсах g = 9,832 м/c², на экваторе g = 9,780 м/c². Поскольку различие значений g невелико, при приближённых расчетах полагают ускорение свободного падения постоянным и равным 9,8 м/c².

Когда тело покоится относительно поверхности Земли, сила уравновешивается силой реакции подвеса или опоры, удерживающих тело от падения ( ). По третьему закону Ньютона тело в этом случае действует на подвес или на опору с силой , т.е. с силой .

Сила , с которой тело действует на подвес или опору называется весом тела. Эта сила равна лишь в случае неподвижности тела и опоры (подвеса) относительно Земли.

Если же тело и опора движутся с некоторым ускорением , то из второго закона Ньютона подстановкой для веса тела получим выражение:

(10)
Формула (9) справедлива для опоры или подвеса любого вида и определяет вес тела в общем случае (рис. 3). Из неё видно, что для покоящегося или равномерно и прямолинейно движущегося тела (3а) его вес равен по величине силе тяжести.


Рис. 3
Однако заметим, что и приложены к разным объектам: сила тяжести приложена к самому телу, а вес к опоре или подвесу (на рис.2 тело нарисовано умыш­ленно приподнятым над опорой, чтобы показать точки приложения сил]. При свободном падении, т.е. когда , тело испытывает состояние невесомости в космических кораблях, движущихся в космосе с выключенными двигателями, в частности, в спутниках Земли.
16.

Всякое реальное тело под действием приложенных к нему сил деформируется, т.е. изменяет свою форму и размеры. В деформируемом теле возникают, так называемые упругие силы, стремящиеся восстановить его геометрию. Если после прекращения внешнего воздействия тело полностью восстанавливает свою форму и размеры, деформация называется упругой.

Опыт показывает, что для различных видов упругой деформации: растяжения, сжатия, сдвига, кручения, изгиба её величина пропорциональна возникающей упругой силе. Это утверждение носит название закона Гука, который, например, для деформации растяжения (Рис.4) должен быть записан в следующем виде:
F_упр=-kx, (11)
где x – удлинение стержня (пружины); знак минус означает,
что приращение длины стержня за счёт внешнего воздействия
происходит в сторону, противоположную действию внешней силы.


Рис.4


Коэффициент пропорциональности
(12)
(для пружины или резинового жгута – его обычно называют жёсткостью) зависит как от упругих свойств материала деформируемого тела, так и его начальной длины и площади сечения S. Величина , называемая модулем Юнга, представляет собой характеристику упругих свойств материала при продольных (растяжение и сжатие) деформациях. Аналогичная величина при деформации сдвига называется модулем сдвига G_с. Обе эти характеристики табулированы. Каждое тело имеет предел упругости при том или ином виде деформации. За пределом упругости деформация тела уже необратима и называется пластической.

Упругие деформации используются, начиная от различного рода амортизационных устройств и кончая тончайшими измерительными приборами. На пластической деформации основаны различные способы обработки металлов: штамповка, ковка, прокат и другие.

В отличие от сил упругости, возникающих при деформациях, силы трения появляются при перемещении соприкасающихся тел друг относительно друг друга и направлены по касательной к трущимся поверхностям, противодействуя их относительному смещению. При непосредственном контакте поверхностей твёрдых тел трение называется сухим. Различают три вида сухого трения: трение покоя, трение скольжения и трение качения.

Рассмотрим два соприкасающихся тела (Рис.5, где для наглядности точки приложения всех сил совмещены), одно из которых (опора) неподвижно.



Рис.5
Со стороны опоры на тело действует сила N, направленная по нормали к поверхности соприкосновения. Эта сила называется силой нормальной реакции и может быть обусловлена, например, весом тела.

При помощи внешней силы попытаемся переместить тело. Оказывается, что сдвинуть его с места удаётся только при некотором минимальном значении F₀ силы . При 0 < F <F₀ тело остаётся в покое. Следовательно, приF< F₀на тело действует сила, уравновешивающая внешнюю силу F, она автоматически принимает равное ей значение. Это и есть сила трения покоя. Величина F₀ представляет собой наибольшее значение силы трения покоя, которое определяется конкретной парой соприкасающихся тел и значением силы нормальной реакции. Если FF₀, тело начинает скользить, испытывая трение, определяемое силой трения скольжения .

Опыт показывает, что максимальная сила трения покоя и сила трения скольжения не зависят от площади трущихся поверхностей и оказываются пропорциональными величине силы нормальной реакции:
F_тр= N (13)
Безразмерный коэффициент  называется коэффициентом трения соответственно покоя или скольжения. N - сила нормальной реакции, которая можетбыть обусловлена, например, весом тела.
17.

В окружающем нас мире любое тело взаимодействует фактически с бесконечным числом окружающих его тел. Однако их силы взаимосвязи существенно различаются. Следовательно, при рассмотрении физических явлений (в том числе и механических) из всего многообразия взаимодействующих тел можно выделить некую их систему, взаимосвязь внутри которой и будет практически определять это явление.

Силы, с которыми взаимодействуют составные части системы, называются внутренними.

Внешними называются силы, с которыми вся система или отдельные её тела взаимодействуют с окружающим миром.

Замкнутой или изолированной системой тел называется система в которой внешние силы действующие на тела системы пренебрежительно малы по сравнению с внутренними силами.

Для замкнутых систем в природе действуют законы сохранения некоторых физических величин.

Для замкнутой системы (обозначим её импульс через ) имеем:

= const

Это выражение и является законом сохранения импульса:

импульс замкнутой системы сохраняется, то есть не изменяется с течением времени.
18.

Центром инерции или центром масс системы называется точка, положение которой задаётся радиусом-вектором , определяемым следующим образом:
. (16)
Здесь m_i – масса i-го тела, – его радиус-вектор; m – масса системы. Заметим, что точка с может и не совпадать ни с одним телом системы. Скорость центра масс равна производной по времени:

. (17)

Следовательно

,

то есть центр инерции движется как материальная точка с сосредоточенной в ней массой всей системы, на которую действует сила, равная векторной сумме внешних сил.
19.

Энергия – универсальная количественная мера движения и взаимодействия всех видов материи.

С различными формами движения материи связывают разные виды энергии: механическую, тепловую, электромагнитную, ядерную и др.

Полная энергия какой-либо системы определяется суммой энергий всех имеющихся в этой системе форм движения. Величина полной энергии является однозначной функцией состояния системы и не зависит от того как система приведена в данное состояние. Для замкнутой системы, как показывает опыт, полная энергия остаётся постоянной, она лишь может переходить из одного вида в другой. Этот факт является содержанием основополагающего физического закона сохранения энергии, отражающего вечность и неуничтожимость движения материи.

Изменить полную энергию системы можно только за счёт взаимодействия её с телами (телом), не входящим в данную систему. При этом система переходит из одного состояния в другое. Процесс такого перехода характеризуют величиной, называемой работой.

Работа А – это скалярная физическая величина, характеризующая процесс перехода системы из одного состояния в другое и численно равная изменению энергии системы при данном переходе:
А = W₂ – W₁, (1)
где W₁ – полная энергия системы в начальном состоянии, а W₂ – в конечном. Работа зависит не только от начального и конечного состояний системы, но и от того, как осуществляется переход, т.е. работа является функцией процесса. Если в каком-либо процессе энергия системы уменьшается (т.е. W₂  W₁), то работа, совершаемая внешними телами, отрицательна. Это значит, что сама система отдаёт внешним телам часть своей энергии и совершает над ними положительную работу. С учётом этих рассуждений энергию можно трактовать как физическую величину, определяющую потенциальную работоспособность системы.

В результате совершения работы над системой могут изменяться одна или несколько форм движения. В механике изучается механическое движение, которое, как известно, может изменяться только под действием силы (момента силы), приложенной к телу со стороны других тел. Очевидно, что при поступательном движении, чем больше величина силы, действующей вдоль направления перемещения, и чем больше само перемещение, тем значительнее изменятся механическое движение (при том же времени действия силы скорость изменится, на большую величину).

А так как изменение движения (изменение энергии) характеризуется работой, то естественно эту работу А_пост следует определить через произведение составляющей силы F_τ в направлении перемещения на величину этого перемещения (Рис.1):



Рис.1
(2)
Итак, элементарная работа при поступательном движении равна скалярному произведению вектора действующей силы на вектор перемещения.

При π/2 работа положительна; в этом случае тангенциальная составляющая силы совпадает по направлению с вектором линейной скорости движения. Если  π/2, то работа отрицательна, т.е. работа совершается против приложенной силы. При = π/2 (сила направлена перпендикулярно перемещению) механическая работа равна нулю.

Мощность N – это скалярная величина, характеризующая быстроту совершения работы и равная работе, совершаемой за единицу времени.

Различают понятия средней и мгновенной мощностей. Если за время t совершается работа А, то средняя мощность

. (5)

В пределе при t0 из (2) получим значение мгновенной (в данный момент времени) мощности:

. (6)

Мощность при поступательном движении находится из общих формул определения мощности (5), (6) с учётом выполненной работы (2)-(4). Для мгновенной мощности имеем:

(7)

Итак, мощность при поступательном движении равна скалярному произведению вектора действующей в данное время силы на вектор скорости движения.

20.

Кинетической энергией тела называют энергию, обусловленную его механическим движением и определяемую работой, которую необходимо совершить, чтобы вызвать это движение.

Если сила F действует на покоящееся тело и доводит скорость его поступательного движения до значения , то она совершая над телом работу dA, увеличивает его кинетическую энергию на dЕ. Причём dЕ = dA.

Используя скалярную запись второго закона Ньютона F

и умножая обе части равенства на величину перемещения dr, получим

.

Так как , то dЕ = md.

Интегрируя последнее выражение, найдём, что кинетическая энергия тела, движущегося поступательно со скоростью  и имеющего массу m определяется формулой:

. (9)

Потенциальная энергия – это часть полной механической энергии системы, обусловленная взаимным расположением тел или отдельных частей одного и того же тела и характером сил взаимодействия между ними.

потенциальная энергия тела в гравитационном поле Земли равна:

(10)

потенциальная энергия упругодеформированного тела

(11)
21.

Кинетическая и потенциальная энергии вместе взятые представляют собой полную механическую энергию (в дальнейшем просто механическую энергию W) системы, т.е. энергию механического движения и взаимодействия.

Е =Е_к + Е_П (12)

В результате обобщения опытных данных установлено, что в замкнутой системе тел, между которыми действуют только консервативные силы (рис.4), механическая энергия сохраняется т.е. не изменяется со временем
Е =Е_к + Е_П = соnst. (13)
Сформулированное положение представляет собой закон сохранения механической энергии.
22.

Абсолютно упругий удар – столкновение двух тел, в результате которого имеет место только упругая деформация и вся кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кинетическую энергию этих тел.

Рассмотрим столкновение шаров массами m₁ и m₂ , вращение которых отсутствует. Пусть эти шары до удара имели скорости и (Рис.5), а после удара соответственно и .


Рис.5
Законы сохранения кинетической энергии и импульса для данного случая имеют вид:




Производя в записанных формулах соответствующие преобразования, получим:





Отсюда:



Решая совместно последние два уравнения, найдём выражения для скоростей шаров после удара:

(14)

При выполнении численных расчётов нужно спроецировать соотношения (14) на ось X , вдоль которой движутся шары.

В качестве анализа полученного результата разберём несколько примеров:

1). Пусть массы шаров одинаковы ( ). Тогда из (14) следует: , т.е. шары равной массы при ударе обмениваются скоростями. Заметим, что обмен происходит не только по величине скорости, но и по её направлению. Вследствие чего движущиеся навстречу друг другу одинаковые шары отскакивают после удара в противоположных направлениях. Если до удара один из шаров был неподвижен, то в результате удара он приобретает ту же скорость (по величине и направлению), что и ударяющий шар, который в свою очередь останавливается.

2). Пусть >> . Этому соотношению масс соответствует, например, удар шара о стенку, которая может рассматриваться как шар бесконечно большой массы с бесконечным радиусом. Деля числитель и знаменатель выражения (19) на и пренебрегая членами, содержащими множитель , получаем:



Отсюда следует, что скорость стенки остаётся неизменной. Скорость же шара при неподвижной ( = 0) стенке меняет направление на противоположное. В случае движущейся стенки изменяется также величина скорости шара (возрастает на 2 , если стенка движется навстречу и убывает на 2 , если стенка "уходит" от догоняющего её шара).

Абсолютно неупругий удар – столкновение двух тел, в результате которого тела деформируясь объединяются и движутся дальше как единое целое.

Очевидно, что для этого удара закон сохранения механической энергии не выполняется, т.к. вследствие деформации происходит потеря кинетической энергии, переходящей в тепловую или другие формы энергии. Закон сохранения импульса для двух шаров в этом случае приобретает вид:



где

(15)

скорость, с которой движутся оба шара после столкновения. Если шары до удара двигались навстречу друг другу, то продолжать совместное движение, как это следует их (14), они будут в сторону, в которую двигался шар с большим импульсом. В чаcтном случае равенства масс шаров .