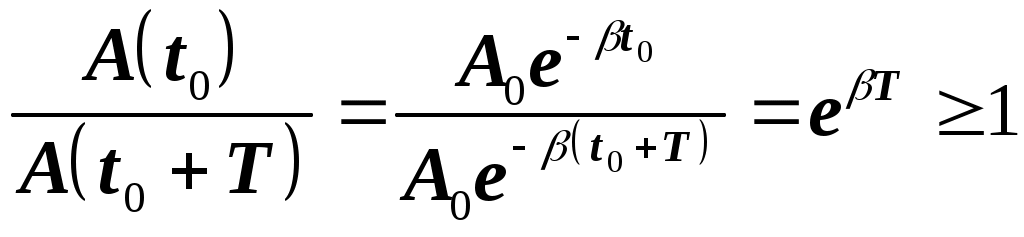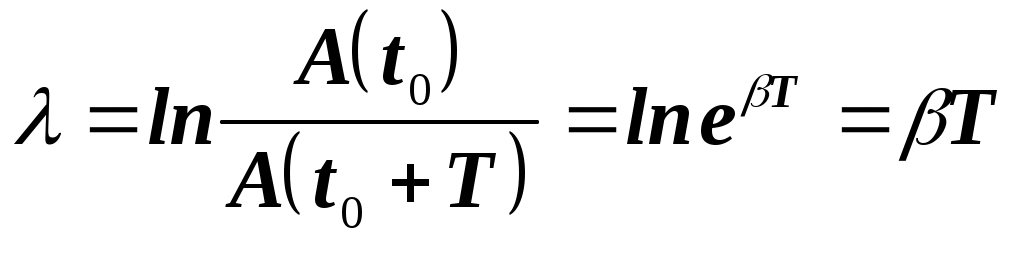ответ на вопросы. вопросы. Телом отсчета
 Скачать 1.98 Mb.
|
|
В процессе свободных незатухающих колебаний сумма кинетической и потенциальной энергии, то есть полная механическая энергия, остается постоянной: 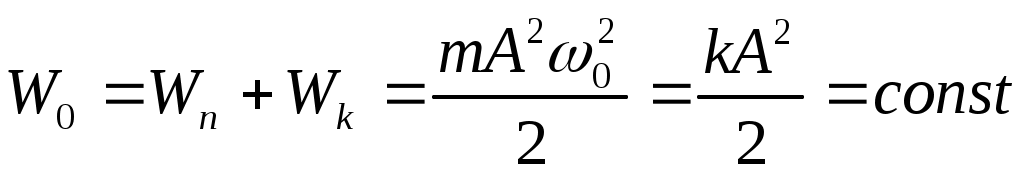 . 44. В любой реальной колебательной системе существуют силы сопротивления и трения, действие которых приводит к уменьшению энергии, запасенной в колебательной системе. Если эта убыль энергии не будет восполняться извне, как в случае свободных колебаний, то колебания будут затухать и их амплитуда будет уменьшаться. затухающая гармоническая функция
График затухающего гармонического колебания, то есть функции (11) приведен на рис. 6. 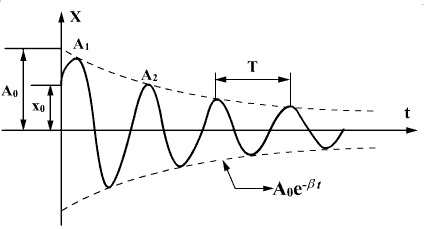 Рис. 6. Проанализируем амплитуду и частоту затухающего колебания. Амплитуда затухающего колебания- зависит от времени и уменьшается по закону экспоненты:
где A0 - амплитуда в начальный момент времени t = 0. Амплитуда уменьшается тем быстрее, чем больше коэффициент затухания , который характеризует скорость затухания колебаний. Уменьшение амплитуды во времени на рис. 6 показано штрихами. Степень затухания колебаний характеризуют и другими специальными параметрами: декрементом затухания, логарифмическим декрементом затухания и добротностью. Декрементом затухания называется отношение двух амплитуд, отличающихся на период (см. рис. 6):
Таким образом, декремент затухания - безразмерная физическая величина, характеризующая во сколько раз уменьшается амплитуда колебания за один период. Логарифмическим декрементом затухания называется безразмерная величина, равная натуральному логарифму декремента затухания:
где Т-период. 45. Вынужденные колебания - происходят под воздействием периодически меняющейся внешней силы. для установившихся колебаний является гармоническая функция времени.
Резонансом называется явление резкого возрастания амплитуды вынужденных колебаний при приближении циклической частоты вынуждающей силы к собственной частоте колебательной системы. Резонансной частотой называется частота, при которой амплитуда вынужденных колебаний максимальна.
Таким образом, резонансная частота меньше собственной частоты и зависит также от коэффициента затухания в системе. Чем больше коэффициент затухания, тем меньше резонансная частота. 46. Волновой процесс – это процесс распространения в пространстве возмущенного состояния вещества или поля, сопровождающийся переносом энергии и не связанный с переносом вещества. Волной называется процесс распространения колебаний в пространстве с конечной скоростью. Основные параметры или физические характеристики волны – скорость распространения волны , период колебаний Т, частота , длина волны . Длина волны (λ) - расстояние между двумя ближайшими точками, в которых колебания происходят в одной фазе, то есть длина волны – это расстояние , на которое распространяется волна в течение одного периода колебаний (рис. 4).  Рис. 4 (1)Скорость волны (υ) - скорость распространения возмущения в пространстве.  (2)Период волны (Т) - время, за которое волна пробегает путь, равный длине волны. Частота волны (ν) - число полных колебаний, прошедших через сечение в единицу времени. 47. Упругими волнами называется распространение механических колебаний в твердых, жидких и газообразных средах вследствие упругого взаимодействия частиц среды. Сплошной средой называется область пространства, непрерывно заполненная частицами, которые могут совершать вынужденные колебания. Частицей среды называется малый элемент ее объема, в котором содержится большое число атомов или молекул и в пределах которого изменением физических свойств среды можно пренебречь. Упругой средой называется среда, в которой возникают упругие деформации, полностью исчезающие после прекращения внешних воздействий. Наиболее распространенными являются гармонические волны, имеющие гармонический характер (колебания происходят по закону синуса или косинуса). 48. В зависимости от направления колебаний частиц среды по отношению к направлению распространения волны различают продольные и поперечные упругие волны: Продольной упругой волной называется волна, в которой частицы среды колеблются вдоль направления распространения волны. При этом возникает деформация сжатия – растяжения. Поперечной упругой волной называется волна, при распространении которой частицы среды колеблются в плоскостях перпендикулярных к направлению распространения волны. В среде возникает упругая деформация сдвига. При распространении продольной волны наблюдается периодическое сгущение и разрежение частиц среды, то есть изменение ее плотности , которое перемещается со скоростью распространения волны. При распространении поперечной волны сгущений и разрежения частиц нет, и плотность частиц не меняется. Таким образом, поперечные упругие волны могут распространяться только в твердых телах, обладающих упругостью объема и формы, а продольные - любой среде (газообразной, жидкой и твердой), обладающей упругостью объема. 49. Длина волны (λ) - расстояние между двумя ближайшими точками, в которых колебания происходят в одной фазе, то есть длина волны – это расстояние , на которое распространяется волна в течение одного периода колебаний (рис. 4). Рис. 4 (1)Скорость волны (υ) - скорость распространения возмущения в пространстве. (2)Период волны (Т) - время, за которое волна пробегает путь, равный длине волны. Частота волны (ν) - число полных колебаний, прошедших через сечение в единицу времени. 50. Геометрическими характеристиками волны являются: Волновой фронт – это геометрическое место точек, до которых дошли колебания в данный момент времени. Волновой фронт представляет собой поверхность, которая отделяет часть пространства, уже вовлеченную в волновой процесс, от области пространства, в которой колебания еще не возникли. Волновая поверхность – это геометрическое место точек, в которых колебания происходят в одной фазе. В зависимости от формы волновых поверхностей различают плоские, сферические, цилиндрические волны. 51. Наиболее распространенными являются бегущие гармонические волны, то есть волны, которые переносят в пространстве энергию. В стоячей волне нет переноса энергии. Рассмотрим гармоническую плоскую бегущую волну, распространяющуюся в однородной непоглощающей энергию среде вдоль положительного направления оси. Плотностью потока энергии называется векторная физическая величина, численно равная потоку энергии через единичную площадку, помещенную в данной точке перпендикулярно к направлению переноса энергии. Направление вектора плотности потока энергии совпадает с направлением переноса энергии.  или  (14)[j]си = 1 Вт/м2 . Из соотношения (14) следует, что полный поток энергии через некоторую поверхность S, охваченную волной, равен сумме элементарных потоков:
Через площадку S будет перенесена за время t энергия W,заключенная в объеме цилиндра с основанием S и высотой t, где - фазовая скорость волны. Эта энергия равна:  .Подставляя это выражение в плотность потока энергии, получаем:
Таким образом, вектор плотности потока энергии равен произведению объемной плотности энергии на вектор фазовой скорости волны и направлен всегда в сторону переноса энергии волной. Значение объемной плотности энергии w, а, следовательно, и вектор плотности потока энергии j для упругих и электромагнитных волн различны. Для упругих волн вектор плотности потока энергии называется вектором Умова. 52. Уравнение плоской волны имеет вид:
Здесь величина  , называется волновым числом. Это число показывает, сколько длин волн укладывается на отрезке длиной 2. Полученное уравнение справедливо как для продольной, так и для поперечной плоской волны, распространяющейся вдоль направления оси x. Нетрудно проверить что функция  , описывающая плоскую волну, является решением волнового дифференциального уравнения (3), так как при подставке в него обращает его в тождество.Волновым вектором называется произведение волнового числа на единичный вектор нормали к волновой поверхности. Этот вектор определяет направление распространения и пространственный период волны.
Если плоская волна распространяется в направлении, не совпадающем ни с одной из координатных осей x, y, z, то функция  , описывающая волну в любой точке пространства с радиус-вектором  , то есть уравнение плоской волны, распространяющейся в направлении, определяемом волновым вектором  , будет выглядеть аналогично (6):
В уравнениях плоских волн (6) и (8) амплитуда волн остается постоянной. Это справедливо в том случае, когда энергия волны не поглощается средой. 53. Основные положения молекулярно-кинетической теории вещества: 1. Все физические тела состоят из мельчайших частиц – атомов и молекул. 2. Атомы и молекулы находятся в состоянии непрерывного беспорядочного (хаотического) механического движения. 3. Свойства макроскопических тел определяются взаимодействием атомов и молекул, из которых они состоят. Моделью материального тела в молекулярной физике и термодинамике является система многих частиц, как совокупность молекул и атомов, свойства, законы движения и взаимодействия которых известны. Система многих частиц является предметом изучения молекулярной физики. Задачей молекулярной физики является вычисление усредненных, а не точных значений параметров системы многих частиц в данный момент времени. 54. Термодинамика изучает энергетические процессы в макроскопических системах многих частиц. Термодинамика не вдается в описание микроскопической картины явлений, описывая их, она опирается на извлеченные из опыта законы (начала) термодинамики. Основными термодинамическими понятиями являются понятия системы, состояния, процесса. Система – это совокупность макроскопических тел, обменивающихся энергией как друг с другом, так и с внешней средой. Система называется замкнутой, если она не обменивается энергией с внешней средой. Система называется неравновесной, если в различных точках ее объема параметры состояния системы различны. Система называется равновесной, если все параметры состояния системы имеют определенные значения, остающиеся при неизменных внешних условиях постоянными сколько угодно долго. Различают микро- и макроскопические состояния системы. Эти понятия были подробно рассмотрены при изучении темы №3 в лекции «Молекулярно-кинетические представления». Процесс – это переход системы из одного равновесного состояния в другое. |
,
.
или в векторном виде 
.
.