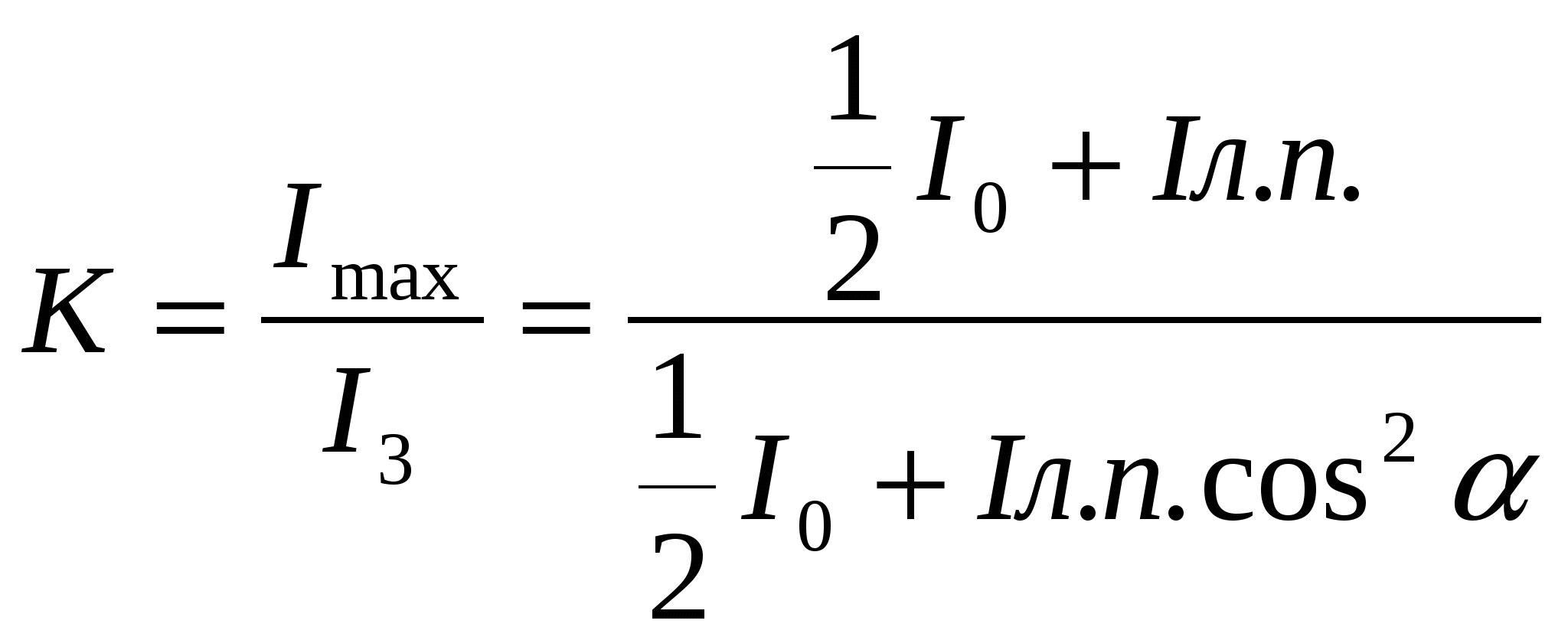Тема 1 Геометрическая оптика

• Название: Тема 1 Геометрическая оптика
• Дата: 16.04.2018
• Размер: 380 Kb.
• Имя файла: Prakt.zan.-zadachi.doc
• Тип: Задача; #41312

ОПТИКА

Тема №1 Геометрическая оптика

Задача № 1

На плоскопараллельную стеклянную пластинку толщиной d = 1см падает луч света под углом i = 60⁰. Показатель преломления стекла n.=1,73. Часть света отражается, а часть, преломляясь, проходит в стекло, отражается от нижней поверхности пластинки и, преломляясь вторично, выходит обратно в воздух параллельно первому отраженному лучу. Найти расстояние  между лучами.

Ответ: L =5,8 мм.

Задача № 2

Луч света падает под углом i на тело с показателем преломления n. Как должны быть связаны между собой величины i и n, чтобы отраженный луч был перпендикулярен к преломленному лучу?

Ответ: tg i = n

Задача № 3

Каков преломляющий угол  призмы из стекла с показателем преломления n₂ равным 1,56, если луч упавший нормально на одну ее грань, выходит вдоль другой?

Ответ:  = 39⁰52’

Задача № 4

Монохроматический луч падает нормально на боковую поверхность призмы и выходит из нее отклоненным на угол = 25⁰. Показатель преломления материала призмы для этого луча n = 1,7. Найти преломляющий угол призмы.

Ответ: = 28⁰

Задача № 5
Во сколько раз изменится длина волны света при переходе его из воды в воздух?

Ответ: длина волны в воздухе _{в воздухе} будет больше, чем длина волны в воде _{в воде} в n_воды раз (n_воды = 1,33).

Задача № 6
Длина волны зеленого света в воздухе ₀ в воздухе равна 0,55 мкм. Найти длину волны этого света в стекле, если показатель преломления стекла

n_стекла равен 1,5.
Ответ: длина волны зеленого света в стекле равна 0,37мкм.

Задача № 7

Из двух стекол с показателями преломления n₁ = 1,5 и n₂ = 1,7 сделаны две одинаковые двояко-выпуклые линзы. Найти отношение F₁/F₂ их фокусных расстояний. Какое действие каждая из этих линз произведет на луч, параллельный главной оптической оси, если погрузить линзы в прозрачную жидкость с показателем преломления n = 1,6?

Ответ: F₁/F₂ = 1,4; в жидкости первая линза будет действовать как рассеивающая, а вторая – как собирающая.

Задача №8

Радиусы кривизны поверхностей двояковыпуклой линзы: R₁ =50 см и R₂ =50см. Показатель преломления материала линзы n = 1,5.Найти оптическую силу D линзы.

Ответ: D = 2 дптр.

Задача №9

Найти фокусное расстояние F₂ линзы, погруженной в воду, если ее фокусное расстояние в воздухе F₁ = 20 м. Показатель преломления материала линзы n = 1.6.

Ответ: F₂ = 0,59 м.

Задача №10

Плоско-выпуклая линза с радиусом кривизны R=30 см и показателем преломления n = 1,5 дает изображение предмета с увеличением k =2. Найти расстояния а₁ и а₂ предмета и изображения от линзы. Дать чертеж.

Ответ: а₁ = -90 см; а₂ =180 см.

Пример решения задач :

Задача

На дно сосуда, наполненного водой до высоты h = 10 cм, помещен точечный источник света. На поверхности воды плавает круглая непрозрачная пластинка так, что ее центр находится над источником света. Какой наименьший радиус r должна иметь эта пластинка, чтобы ни один луч не мог выйти через поверхность воды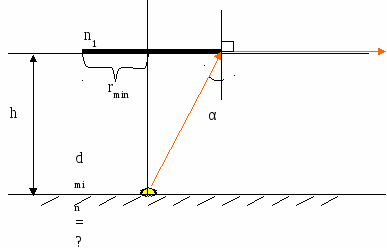





С А В
M



S

Дано:

n_{1= 1}

n_воды = 1,33

h = 10 см;

Найти:

r_min = ? Решение
Необходимо выполнить условие задачи которое заключается в том, что ни один луч не может выйти через поверхность воды.

Это условие выполняется для падающего луча SB, которому соответствует преломленный луч равный π/2 .

Запишем для точки В закон преломления :

n_воды*sinSBM = n₁*sin90⁰, откуда

sinSBM = ;

Обозначим n_воды через n₂ и запишем выражение для sinSBM как:
sinSBM = ;

Рассмотрим ∆ ASB :

Катет AB соответствует r_min ;

Катет SA соответствует h ;

tgASB = = ;

Отсюда:

r_min = h*tgASB = h* = h*;

т.к. ASB = SBM (см. чертеж), то выражение для r_min можно переписать следующим образом :

r_{min =} h*;

Подставив значение sin SBM = , получим :

r_min = ;
Ответ:
r_min = 0,114 м.

Тема №2 Интерференция

Задача №1

В некоторую точку пространства приходят когерентные лучи с геометрической разностью хода ΔS равна1,2 мкм, длина волны λ₀ которых в вакууме равна 600 нм нм. Определить, что происходит в этой точке пространства вследствие интерференции, когда лучи проходят

1. 
   в воздухе (n₁ = 1) ; 2) в воде (n₂ = 1.33); 3)в скипидаре (n₃ = 1.5)
   

Ответ:1) в воздухе будет наблюдаться максимум интенсивности;

2) в воде будет ослабление интенсивности;

3) в скипидаре будет наблюдаться максимум интенсивности.

Задача №2

На пути одного из интерферирующих лучей помещена тонкая стеклянная пластинка, вследствие чего интерференционная картина смещается на k полос (k = 5). Луч падает на пластинку перпендикулярно. Показатель преломления пластинки n₂ равен 1,6; длина волны λ равна 6,67*10^-7м. Какова толщина пластинки?

Ответ: d =5.5 мкм

Задача №3

Из воздуха на мокрое плоское стекло падает свет с длиной волны λ = 600 нм. Воду на стекле считать плоскопараллельной пленкой. При какой наименьшей толщине h_min пленки интенсивность света, наблюдаемого при отражении, достигнет максимума?

Ответ: h_min = 2.26*10^-7м.

Задача №4
Тонкая пленка с показателем преломления n= 1.5, освещается светом с длиной волны λ = 600 нм. При какой наименьшей толщине пленки интерференционные полосы исчезнут?

1. 
   в отраженном свете; 2) в проходящем свете.
   

Ответ: 1) d< λ/4n₂ ; 2) d < λ/2n₂

Задача №5

На стеклянный клин нормально его основанию падает монохроматический свет с длиной волны λ равной 0,67 мкм. Число интерференционных полос на 1см длины равно 10. Определить преломляющий угол клина.
Ответ: (θ =0,013)⁰

Задача №6

На мыльную пленку (n₂ = 1,33) падает белый свет под углом α =46⁰.При какой наименьшей толщине пленки, отраженные лучи будут окрашены в желтый цвет? (λ_желт. = 6*10^-7м.)
Ответ: d_min = 2,89*10^-7м.

Задача №7
Установка для получения колец Ньютона освещается монохроматическим светом, падающим по нормали к поверхности пластинки. Наблюдение ведется в отраженном свете. Расстояние между вторым и двадцатым темными кольцами равно 4,8мм. Найти расстояние между третьим и шестнадцатым темными кольцами Ньютона.
Ответ: l₂ =3,66мм.

Задача №8
Установка для получения колец Ньютона освещается монохроматическим светом падающим по нормали к поверхности пластинки. Радиус кривизны линзы R =15м. Наблюдение ведется в отраженном свете. Расстояние между пятым и двадцать пятым светлыми кольцами Ньютона равно 9мм. Найти длину волны λ монохроматического света.
Ответ: λ = 675нм.

Задача №9
Установка для получения колец Ньютона освещается монохроматическим светом с длиной волны λ равной 500нм, падающим по нормали к поверхности пластинки. Пространство между линзой и стеклянной пластинкой заполнено водой. Найти толщину h слоя воды между линзой и пластинкой в том месте, где наблюдается третье светлое кольцо в отраженном свете.
Ответ: h =470нм.

Задача №10
Между стеклянной пластинкой и лежащей на ней плоско-выпуклой линзой находится жидкость. Каков ее показатель преломления, если при наблюдении в проходящем свете с длиной волны λ = 600нм радиус десятого темного кольца Ньютона r₁₀ = 2,1мм. Радиус кривизны линзы равен1м. (показатель преломления жидкости меньше, чем показатель преломления стекла).
Ответ: n = 1,33

Пример решения задач

Задача 2.1
На мыльную пленку (n₂ = 1,4) падает белый свет под углом α = 52⁰. При какой наименьшей толщине пленка в проходящем свете будет казаться красной? Длина волны красного света λ. = 6,7*10^-7м.


S

Д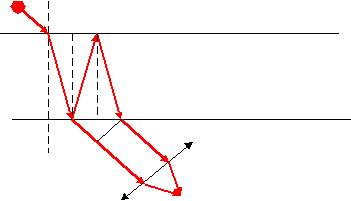
n₁
ано:

n_воды = 1,33

α
A

C

n₂

d
= 46⁰

λ_желт. = 6*10^-7м

Н
B

L
айти:


M

M


D

n₁





K


E

Решение
Луч от источника S падает на пластинку, частично преломляясь и отражаясь в точках A, B, C, и D (см. рис. 2.1).
Отражение луча в точках В и С не сопровождается потерей полуволны, т.к. в этих точках идет отражение от оптически менее плотной среды.
Следовательно, оптическая разность хода лучей SABK и SABCD
∆= 2(BC)n₂ ─ (ВК)n₁;
где n₁ – показатель преломления воздуха; n₂ – показатель преломления пленки;

BC = AB

- угол падения;

- угол преломления;

d – толщина пленки;
KBE = α, т.к. луч выходит из пластинки параллельно падающему лучу.

KDB = KBE = α, как два угла с взаимно перпендикулярными сторонами (KD _┴ BK; BM _┴ BE)

Очевидно, что АВ = BK = (DB)sinα;

(DB) = 2(BM)

(BM) найдем из ∆ BCM:

BCM = , BM = d*tg
Следовательно, BK = (DB)sin = 2(BM)sin = 2d*tgsin

В соответствии с этим
∆ = =

Учитывая, что
; sinα = ;

получаем:
∆ = = =

∆ = = 2d*
Условием максимума, т.е. условием того, что пленка будет казаться окрашенной, является
∆ = kλ

подставляя в это условие раннее выведенное выражение для оптической разности хода ∆, получим:
= kλ
Для минимальной толщины пленки k =1, так что
d_min = ;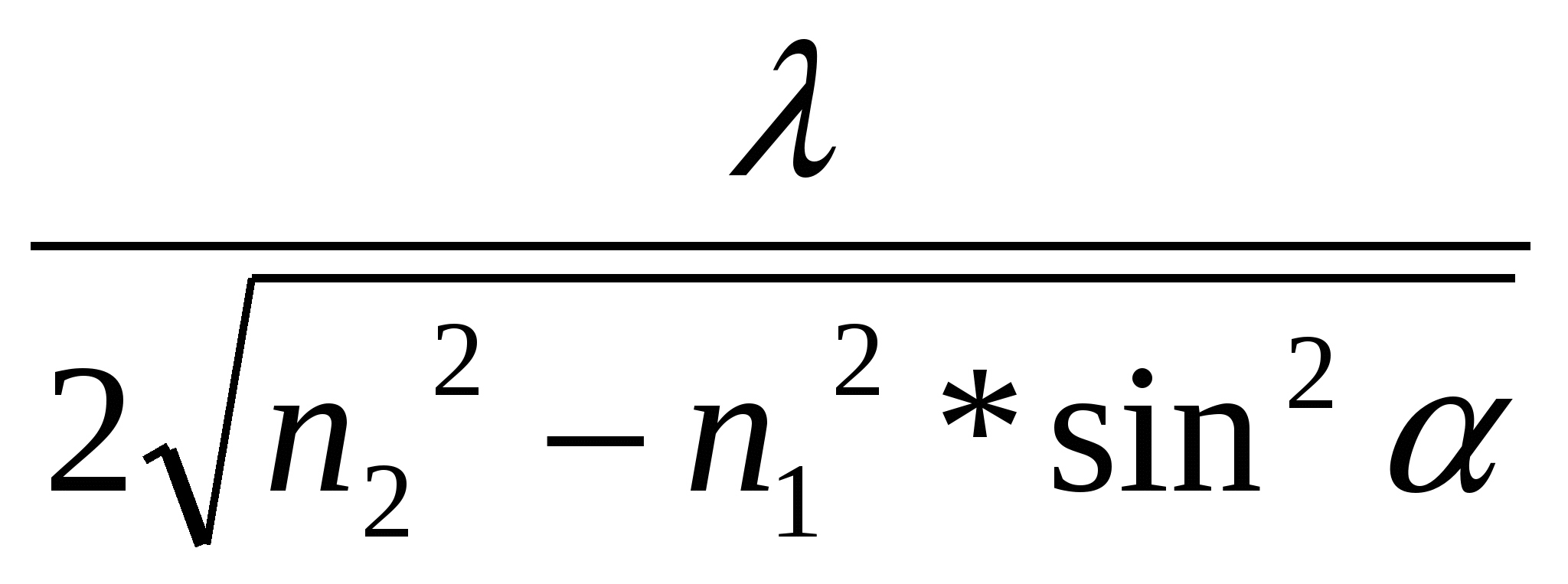
d_min = 2,89*10^-5 см.

Ответ: d_min = 2,89*10^-5 см.

Задача №2.2

К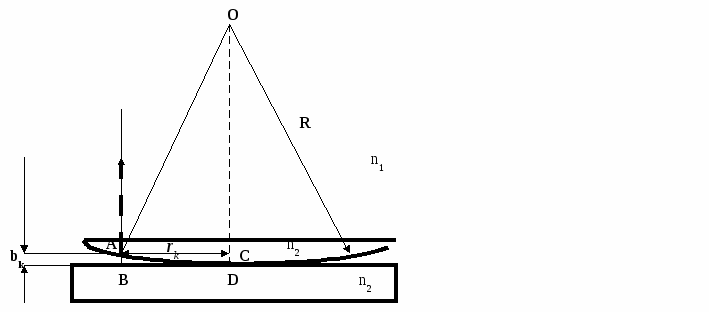
S

K
ольца Ньютона наблюдаются при отражении света от соприкасающихся друг с другом плоскопараллельной толстой стеклянной пластинки и плоско-выпуклой линзы с радиусом кривизны R = 0,96 м.. Роль тонкой пленки, от которой отражаются когерентные волны, играет воздушный зазор между пластинкой и линзой. Между светлыми кольцами Ньютона с номерами m = 7 и n = 5 расстояние l = 0,31 мм. Найти длину волны монохроматического света, падающего нормально на установку. Наблюдения проводятся в отраженном свете.

Дано:

l = 0,31 мм

n

m

R

Найти:

λ = ?

Решение
Интерференция будет наблюдаться вблизи точки D (в месте соприкосновения пластинки и линзы), т.е. там, где воздушный клин, который образуется между пластинкой и линзой имеет очень малую толщину и поэтому лучи отраженные от нижней поверхности линзы и верхней поверхности пластинки будут когерентными.

Поэтому можно считать, что свет падает по нормали к пластинки;

Для наглядности рассматриваем лучи не в (.) D, а дальше от центра – в (.)В.

Когда падающий луч доходит до точки А, лежащей на нижней поверхности линзы, то луч SA в точке А:

частично отражается, - это луч АК,

частично преломляется: - это луч AB.

На верхней поверхности пластинки в точке В луч опять частично отражается и частично преломляется, но т.к. наблюдение ведется в отраженном свете, то рассматриваем только отразившийся луч ВК.

В точке А будет наблюдаться интерференция, т.е. наложение двух когерентных лучей АК и ВК (луча отразившегося от нижней поверхности линзы АК и луча отразившегося от верхней поверхности пластинки луча ВК).
Найдем радиусы светлых колец Ньютона:
Чтобы вывести формулу для радиуса светлого кольца надо записать условие для максимума интенсивности:

(Для I_max):

Оптическая разность хода ∆ луча АК и луча ВК равна:
∆ = 2АВn_{1 + ;}

Здесь необходимо было учесть условие того, что при отражении от оптически более плотной среды происходит скачок фазы светового вектора на π, для чего необходимо прибавлять (в точке В имеется отражение от оптически более плотной среды).

В рассматриваемом случае имеются две точки в которых лучи отражаются: - это точка А, где отражается луч АК и точка В, где отражается луч ВК.

В точке А фаза светового вектора луча АК не претерпевает скачка, т.к.

луч АК проходит в линзе – в среде оптической более плотной, чем воздух, а отражается от воздуха, среды оптически менее плотной (линза имеет показатель преломления n₂ > n₁ )

В точке В происходит скачок фазы, т.к. луч ВК идет в воздухе , а отражается от линзы, среды оптически более плотной.
Определим радиус светлого кольца:

В ∆ ОАС:

катет АС – равен радиусу светлого кольца r_m

катет ОС = ОD – СD = R – AB;

АО – равен радиусу линзы R
Величина воздушного зазора АВ равна отрезку СD
По теореме Пифагора:

(АО)² = R² = (ОС)² + (АС)² = (ОD-СD)² + (AC)² = (R-AB)² + r_m = (R - b_m)² + r_m²
R² = (R - b_m)² + r_m²

R² = R² -2Rb_m + b_m² + r_m²

2Rb_m = r_m²

(слагаемым b_m² пренебречь, как величиной второго порядка малости.)

Отсюда:

b_m =

Дифракция

3.1. Дифракция Френеля

Задача№1
Найти радиус первой зоны Френеля для плоской волны, если расстояние от фронта волны до точки наблюдения 1м. Длина волны λ = 0,5мкм.
Ответ: r =0,71м.
Задача №2
Радиус r₄ четвертой зоны Френеля для плоского волнового фронта равен 3 мм. Определить радиус r₆ шестой зоны Френеля.
Ответ: r₆ = 3,69 мм.
Задача №3
Расстояние между точечным источником света с длиной волны λ = 0,63мкм и экраном равно 3,5м.Диафрагма с отверстием радиуса r находится в k раз (k=3,7) ближе к экрану, чем к источнику. В отверстии укладывается m =2 зон Френеля. Определить радиус отверстия r.
Ответ: r =0,86мм.

Задача №4
Свет от монохроматического источника (λ = 600 нм) падает нормально на диафрагму с диаметром отверстия d = 6мм . За диафрагмой на расстоянии l = 3м от нее находится экран. Какое число k зон Френеля укладывается в отверстии диафрагмы? Каким будет центр дифракционной картины на экране: темным или светлым ?
Ответ: k = 5; центр дифракционной картины будет светлым.

Задача № 5
Найти радиусы r_k первых пяти зон Френеля, если расстояние от источника света до волновой поверхности a = 1м , расстояние от волновой поверхности до точки наблюдения b = 1м. Длина волны света λ = 500 нм.
Ответ: Радиус k-й зоны r_k = ;

Подставляя числовые данные, найдем:

r₁ = 0,50 мм; r₂ = 0,71 мм; r₃ = 0,86 мм; r₄ = 1,0 мм; r₅ = 1,12 мм.

Задача № 6
Дифракционная картина наблюдается на расстоянии l от точечного источника монохроматического света с длиной волны λ = 600 нм. На расстоянии а = 0,5l от источника, помещена круглая непрозрачная преграда диаметром D = 1 см. Найти расстояние l, если преграда закрывает только центральную зону Френеля.
Ответ: l = 167 м.

Задача № 7
На диафрагму с диаметром отверстия D = 1,96 мм падает нормально параллельный пучок монохроматического света с длиной волны λ = 600 нм. При каком наибольшем расстоянии l между диафрагмой и экраном в центре дифракционной картины еще будет наблюдаться темное пятно?
Ответ: l = 0,8 м.

Задача №8
Плоская монохроматическая световая волна с интенсивностью I₀ падает нормально на непрозрачный экран с круглым отверстием. Какова интенсивность света I за экраном в точке, для которой отверстие:

а) равно первой зоне Френеля; внутренней половине первой зоны;

б) сделали равным первой зоне Френеля и затем закрыли его половину (по диаметру)?
Ответ: а) I ≈ 4I₀ ; I ≈ 2I₀;

б) I ≈ I₀;


Задача №9
Точечный источник света с длиной волны λ = 0,50 мкм расположен на расстоянии а = 100 см перед диафрагмой с круглым отверстием радиуса r равным 1,0 мм. Найти расстояние b от диафрагмы до точки наблюдения, для которой число зон Френеля в отверстии составляет k = 3.
Ответ: b = ; b = 2, 0 м.

Задача №10

Дифракционная картина наблюдается на расстоянии равном 4м от точечного источника монохроматического света (λ = 500нм). Посередине между экраном и источником помещена диафрагма с круглым отверстием. При каком радиусе R отверстия центр дифракционных колец, наблюдаемых на экране, будет наиболее темным?
Ответ: R =1мм.

Пример решения задач
Задача №3.1.1
На диафрагму с круглым отверстием радиусом r = 1 мм падает нормально параллельный пучок света с длиной волны λ = 0,5 мкм. На пути лучей, прошедших через отверстие, помещают экран. Определить максимальное расстояние b_max от центра отверстия до экрана, при котором в центре дифракционной картины еще будет наблюдаться темное пятно.
Дано:

r = 1 мм

λ = 0,5 мкм

в центре картины еще

наблюдается темное пятно

Найти:

b_max─?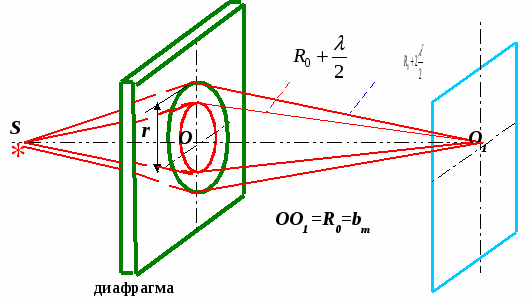



Решение

Расстояние, при котором будет видно темное пятно, определяется числом зон Френеля, укладывающихся в отверстии. Если число зон четное, то в центре дифракционной картины будет темное пятно.

Число зон Френеля, помещающихся в отверстии, убывает по мере удаления экрана от отверстия. Наименьшее число зон равно двум.

Следовательно, максимальное расстояние, при котором еще будет наблюдаться темное пятно в центре экрана, определяется условием, согласно которому в отверстии должны поместиться две зоны Френеля.

Из рисунка следует, что расстояние от точки наблюдения О на экране до края отверстия на 2 () больше, чем расстояние R₀ = b_max.

По теореме Пифагора получим
r² = (b_max + 2)² ─ b_max² = 2λb_max + λ² ;
Учтя, что λ « b_max и что членом, содержащим λ², можно пренебречь, последнее равенство перепишем в виде:
r² = 2λb_max, откуда b_max = ;
Произведя вычисления по последней формуле, найдем, что

b_max = 1 м.

Ответ: b_max = 1 м.

Задача №3.1.2
Расстояние между точечным источником света с длиной волны λ = 0,63 мкм и экраном равно l = 3,5 м. Диафрагма с отверстием радиуса r находится в

k = 3,7 раз ближе к экрану, чем к источнику. В отверстии укладывается m = 2 зон Френеля.

Определить радиус отверстия r.

Дано:

λ = 0,63 мкм

l = 3,5 м

k = 3,7

m 2

Найти

r_max = ?


Решение

a+b =l (1)

(2)

r₀ = (3)
Из уравнения (2)

a = kb

Подставим это значение а в уравнение (1):

kb+b = l

b(k+1) = l

b = ; следовательно а = kb = ;

ab = ;

a+b = l

Подставим значение ab и a+b в уравнение (3), получим:

r₀ = = ;

Подставив числовые значения, получим:

r₀ = 0,86 мм.

3.2 Дифракция Фраунгофера
Задача №1
Свет с длиной волны λ = 0,50 мкм падает на щель ширины b = 10 мкм под углом θ₀ = 30⁰ к ее нормали. Найти угловое положение первых минимумов, расположенных по обе стороны от центрального фраунгоферова максимума.

Углы θ. и угол дифракции φ лежат по разные стороны от нормали.
Ответ: Для k = +1 и k = -1 углы θ равны соответственно 33⁰ и 27⁰.

Задача №2
Чему равна постоянная дифракционной решетки, если для того чтобы увидеть красную линию (λ_кр. = 0,7 мкм) в спектре третьего порядка, зрительную трубу пришлось установить под углом α = 48⁰36’ к оси коллиматора?

Какое число штрихов нанесено на 1 см длины этой решетки?

Свет падает на решетку нормально.
Ответ: n = 3570

Задача №3
На дифракционную решетку в направлении нормали к ее поверхности падает монохроматический свет. Период решетки равен 2 мкм. Дифракционный максимум какого наибольшего порядка дает эта решетка в случае красного

(λ_кр. = 0,7 мкм) и фиолетового (λ_ф. = 0,45 мкм) света?
Задача №4

1. 
   Какое наименьшее число штрихов должна содержать решетка, чтобы в спектре первого порядка можно было разделить две желтые линии натрия с длинами волн λ₁ = 589нм и λ₂ = 589,6нм?
   
2. 
   Какова длина такой решетки, если постоянная решетки d =10 мкм.
   
3. 
   Какое число штрихов укладывается на 1см длины решетки?
   

Ответ: 1) N = 982;

2. 
   L = 9,8 мм.;
   
3. 
   n_l = 1000 (штрихов на 1см длины решетки).
   

Задача №5

На дифракционную решеткунормально падает пучок света от разрядной трубки наполненной гелием. На какую линию в спектре третьего порядка накладывается красная линия гелия (λ₁ = 6,7*10^-7м) спектра второго порядка?

Ответ: λ₂ = 4,42*10^-7м.

Задача №6
Дифракционная решетка содержит 200 штрихов на 1мм длины решетки. На дифракционную решетку падает нормально монохроматический свет длиной волны λ = 600 нм. Найти общее число дифракционных максимумов которые дает эта решетка.
Ответ: m_max = 17 .

Задача №7
На узкую щель шириной а = 40 мкм падает под углом θ = 20⁰ к нормали параллельный пучок света с длиной волны λ = 0,6 мкм. В дифракционной картине проектируемой на экран линзой с фокусным расстоянием F = 40 см, ширина центрального максимума Δх . Экран перпендикулярен главной оптической оси линзы, угол θ и угол дифракции φ лежат по одну сторону от нормали. Найти ширину центрального максимума.
Ответ: Δх = 0,27 м.

Задача №8
Можно ли наблюдать дифракционный спектр второго порядка, если ширина щели в два раза больше длины волны? Ответ обосновать.
Ответ: Нет, т.к. второй дифракционный максимум будет наблюдаться под углом дифракции φ = π/2 т.е. на бесконечности .
Задача №9
Можно ли наблюдать дифракционный спектр второго порядка, если период дифракционной решетки в два раза больше длины волны?
Ответ: Нет. Дифракционный спектр второго порядка наблюдать невозможно, т.к. второй и все последующие максимумы кратные отношению d/b = 2, будут исчезать, потому что, под углами соответствующими этим максимумам, щели дифракционной решетки ничего не излучают и каждый максимум кратный отношению d/b = 2 будет исчезать.
Задача №10
Дифракционная решетка содержит 100 штрихов на 1 мм длины решетки. Определить длину волны монохроматического света, падающего на решетку нормально, если угол между двумя спектрами первого порядка равен 8⁰.
Ответ: λ = 1,7 мкм.

Примеры решения задач
Задача №3.2.1
Определить число штрихов на l = 1 см дифракционной решетки, если при нормальном падении света с длиной волны λ = 600 нм решетка дает первый максимум на расстоянии s = 3,3 см от центрального. Расстояние от решетки до экрана L = 110 см.
Д


ано:

l=1 см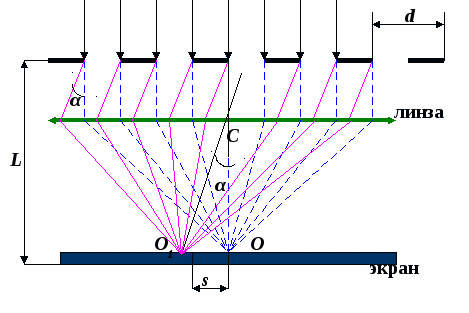

Решение
Число штрихов на 1 см длины решетки определяем по формуле

n_l = 1/d,

где период решетки d найдем из условия максимума для дифракционной решетки :

Условие максимума:

dsinα = kλ

(где α - угол, под которым наблюдается k-й максимум;

k – порядок дифракционного максимума).

Ввиду того, что для максимума 1-го порядка угол α мал, можно принять

sin α ≈ tg α = s/L,

следовательно, условие максимума дифракционной решетки может быть переписано в виде:

ds /L = kλ, откуда можно выразить d:

d = kλL/s ;

таким образом, число штрихов на 1 см длины решетки равен :

n_l = 1/d = s/kλL;

n_l = 500.
Ответ: На 1 см длины решетки 500 штрихов.

Задача №3.2.2
На дифракционную решетку, содержащую n = 500 штрихов на 1 мм, нормально падает белый свет. Спектр проектируется на экран помещенной вблизи решетки линзой. Определить длину спектра первого порядка на экране, если расстояние от линзы до экрана L = 4 м. Границы видимого света: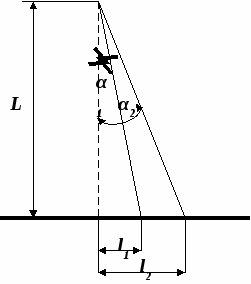

λ_кр = 780 нм, λ_ф = 400нм.

Дано:

nl = 500 l = 1 мм

L = 4м

_λкр = 780 нм

λ_ф = 400 нм

Найти:

∆l =?


Решение
Запишем уравнение дифракционной решетки для случая дифракции красных и фиолетовых лучей:

dsin α₁= kλ_ф;

dsinα₂ = kλ_крα1

Вследствие малости углов α₁ и α₂ в случае спектра первого порядка можно принять:

sin α₁ ≈ tg α₁ = ; sinα₂ ≈ tgα₂ = .

Таким образом,

; ,

и длина спектра

∆l = l₂-l₁ = = knL(λ_кр-λ_ф) = 76 см.
Ответ: ∆l= 76 cм.
Тема № 5 ПОЛЯРИЗАЦИЯ

Задача №1
На какой угловой высоте φ над горизонтом должно находиться Солнце, чтобы солнечный свет, отраженный от поверхности воды, был полностью поляризован ?
Ответ: φ = 37⁰.

Задача №2
Угол Брюстера i_B при падении на кристалл каменной соли равен 57⁰.Определить скорость света в этом кристалле.
Ответ: 194 Мм/с.

Задача №3
Пучок естественного света падает на стеклянный шар, находящийся в воде. Найти угол между отраженным и падающим пучками в точке А (см. рисунок)

.Показатель преломления стекла равен1,58..


Задача №4
Анализатор в k раз (k = 2) уменьшает интенсивность света, приходящего к нему от поляризатора. Определить угол α между направлениями пропускания поляризатора и анализатора. Потерями интенсивности света в анализаторе пренебречь.
Ответ: α = 45⁰.
Задача №5
Во сколько раз ослабляется интенсивность света, проходящего через два николя, направления пропускания которых образуют угол α = 30⁰, если в каждом из николей в отдельности теряется 10% интенсивности падающего на него света?
Ответ: В 3,3 раза.

Задача №6
Угол α между направлениями пропускания поляризатора и анализатора равен 45⁰.Во сколько раз уменьшится интенсивность света , выходящего из анализатора, если угол увеличить до 60⁰?
Ответ: В два раза.

Задача №7
Пучок естественного света падает на стеклянную (n = 1,6) призму, изображенную на рисунке. Определить двугранный угол α призмы, если отраженный луч полностью поляризован.
Ответ: 32⁰.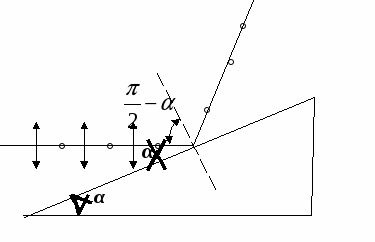



Задача №8
На пути частично-поляризованного света, степень поляризации Р которого равна 0,6 , поставили анализатор так, что интенсивность света , прошедшего через него, стала максимальной. Во сколько раз уменьшится интенсивность света, если направление пропускания анализатора повернуть на угол α = 30⁰?
Ответ: В 1,23 раза.

Задача №9
На поляризатор падает пучок частично поляризованного света. При некотором положении поляризатора, интенсивность света, прошедшего через него, стала минимальной. Когда направление пропускания поляризатора повернули на угол β = 45⁰ , интенсивность света возросла в k раз (k = 1,5).Определить степень поляризации Р света.
Ответ: Р = 0,3.


Задача №10
Лучи естественного света проходят сквозь плоскопараллельную стеклянную пластинку (n = 1,54), падая на нее под углом i_B поляризации. Найти степень поляризации Р лучей , прошедших сквозь пластинку.
Ответ: P = 18,9 %.

Пример решения задач.

Задача 5.1
Найти показатель преломления n стекла, если при отражении от него света отраженный луч будет полностью поляризован при угле преломления β = 35⁰.
Дано

i = φ_B

β = 35⁰

n₁ = 1

Найти:

n₂ = ?

Решение

Запишем закон Брюстера:

tg i_B =

По закону преломления имеем:



Т.к. равны правые части этих уравнений, то можно приравнять и левые части:

tg i_B =

Распишем tgi_B и подставим его значение в последнюю формулу:



В получившемся равенстве у этих двух дробей равны числители, следовательно, равны и знаменатели. В результате имеем:

cos i_B = sin β

Из закона Брюстера имеем:

n₂ = n₁tg i_B = n₁

Заменив выражение sin i_B в последней формуле через cos i_B , получим:

n₂ = n₁tg i_B = n₁

Заменяя выражение для cos i_B ранее выведенным соотношением:

cos i_B = sin β

получим:

n₂ = n_1;

Поставив числовые значения, получим:

n₂ = 1,43.
Ответ: n₂ = 1,43.


Задача №5.2
На пути частично поляризованного света помещен поляроид. При его повороте на угол

α = 60⁰ из положения соответствующего максимальному пропусканию света, интенсивность прошедшего света уменьшается в k = 3 раза. Найти степень поляризации Р падающего света.
Дано:

α = 60⁰

k = 3

Найти:

Р =?

Решение

Интенсивность частично поляризованного света Iч.п. можно представить как совокупность интенсивности линейно поляризованного света Iл.п. и интенсивности I₀ естественного света.

Iч.п. = I0 + Iл.п.

(1)

При произвольном положении поляризатора он пропустит только часть линейно-поляризованного света и половину интенсивности естественного света.

Согласно закону Малюса от интенсивности линейно-поляризованного света поляризатор пропустит только его часть равную Iл.п. = I₀cos²φ /

Следовательно, после поляризатора общая интенсивность пропущенного при этом света I равна:

I =

(2)

где угол φ это угол между направлением пропускания поляризатора и направлением колебания светового вектора в падающем линейно-поляризованном свете.

Следовательно величина I , будет меняться в зависимости от значения cos ²φ :

При этом максимальная интенсивность I_max будет наблюдаться, когд = а cos²φ = 1 (т.е. когда значение cos²φ будет максимальным);

Imax = I1 =

(3)

Соответственно, для минимальной интенсивности света, получим:

Imin = I2 =

(4)

При повороте поляризатора на угол α из положения соответствующего максимальному пропусканию, интенсивность света I₃ становится равной

I3 =

(5)

Согласно условию, интенсивность прошедшего света I₃ уменьшается в k раз по сравнению с максимальной интенсивностью I_max, те.:

(6)

Степень поляризации Р по определению:

P=

(7)

Подставив в формулу (7) выражения для I_max и I_min (формулы (3) и (4) ), получим:

(8)

Из уравнения (6) выразим I₀ и подставим в уравнение (8), получим:
Выразим из уравнения (6) I₀:
kI₀ + kI_л._п.cos²α = I₀ + Iл.п.

I₀(k-1) = Iл.п.(1-kcos²α)

(9)

Полученное выражение для I₀ (формулу (9))

подставим в уравнение (8), получим:
P =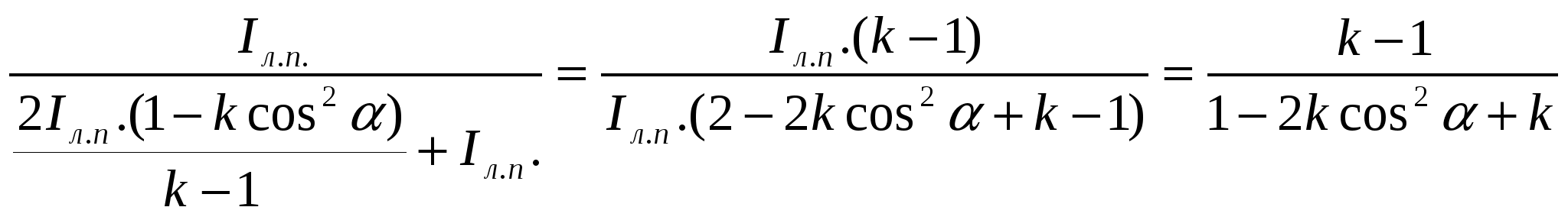

Подставив числовые данные, получим:
Р = 0,8
Ответ: Р = 0,8.

6. Квантовые свойства света
6.1 Тепловое излучение

Задача №6.1.1
Найти температуру Т печи, если известно, что излучение из отверстия в ней площадью

S = 6,1 см² имеет мощность N = 34,6 Вт. Излучение считать близким к излучению абсолютно черного тела.
Ответ: Т = 1000 К.

Задача № 6.1.2
Температура а.ч.т. 127⁰С . После повышения температуры суммарная мощность излучения увеличилась в три раза. На сколько повысилась при этом температура?
Ответ: ∆Т = 126 К

Задача №6.1.3
На сколько изменится длина волны, на которую приходится максимум лучеиспускательной способности при увеличении первоначальной температуры Т₁ равной 1000 К в три раза.
Ответ: ∆λ = 1,926*10^-6 м.

Задача №6.1.4
Абсолютно черное тело имеет температуру Т₁ = 2900 К. В результате остывания тела длина волны, на которую приходится максимум спектральной плотности энергетической светимости, изменилась на ∆λ = 9 мкм. До какой температуры охладилось тело?
Ответ: Т₂ = 290 К.

Задача № 6.1.5
При увеличении термодинамической температуры а.ч.т. в два раза, длина волны на которую приходится максимум лучеиспускательной способности изменилась на 4 мкм.

Определить конечную температуру тела Т₂.
Ответ : Т₂ = 727,5 К

6.2 Внутренний фотоэффект.

Задача №6.2.1

Решение