Операции в базах данных. Тема 2.3 Операции реляционной алгебры. Тема 3 Операции реляционной алгебры
 Скачать 258.39 Kb.
|
|
Тема 2.3 Операции реляционной алгебры. при разработке реляционной модели Эдгар Кодд ввел реляционную алгебру, которая состоит из набора операторов, использующих отношения в качестве операндов и возвращающих отношения в качестве результата. «Начальная алгебра» включает восемь операций: - традиционные операции над множествами: объединение, пересечение, вычитание, декартово произведение; - специальные реляционные операции: выборка, проекция, сединение, деление. Говоря о реляционной алгебре, нельзя обойти вниманием свойство замкнутости. Оно заключается в том, что результат реляционной операции над отношением также является отношением. Следовательно, результат одной операции может использоваться в качестве исходных данных для другой. Таким образом, можно использовать вложенные выражения. Там, где это, возможно, выполняется правило наследования имен атрибутов: соответствующие атрибуты результата будут называться так же, как у исходных отношений. В некоторых случаях также будет выполняться наследование потенциальных ключей. Введем еще одно определение. Два реляционных отношения совместимы по типу если: 1) каждое из них имеет одно и то же множество атрибутов; 2) соответствующие атрибуты (т.е. атрибуты с одинаковыми именами), определены на одном и том же домене. Объединение Объединением двух совместимых по типу отношений А и В называется отношение с тем же заголовком, что у исходных, и с телом, состоящим из множества всех кортежей, принадлежащих А или В, или им обоим. Так как в отношении не может быть двух одинаковых кортежей, операция объединения может сопровождаться удалением дубликатов. Это произойдет в том случае, если полностью совпадающие кортежи встретятся в объединяемых отношениях. А и В: в множестве кортежей, составляющих тело нового отношения, не может быть полностью совпадающих элементов. Степень результата будут равна степени исходных отношений, а кардинальное число - не больше, чем сумма кардинальных числе исходных отношений. Правила записи реляционных операций у разных авторов несколько отличаются. Для записи объединения используют, как правило, одно из двух обозначений: A ᵕ В Aᵕ NION В Первая из этих форм записи аналогична принятой в теории множеств, вторая более близка к форме записи, используемой в языках запросов к БД. Пересечение Пересечением двух совместимых по типу отношений А и В называется отношение с тем же заголовком, что у исходных, и телом, состоящим из множества всех кортежей, принадлежащих обоим отношениям одновременно. Записывается операция так: А ᵔ В A INTERSECT В В Кардинальное число результата пересечения будет не больше, чем наименьшее из кардинальных чисел отношений А и В, степень - равна степеням исходных отношений. Вычитание Вычитанием двух совместимых по типу отношений А и В называется отношение с тем же заголовком, что у исходных, и телом, состоящим из множества всех кортежей, принадлежащих А и не принадлежащих В. Формы записи: А \ В A MINUS В Кардинальное число результата будет не больше кардинального числа А, степень - равна степеням исходных отношений. Поясним введенные определения на примерах. Пусть отношения А и В заданы так, как представлено в табл. 4.2 и 4.3 соответственно. Подчеркиванием обозначено, что атрибут StudID является первичным ключом. Тогда результаты выполнения объединения, пересечения и вычитания отношений А и В представлены в табл. 4.4-4.6 соответственно. Таблица 4.2 Отношение А
Таблица 4.3 Отношение В
Таблица 4.4 Объединение А ᵕ В
Таблица 4.5 Пересечение АᵔВ
Таблица 4.6 Вычитание А/В
Необходимо обратить внимание на следующие моменты. Во-первых, наследование ключей и имен атрибутов позволило определить заголовок результирующего отношения. Во-вторых, встречающийся в обоих отношениях кортеж <123 , Иванов И.И., 382> в результате объединения присутствует в единственном экземпляре, в результате пересечения - является единственным кортежем в теле отношения, в результате вычитания - отсутствует. Так же как при вычитании вещественных чисел, результат А \ В в общем случае не равен результату В \ А. Декартово произведение Декартово произведение двух отношений А и В (где А и В не имеют общих имен атрибутов) определяется как отношение с заголовком, который представляет собой объединение («сцепление») двух заголовков исходных отношений А и В, и телом, состоящим из множества Т всех кортежей, таких, что кортеж t є Т представляет собой сцепление кортежа а є А и кортежа b є В. Кардинальное число результата равно произведению кардинальных чисел исходных отношений, а степень равна сумме их степеней. Запись: А х В A TIMES В Приведем пример декартова произведения. Исходные отношения А и В представлены в табл. 4.7 и 4.8 соответственно. В табл. 4.9 представлен результат декартова произведения. Таблица 4.7 Отношение А
Таблица 4.8 Отношение В
Таблица 4.9 Декартово произведение А х В
Можно убедиться, что степень произведения (табл. 4.9) равна сумме степеней исходных отношений (2+1), а кардинальное число равно произведению кардинальных чисел исходных отношений (3×2) В результирующем отношении получен составной первичный ключ, {StudID Предмет}, тогда как в исходных отношениях он был простым. Стоит обратить внимание на следующие особенности этой операции и операции 0 -соединения, о которой речь пойдет ниже. Если в отношениях А и В оказались одинаковые атрибуты, чтобы различать их в результате, можно условиться формировать имя такого атрибута в виде <имя отношения>. <имя атрибута>. Например, A.FIO и B.FIO. В некоторых случая может понадобиться декартово произведение отношения самого с собой. В этом случае надо использовать еще одну переменную отношения, иначе не удастся правильно сформировать названия атрибутов результата: А1 = A, R = А х А1. Здесь «=» обозначает оператор присваивания. Выборка Выборка - это сокращенное название  -выборки, где  обозначает любой скалярный оператор сравнения (=, >, < и т. д.). 6-выборкой из отношения А по атрибутам X и Y (в этом порядке) называется отношение, имеющее тот же заголовок, что и отношение А, и тело, содержащее множество Т всех кортежей из отношения А, для которых проверка условия «X  Y» дает значение «истина». Формы записи:А [X Y]A WHERE X 0 Y Для операции выборки необходимо, чтобы атрибуты X и Y были определены на одном домене, а оператор должен иметь для него смысл. Константа может быть указана как вместо одного из атрибутов, так и вместо обоих. Рассмотрим пример. В табл. 4.10 представлено отношение STUDENTS, а в табл. 4.11 - результат выборки по условию «Группа = 382».Таблица 4.10 Отношение STUDENTS
Таблица 4.11 Выборка STUDENTS [Группа = 382]
Расширим определение операции -выборки. Будем считать, что условие сравнения для Соединение Определены две разновидности операции соединение: естественное соединение и 0-соединение. Пусть отношения А и В имеют заголовки {X,Y} и {Y,Z}, где атрибуты X,Y,Z могут быть составными. Иными словами, только атрибут Y (или подмножество атрибутов, обозначаемое Y) присутствует как в первом, так и во втором отношении. Атрибуты с одинаковыми именами определены на одних доменах. Тогда естественным соединением отношений А и В называется отношение с заголовком {X,Y,Z,} и телом, содержащим все кортежи {X:x,Y:y,Z:z}, для которых в отношении А значение атрибута X равно х, значение атрибута Y - у, а в отношении В значение атрибута Y равно у, атрибута Z - z. -выборки может содержать произвольное число простых сравнений, соединенных логическими связками. При необходимости, могут использоваться круглые скобки. Для логических связок также используются альтернативные формы записи, одна из которых ближе к принятой в математической логике, другая - к форме записи в языках запросов к БД: - «не» может записываться как —¬ или NOT; - «и» - &, ^ или AND; -«или» - ∨ или OR. Теперь можно построить, например, такое выражение: STUDENTS WHERE ((Группа = 382) AND (StudID < 124)) или используя другой формат записи STUDENTS [Группа = 382 & StudID < 124] Результатом станет отношение, содержащее только кортеж . <123,Иванов И.И., 382>. Проекция Проекцией отношения А по атрибутам V,W,...,Z (где каждый из атрибутов принадлежит отношению А) называется отношение с заголовком {V,W,...Z} и телом, содержащим множество всех кортежей {V:v, W:w,...Z:z}, для которых в отношении А существовал кортеж со значением атрибута V равным v, атрибута W - w, ... и атрибута Z - z. Таким образом, в результате проекции часть атрибутов исходного отношения исключается, после чего может потребоваться удаление повторяющихся кортежей. Проекция отношения А по атрибутам V,W,Z обозначается как А [V, W, Z ] Например, несколько изменим наше отношение STUDENTS (табл. 4.12) и сделаем проекцию по атрибуту «ФИО» (табл. 4.13). Таблица 4.12 Отношение STUDENTS 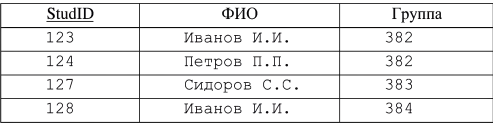 Таблица 4.13 Проекция STUDENTS [ФИО]  Как можно заметить, после отбрасывания атрибутов StudID и «Группа», был получен дублирующийся кортеж <” Иванов И.И.”> который в результате оставлен в одном экземпляре. Подобные ситуации могут возникать, если во множестве атрибутов, на которое делается проекция, не вошел ни один потенциальный ключ исходного отношения. Соединение Определены две разновидности операции соединение: естественное соединение и -соединение. Пусть отношения А и В имеют заголовки {X,Y} и {Y,Z}, где атрибуты X,Y,Z могут быть составными. Иными словами, только атрибут Y (или подмножество атрибутов, обозначаемое Y) присутствует как в первом, так и во втором отношении. Атрибуты с одинаковыми именами определены на одних доменах. Тогда естественным соединением отношений А и В называется отношение с заголовком {X,Y,Z,} и телом, содержащим все кортежи {X:x,Y:y,Z:z}, для которых в отношении А значение атрибута X равно х, значение атрибута Y - у, а в отношении В значение атрибута Y равно у, атрибута Z - z.Обозначается естественное соединение А и В, как A JOIN В. Если отношения А и В не имеют общих имен атрибутов, то их естественное соединение эквивалентно декартовому произведению. В табл. 4.14-4.16 приводится пример естественного соединения двух реляционных отношений. 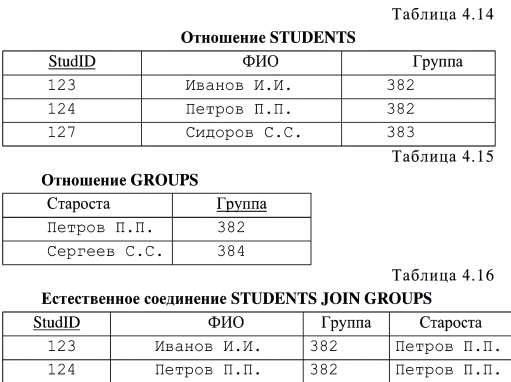 Из-за того, что в первом отношении (табл. 4.14) нет кортежей со значением атрибута «Группа» равным «384», а во втором отношении (табл. 4.15) нет кортежей со значением того же атрибута «383», в результирующем отношении остались только кортежи, содержащие данные о студентах группы «382». Из требований уникальности и неизбыточности для первичного ключа следует, что в результирующем отношении первичный ключ – {StudID} . Пусть отношения А и В не имеют общих атрибутов, и оператор определяется также как в выборке (т. е. оператор сравнения). Тогда в-соединением отношения А по атрибуту X с отношением В по атрибуту Y называется отношение с тем же заголовком, что и при декартовом произведении отношений А и В, и с телом, содержащим множество Т всех кортежей, таких что любой кортеж tєT принадлежит декартовому произведению А и В, и вычисление для него условия «X Y» дает значение «истина». Также как и в случае выборки, X и Y должны быть определены на одном и том же домене, а операция должна иметь смысл для этого домена.На самом деле, -соединение эквивалентно нахождению декартова произведения двух отношений и последующей -выборке, произведенной над результатом. Могут использоваться два варианта записи этой операции: А [X Y] В(A TIMES В) WHERE X Y Рассмотрим пример. Пусть отношение А содержит информацию о цене приборов (табл. 4.17), а отношение В - о цене подставок для приборов (табл. 4.18). Необходимо получить те комбинации приборов, подставок и цен на них, где подставка не дороже прибора. Это можно сделать с помощью операции 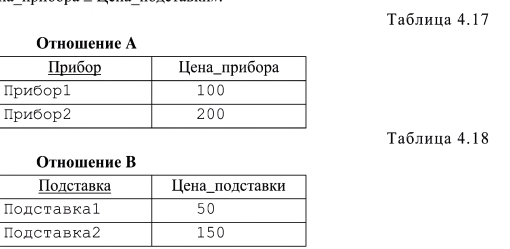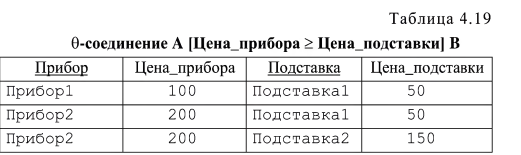-соединения по условию «Цена прибора > Цена подставки».  Деление Пусть отношения А и В имеют заголовки {X, У} и {У} соответственно, атрибуты X и У могут быть составными. Одинаково названные атрибуты двух отношений определены на одних и тех же доменах. Результатом деления отношения А на В будет отношение с заголовком {X} и телом, содержащим множество всех кортежей {Х:х}, таких, что в А существует кортеж {Х:х,У:у}, для всех кортежей {У:у} из В. Обозначается эта операция как: А / В А DIVIDEBY В В табл. 4.20 приведено отношение А, содержащее информацию о том, какой студент сдавал какой предмет. Отношение В содержит список предметов (табл. 4.21). Необходимо получить список идентификаторов студентов, сдавших все перечисленные в таблице В предметы. Задача решается путем деления А на В (табл. 4.22).  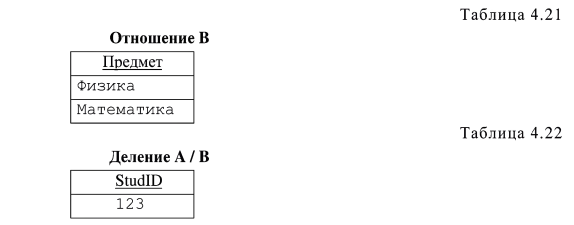 Рассмотрим пример задачи, для решения которой используется несколько реляционных операций. Нужно написать выражение, в результате выполнения которого из отношений STUDENTS (табл. 4.14) и GROUPS (табл. 4.15) будет получено отношение, содержащее данные о фамилии и инициалах студента и старосте его группы. Искомое выражение: (STUDENTS JOIN GROUPS)[ФИО, Староста] Пусть имеется реляционное отношение, которое содержит сле дующие данные о книжных изданиях (табл. 4.23): 1) ID - внутренний идентификатор издания (первичный ключ); 2) Title - название; 3) Author - фамилия и инициалы автора (полагаем, что у одной книги только один автор и среди авторов однофамильцев с совпадающими инициалами нет); 4) Publisher - издательство; 5) Year - год издания. Рассмотрим несколько задач, иллюстрирующих применение операторов реляционной алгебры.  Пусть нужно найти книги, изданные после 1999 года. Причем интересует вся информация о книге. Эта задача решается с помощью выборки. Res = Book[Year>1999] Если требуется перечень всех издательств, о которых имеется упоминание в нашей БД, то будем использовать проекцию. Res = Book[Publisher] Пусть необходимо получить список авторов, издававшихся во всех известных нам издательствах. Просто список издательств был получен в предыдущем примере, аналогично с помощью проекции можно получить список сочетаний «автор»-«издательство», а деление даст искомый результат. Res = (Book[Author,Publisher])/(Book[Publisher]) Чтобы получить список авторов, чьи книги более одного раза издавались в одном и том же году, понадобится -соединение отношения самого с собой. Для этого сначала введем еще одну переменную для отношения Book, потом выполним соединение, проверив, чтобы автор и год совпадали, а издания были различны, и в конце выполним проекцию.В = Book Res = (B[B.ID Ф Book.ID & В.Author = Book.Author & B.Year = Book.Year]Book)[B.Author] Следующая задача - получить список авторов, чьи книги ни разу не издавались в издательстве «Азбука». Часто при решении этой задачи делают ошибку, используя выборку по условию «Publisher» Ф «Азбука». Но это условие, с последующей проекцией, позволит выбрать авторов, которые хотя бы раз издавались в издательстве отличном от «Азбуки», т. е. в общем случае такое решение неверно. Правильное решение будет получено, если из множества всех авторов вычесть тех, кто издавался в «Азбуке». Resl = Book[Author] Res2 = (Book[Publisher = "Азбука"])[Author] Res = Resl \ Res2 |