УМК Физика. Часть 2. Тема 6 Электричество и магнетизм

• Название: Тема 6 Электричество и магнетизм
• Анкор: УМК Физика. Часть 2.docx
• Дата: 17.01.2018
• Размер: 374.52 Kb.
• Имя файла: УМК Физика. Часть 2.docx
• Тип: Документы; #14404
• страница: 2 из 10

Тема № 7 Геометрическая оптика
Оптика изучает свойства и физическую природу света, а также его взаимодействие с веществом. Под светом понимают не только видимый свет, но и примыкающую к нему инфракрасную и ультрафиолетовую области спектра электромагнитных волн.. Оптический спектр охватывает электромагнитные волны с длинами волн условно от 2 мм до 10 нм.

Относительно природы света в науке существовало две точки зрения, -корпускулярная и волновая. В корпускулярной теории, основы которой были заложены Ньютоном, свет представлялся как поток частиц – корпускул, которые двигаются при отсутствии воздействия прямолинейно. В волновой теории, разработанной Гюйгенсом, свет рассматривается как некий волновой процесс, которому присущи такие волновые явления как интерференция и дифракция. Принципиальное различие этих теорий состояло в трактовке относительного показателя преломления . В корпускулярной теории показатель преломления равен отношению скоростей света второй и первой сред, а в волновой теории, наоборот – первой и второй. После того как по методикам Физо и Фуко сравнили скорости света в воздухе и воде и оказалось, что в воздухе она больше, то чаша весов склонилась в сторону волновой теории. После работ Максвелла по электромагнитным волнам мало кто сомневался в правоте волновой теории. Однако в конце ХIХ века были открыты такие явления ,как фотоэффект, объяснить который волновая теория была не в состоянии. В настоящее время считается, что свет представляет некий дуализм волна-частица. В дальнейшем де Бройль высказал предположение, что такой дуализм присущ всем явлениям и объектам микромира и ввёл длину волны для всех частиц. Эта длина волны де Бройля равна

λ_Б = h/mv, (7.1)

где h – постоянная Планка. Мы еще вернёмся позднее к этому вопросу.

Простейшие оптические явления, например получение изображений в оптических приборах, могут быть поняты в рамках так называемой геометрической оптики. В основу формального построения последней положены четыре закона, установленных опытным путём: 1) в однородной среде свет распространяется прямолинейно; 2) световые пучки распространяются в среде независимо от того, присутствуют в ней другие пучки или нет; 3) падающий, отражённый и преломлённый лучи лежат в одной плоскости с нормалью, проведённой к поверхности раздела сред в точке падения луча. Угол отражения равен углу падения , отношение синуса угла падения луча α к синусу угла преломления луча β есть постоянная, называемая относительным показателем преломления n.
sin α/sin β – n (7.2)
Это соотношение называется законом преломления Снеллиуса – Декарта. Относительный показатель преломления равен отношению скоростей света в первой и второй средах. При преломлении света, идущего из оптически более плотной среды, наблюдается явление полного внутреннего отражения, угол полного внутреннего отражения определяется формулой
sin α_вн = 1/n (7.3)
Линзой называется прозрачное тело, ограниченное двумя сферическими или сферической и плоской поверхностями. Линия, проходящая через центры сферических поверхностей, ограничивающих линзу, называется главной оптической осью линзы. После прохождения линзы лучи, идущие до линзы узким пучком параллельно главной оптической оси, или их продолжения пересекаются в точке, которая называется главным фокусом линзы. Если толщина линзы значительно меньше её размеров, линзу называют тонкой. Точку пересечения главной оптической оси с фокусом тонкой линзы называется оптическим центром тонкой линзы. Любой луч, проходящий через оптический центр, называют оптической осью. Расстояние от оптического центра до фокуса называется фокусным расстоянием F линзы. Величина, обратная фокусному расстоянию, называется оптической силой D линзы. Для тонкой линзы оптическая сила определяется выражением

D = (n─1)(1/R₁ ─ 1/R₂) (7.4)
Расстояния отсчитываются от оптического центра, положительным считается направления слева направо. Для тонкой линзы справедлива формула линзы
1/a + 1/b = 1/F, (7.5)
где а – расстояние от предмета до линзы, b – расстояние от линзы до изображения предмета, т.е. точки, в которой после прохождения линзы собираются лучи, исходящие из предмета, или их продолжения. Во втором случае изображение называется мнимым.

При наличии непараксиальных лучей светящаяся точка уже не изображается оптической системой в виде точки. Связанные с этим искажения оптических изображений называется геометрическими аберрациями, Помимо них существуют ещё хроматические аберрации, связанные с дисперсией показателя преломления. Важнейшими геометрическими аберрациями являются : сферическая аберрация; кома; дисторсия; астигматизм косых пучков и искривление плоскости изображения. Для устранения аберраций каждый оптический элемент составляется из нескольких линз, изготовленных из оптических стёкол с различными показателями преломления.

Оптическая система глаза человека состоит из диафрагмы (зрачок – отверстие в радужной оболочке ), хрусталика, стекловидного тела и сетчатки. Радиусы кривизны хрусталика могут изменяться прикреплённой к нему мышцей, при этом изменяется оптическая сила хрусталика, что позволяет человеку рассматривать предметы, расположенные на различных расстояниях. Сетчатка глаза состоит из двух типов приёмников света, палочек и колбочек, палочки более чувствительны и осуществляют видимость при сумеречном освещении, при достаточной освещённости предмета происходит цветное восприятие предметов, т.к. колбочки бывают трёх типов.

Зрение является одним из основных способов познания человеком окружающего мира, поэтому энергию излучения, попадающую на сетчатку глаза человека представляет интерес характеризовать по зрительному или световому ощущению , оцениваемому по действию на глаз человека. Соответствующие характеристики и их единицы называются световыми или фотометрическими, в отличие от энергетических величин и единиц. Основными фотометрическими величинами являются сила света I, световой поток Ф, освещённость Е и др. Силой света источника I в заданном направлении называется световой поток, посылаемый им в этом направлении и отнесённый к единице телесного угла. Световой поток, посылаемый точечным источником в телесный угол dΩ, определяется выражением
dФ = I dΩ,
а полный световой поток, исходящий от источника,
Ф = ∫ I dΩ,
Причём интеграл берётся по полному телесному углу 4π. Единицей силы света СИ является кандела (кд), единицей светового потока является люмен (лм).

Световой поток, приходящийся на единицу площади освещаемой поверхности, называется освещённостью Е этой поверхности. Освещённость поверхности определяется по формуле
Е = I соs θ /r² , (7.6)
где θ – угол между направлением падающих лучей и нормалью к освещаемой поверхности, а

r – расстояние от источника до поверхности. Единицей освещённости является люкс (лк). Освещённость в 75 лк является санитарной нормой для учебных заведений, Солнце даёт освещённость порядка 10⁵лк, полная Луна порядка 0.1 лк.

Простейшая оптическая система состоит из двух линз. Первая, расположенная со стороны предмета (объекта), называется объективом, вторая, расположенная перед глазом человека, называется окуляром. В телескопической системе задний фокус объектива совмещён с передним фокусом окуляра, поэтому параллельный пучок света выходит из системы тоже параллельным, т.е. у системы нет фокуса, поэтому такие системы называют афокальными. Объектив телескопа, - всегда собирающая линза, а окуляром служит либо собирающая, либо рассеивающая линза, в последнем случае изображение получается неперевёрнутым, поэтому такая система используется в биноклях и зрительных труба.

Тема № 8 Волновая оптика.
8.1 Интерференция
В основе явления интерференции лежит нарушение принципа независимости световых пучков

С помощью различных приспособлений можно наложить один световой пучок на другой. Интенсивность света в какой-либо точке пространства, где перекрываются два пучка света, равна I = I₁ + I₂ + I₁₂. Последнее слагаемое I₁₂, учитывающее взаимодействие пучков, называется интерференционным членом, который в некоторых случаях не обращается в нуль. Это явление называется интерференцией волн , а сами пучки когерентны. Рассмотрим интерференцию двух монохроматических пучков света.Интенсивность света пропорциональна квадрату амплитуды, например, вектора напряженности электрического поля. В электромагнитной волне, распространяющейся вдоль оси L, модуль векторов напряженности описываются формулами Е₁ = Е₁₀ соs(ωt─kl₁); Е₂ = Е₂₀ соs(ωt─kl₂), где l₁ и l₂ – расстояния от источников до экрана. По принципу суперпозиции напряженность результирующего поля равна

Е = Е₁ + Е₂, а

Е² = Е₁₀² соs²(ωt─kl₁) + Е₂₀²соs(ωt─kl₂) + 2Е₁₀Е₂₀ соs(ωt─kl₁) соs(ωt─kl₂).,
тогда интерференционный член пропорционален третьему слагаемому в правой части. Так как произведение косинусов равно полусумме косинусов суммы и разности углов, то получаем для этого слагаемого 2Е₁₀Е₂₀ (соs (2ωt ─ k(l₁+l₂)) + соs(k(l₂─l₁))). Первое слагаемое при усреднении даёт нуль, а в случае l₂─l₁ = соnst интерференционный член не равен нудю. Разность l₂─l₁ называется геометрической разностью хода, а её произведение на показатель преломления среды n между источниками и экраном, - оптической разность хода Δ. Разность фаз Δφ равна 2π(l₂─l₁)/λ. Таким образом, лучи когерентны, когда разность фаэ постоянна. \Минимум интерференционной картины соответствует случаю, когда Δφ = (2m+1)π или
Δ = (2m+1)λ/2 , (8.1)
т.е. если оптическая разность хода равна нечётному числу полуволн. Максимум будет наблюдаться , когда 2πm или

Δ = 2m λ/2 , (8.2)
т.е. если оптическая разность хода равна чётному числу полуволн.

Первым интерференцию получил Юнг. Схема опытов Юнга представлена на рис. 1 На закоп-

чёной поверхности стекла I острой

М бритвой прорезана узкая щель S.

S₁ l₁ l₂ Пучок света рассеивается на щели и

S попадает на второе закопчённое

О стекло, на поверхности которого на-

ходятся 2 щели, параллельные S ─

S₂ S₁ и S₂, расстояние между которыми

равно d Если расстояние до экрана

I II L Э равно L, разность хода в точке О Δ=0.

Пусть в точке М наблюдается также

Рис. 8.1 максимум, тогда S₂М ─ S₁М = λ По

теореме Пифагора. Если ОМ = х₁
l₂² = L² + (х₁ + d/2)² l₁² = L² + (х₁ ─d/2)²
Вычитая из первого равенства второе получаем для периода интерференционной картинки в опытах Юнга х₁ формулу
х₁ = l λ/d (8.3)
Рассмотрим использование интерференции для просветления оптики. Для уменьшения коэффициента отражения света от стекла на его поверхность наносится тонкая плёнка, толщина которой подбирается таким образом, чтобы для отраженных от её поверхностей лучей выполнялось условие минимума. Если толщина просветляющего покрытия равна h, а показатель преломления n, то
h = (2m + 1)λ/(4 n) (8.4)
Условие (8.4) выполняется для определенной длины волны, или для двух длин волн, это позволяет в несколько раз уменьшить отражение света от оптических элементов.
8.2 Дифракция .
Под дифракцией света понимают всякое отклонение от прямолинейного распространения света, если оно не может быть истолковано как результат отражения, преломления или изгибания световых лучей в средах непрерывно изменяющимся показателем преломления. Если в среде имеются мельчайшие частицы постороннего вещества, то говорят о рассеянии света и термин «дифракция» не употребляется. Явления дифракции принято классифицировать в зависимости от расстояния источника и точки наблюдения от препятствия. Если эти расстояния очень велики, то дифракция называется дифракцией Фраунгофера, в противоположном случае говорят о дифракции Френеля. Согласно принципу Гюйгенса-Френеля, световое поле источников света в произвольной точке пространства совпадает с результатом интерференции источников вторичных волн, расположенных на поверхности волнового фронта. Френелем разработан приближённый метод разбиения волнового фронта на на кольцевые области, получившие название зон Френеля. Для построения зон Френеля из точки наблюдения проводятся концентрические сферические поверхности, радиусы которых определяются рекурентным соотношением r_i+1 = r_i + λ/2. Излучения чётных и нечётных зон находятся в противофазе. При дифракции Френеля на круглом отверстии результат дифракции зависит от того, какое количество зон Френеля помещается на отверстии, если на нем помещается только первая зона, то в центре картины получается максимум, освещённость в котором в 4 раза превышает освещенность при отсутствии экрана, т.е. такое отверстие работает как собирающая линза.

В случае дифракции Фраунгофера на круглом отверстии радиуса R угловые радиусы тёмных колец определяются формулой
θ_m = (0,61 + (m – 1)/2)λ/R. , (8.5)
Если под R понимать радиус зрачка глаза человека, то по формуле (8.5) можно оценить минимальное расстояние, которое может разрешить человеческий глаз. Это расстояние приблизительно равняется половине длины волны.

Важнейший элемент современных спектральных приборов – дифракционная решётка. Она представляет собой плоскую стеклянную или металлическую поверхность, на которой делительной машиной нарезано очень много (N до 10⁵) прямых равноотстоящих штрихов. В случае нормального падения лучей угловые направления на дифракционные максимумы определяются известной формулой
d sin θ_m = m λ, (8.6)
где d – период решётки. Для спектральных приборов важной характеристикой расстояния между длинами волн соседних спектральных линий Δλ, которые разрешает прибор. Величина
R = λ/Δλ (8.7)
называется разрешающей способностью прибора. Для дифракционной решётки
R = m N (8.8)
Разрешающая способность дифракционной решётки на несколько порядков превышает разрешающую способность использованных ранее стеклянных призм.
8.3 Специальная теория относительности
Теория относительности ─ фундаментальная физическая теория, охватывающая всю физику. Она была создана А. Эйнштейном в начале ХХ века. В её основе лежат постулаты, твёрдо установленные экспериментально.Теория относительности применительно к инерциальным системам отсчёта называется специальной теорией относительности. В её основе лежат два постулата. Первый, называемый принципом относительности, утверждает, что законы природы, определяющие изменение состояний физических систем, не зависят от того, к какой из двух инерциальных систем отсчёта, движущихся одна относительно другой прямолинейно и равномерно, они относятся. Во втором постулате говорится о независимости скорости света в вакууме от скорости движения источника света.

Рассмотрим основные релятивистские эффекты:

1.Длина движущегося стержня короче, чем покоящегося. Это явление называется лоренцевым сокращением длины.

l = l₀ 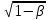² , (8.9)

где β = v/с, - отношение скорости тела к скорости света в вакууме.

2. Замедление хода движущихся часов
Δt₀ = Δt 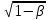² (8.10_)
3. Закон сложения скоростей для двух тел, двигающихся со скоростями v₁ и v₂ навстречу друг другу определяется по формуле
v₁₂ = (v₁ + v₂)/(1 + v₁v₂/с²) (8.11)
4. Масса движущегося тела увеличивается
m = m₀/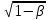² (8.12)
5. Полная энергия тела равна

Е = m с² (8.13)
6. Для фотона и других безмассовых частиц связь между энергией и импульсом имеет вид
Р = Е/с (8.14)
Основные формулы специальной теории относительности прошли всестороннюю экспериментальную проверку. Релятивистское замедление времени было подтверждено в явлении распада мюонов. Так называются нестабильные заряженные частицы , масса которых в 207 раз больше массы электрона, которые образуются в верхних слоях атмосферы на высоте порядка 10 км. Расчёты времени жизни быстрых мюонов дали значение приблизительно τ=10^-5 с. Космические мюоны замедлялись в свинцовом блоке и с помощью специального устройства отфильтровывались медленные мюоны. Измерения показали, что время жизни медленного мюона τ₀ = 2.2 10^-6 с, что в пределах погрешности измерений совпадает с результатами расчёта по формуле (8.10).
Тема № 9 Физика атома
9.1 Световые кванты.
Гипотеза о квантах возникла в процессе установления закономерностей теплового излучения и была высказана Планком в 1900 г. Гипотеза Планка состоит в том, что излучение и поглощение света происходит не непрерывно, а конечными порциями, называемыми квантами света или квантами энергии. Впоследствии эта гипотеза развилась в стройное и глубокое учение, покорившее всю физику.

Излучение света происходит в результате переходов атомов, молекул и других атомных систем из состояний с большей энергией в состояние с меньшей энергией. Так называемое тепловое или температурное излучение отличается от других видов излучения (люминесценции) только способом перехода излучающих систем в возбуждённое состояние. Закон Кирхгофа для теплового излучения утверждает, что отношение излучательной способности тела к его поглощательной способности является универсальной функцией частоты и температуры. Тело называется абсолютно чёрным, если его поглощательная способность равна единице. В 1879 г. Стефан установил экспериментально, что для чёрных тел интегральная плотность излучения пропорциональна четвёртой степени абсолютной температуры. Через пять лет Больцман получил этот результат теоретически. Закон Стефана-Больцмана имеет вид

Е_ачт = σ Т⁴ , (9.1)
где σ = 5.67 10^-8 Вт/(м² К⁴) – постоянная Стефана-Больцмана.

Распределение спектральной плотности излучения абсолютно чёрного тела по длинам волн было тщательно изучено экспериментально. Максимум кривых λ_m при повышении температуры смещается в сторону более коротких длин волн. Вильгельм Вин в 1894 г. доказал, что

λ_m Т = b = const . (9.2)
Этот результат называется законом смещения Вина. Постоянная Вина b = 2,90 10_-3 м·К.

Однако вывести уравнение кривой зависимости спектральной плотности излучения абсолютно чёрного тела от частоты ν классическая термодинамика оказалась не в состоянии. Эта формула была получена Планком с помощью уже упомянутой гипотезы
Е_ачт = 4hν³/(с³(exp(hν/kT) ─ 1) , (9.3)
где h = 6.63 10^-34 Дж с - постоянная Планка.
Идея Планка о квантах была применена Эйнштейном для объяснения фотоэффекта, открытого Герцем в 1887 г. и тщательно исследованного Столетовым, который экспериментально установил три закона для фотоэффекта:

1) максимальная начальная скорость фотоэлектронов определяется частотой света и не зависит от его интенсивности;

2) для каждого вещества существует красная граница фотоэффекта, т.е. наименьшая частота, при которой ещё возможен фотоэффект;

3) число фотоэлектронов, вырываемых из катода за 1 с, прямо пропорционально интенсивности света.

Эти законы были объяснены Эйнштейном, предположившим, что электромагнитная волна состоит из отдельных порций – квантов, названных впоследствии фотонами. Уравнение Эйнштейна для фотоэффекта имеет вид
hν = A₀ + mv²/2 ? (9/4)
где А₀ – работа выхода электронов из металла
9.2 Модель атома Резерфорда-Бора.
В конце ХIХ века в физике и химии накопилось достаточное количество результатов, из которых можно было сделать вывод о существовании внутри атомов электрических зарядов. При исследовании катодных лучей Дж. Дж. Томсон открыл электрон, он же предложи первую модель строения вещества, состоящую из заряженных частей. В 1911 г. Резерфорд на основании известных опытов по рассеянию α-частиц на тонкой металлической фольге установил, что атом состоит из положительно заряженного ядра и окружающей его электронной оболочки. Линейные размеры ядра порядка 10^-15 м, а размеры самого атома в 10⁵ раз больше, однако 99,95 % массы атома сосредоточено в его ядре. Резерфорд предложил планетарную модель строения атома. Однако, согласно классической электродинамике, электрический заряд, движущийся ускоренно, излучает электромагнитные волны. Теряя энергию на излучение, электрон непрерывно приближался бы к ядру и в конце концов упал бы на него. Таким образом классическая электродинамика оказалась не в состоянии объяснить существование атомов как устойчивых систем атомных ядер и электронов. Решение этой проблемы было получено только в рамках квантовой механики. Это ясно понял Нильс Бор, сформулировавший в 1913 г. два постулата: 1) Атом может находиться только в некоторых избранных (квантовых) состояниях, характеризующихся дискретными значениями энергии E₁, E₂, E₃,…..В этих состояниях, вопреки классической электродинамике, атом не излучает; 2) При переходе из стационарного состояния с большей энергией Е₂ в стационарное состояние с меньшей энергией Е₁ , если такое изменение происходит из-за излучения, атом излучает фотон с энергией h ν = Е₂ – Е₁.

2

Модель атома Резерфорда-Бора хорошо объяснила спектр излучения атома водорода, в частности смысл целых чисел, входящих в эмпирическую формулу Ридберга
ν_nm = R_Н (1/n² – 1/m² ). (9.5)
где m > n.

Правило квантования стационарных орбит первоначально заключалось в том, что на длине орбиты должно укладываться целое число длин волн де Бройля
2πr = n h/mv (9.6)
По второму закона Ньютона

mv²_/r = Се²/r², (9.7)
где С – коэффициент пропорциональности в законе Кулона. Из этих формул легко получить, что энергия электрона равна
Е = m С²е⁴4π²/(2h³n²) (9.8)
Таким образом энергия атома обратно пропорциональна квадрату целого числа n, называемого главным квантовым числом. Из формулы (9.5) получаются все известные спектральные серии Лаймана (n = 1), Бальмера (n = 2), Пашена (n = 3) и т. д. Однако все попытки объяснить спектры излучения более сложных атомов закончились неудачей. Это связано с непоследовательностью теории Бора. Существование стационарных состояний атома совершенно непонятно с точки зрения классической физики. В то же время к движению электронов в стационарных состояниях теория Бора применяла законы классической механики, хотя и считала неприменимой классическую электродинамику. Теория Бора в целом является только промежуточным этапом на пути к более совершенной и последовательной теории – квантовой механики.

В 1916 году Эйнштейн при рассмотрении механизма излучения света ввёл понятие индуцированного излучения. Если атом самопроизвольно переходит из высшего энергетического состояния в низшее с испусканием света, то такое излучение называется спонтанным. Однако, если атом находится в световом поле, то оно может вынуждать переход с высшего уровня на низший, излучение в этом случае называется индуцированным (вынужденным). На этом явлении основан принцип работы лазера. Если на атом падает фотон с энергией h ν = Е₂ – Е₁, где Е₁ и Е₂ – какие-либо два энергетических уровня этого атома, то падающий фотон, если атом находится на высшем уровне Е₂, может вызвать переход атома на низший уровень Е₁ с испусканием второго фотона который характеризуется не только той же частотой ν , но также теми же фазой, поляризацией и направлением распространения. Если атомов много, то в обычном состоянии на каждом простом верхнем уровне находится меньше атомов, чем на нижнем. Можно искусственно получить среду с инверсной заселённостью энергетических уровней (активную среду). Эта идея усиления света в активной среде за счёт индуцированного излучения была реализована в середине 20 века.