свимя. Тема Числовые последовательности Тема Предел последовательности Тема Понятие функции Тема Элементарные функции Тема Пределы функций Общее количество вопросов 20 (из 70)
 Скачать 377.86 Kb. Скачать 377.86 Kb.
|
|
Рубежный контроль 1 модуля 2 Темы 3.1-3.5. Раздел 3. «Введение в математический анализ» Тема 3.1. Числовые последовательности Тема 3.2. Предел последовательности Тема 3.3. Понятие функции Тема 3.4. Элементарные функции Тема 3.5. Пределы функций Общее количество вопросов – 20 (из 70). Время прохождения теста – 120 минут. Максимальное количество баллов за тест – 100. Заголовки секций НЕ показывать.
Критерии оценивания
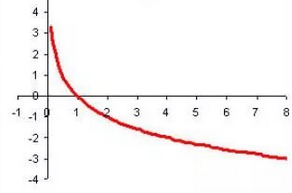
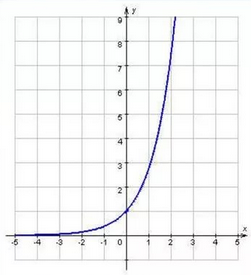
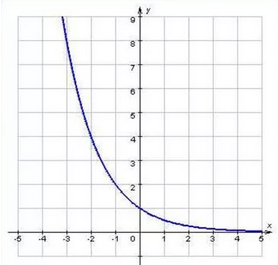
Секция 1. Тема 3.1. Числовые последовательности. Тема 3.2. Предел последовательности (??) Укажите верные утверждения относительно последовательности 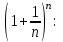 (!) последовательность ограничена (?) последовательность убывает с ростом n (?) последовательность неограниченная (?) последовательность фундаментальная (??) Если формула n-го члена числовой последовательности имеет вид 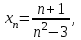 то x5 равно (!) 3/11 (?) 3/14 (?) 1/5 (?) 5/13 (??) Какие из последовательностей являются ограниченными: 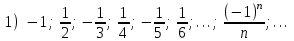 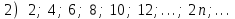 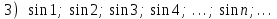 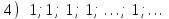 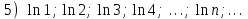 (!) 1; 3; 4 (?) все (?) 1; 3 (?) 1; 3; 4; 5 (??) Найти предел последовательности: 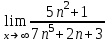 (!) 0 (?) 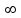 (?) -5 (?) 7 (??) Найти предел последовательности 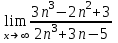 . .(!) 3/2 (?) 2/3 (?) 0 (?) -3/5 (??) Найти предел последовательности 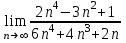 . .(!) 1/3 (?) ∞ (?) 0 (?) 1/2 (??) Вычислите 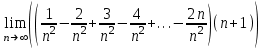 (!) -1 (?) 0 (?) 1 (?) не существует (??) Вычислите 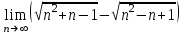 (!) 1 (?) 0 (?)∞ (?) 2 Секция 2. Тема 3.3. Понятие функции. Тема 3.4. Элементарные функции (??) Величина y в выражении y=f(x) является: (!) зависимой переменной (?) независимой переменной (?) аппликатой (?) аргументом (??) Величина 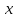 в выражении y=f(x) является: в выражении y=f(x) является:(!) независимой переменной (?) зависимой переменной (?) аппликатой (?) функцией (??) Сложной функцией называется: (!) функция, аргументом которой является другая функция (?) функция, представляющая собой сумму или разность нескольких функций (?) если она является логарифмом х (?) функция, представляющая собой произведение нескольких функций (??) График функции y=xsinx представляет собой (!) произведение графиков двух функций: y=x и y=sinx (?) сумму графиков двух функций: y=x и y=sinx (?) разность графиков двух функций: y=x и y=sinx (?) произведение графиков двух функций: y=1 и y=sinx (??) Какая из приведенных функций является степенной? (!) 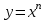 (?) 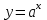 (?) 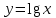 (?) 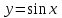 (??) Функция 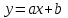 является: является:(!) линейной (?) показательной (?) логарифмической (?) тригонометрической (??) Какое из следующих утверждений верно? (!) функции, не являющиеся ни четными, ни нечетными, называют функциями общего вида (?) функция у = f(x) называется нечетной, если для xX f(x) = f(-x) (?) функция называется непериодической, если существует число Т0 такое, что для xX: 1) x+ТX; 2) f(x+Т) = f(x), где число Т называется периодом функции (?) функция у = f(x) называется четной, если для xX f(x) = -f(-x) (??) Какой график соответствует показательной функции с положительным основанием, меньшим 1?
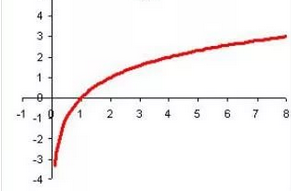
(!) в) (?) а) (?) б) (?) г) (??) Какой график соответствует логарифмической функции с положительным основанием, меньшим 1?
(!) г) (?) а) (?) б) (?) в) (??) Чему равен период функции 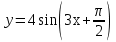 ? ?(!) 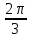 (?) 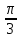 (?) 0 (?) 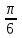 (??) Чему равен период функции 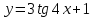 ? ?(!) 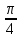 (?) 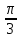 (?) 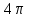 (?) 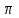 (??) Чему равен период функции 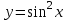 ? ?(!) 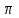 (?) 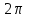 (?) 0 (?) 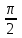 (??) Укажите область значений функции 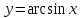 . .(!) 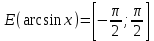 (?) 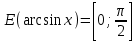 (?) 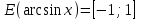 (?) 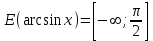 (??) Какие из функций четные? 1) 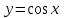 ; 2) ; 2) 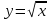 ; 3) ; 3) 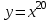 ; 4) ; 4) 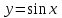 . .(!) 1) и 3) (?) 2) и 4) (?) 1) и 2) (?) 2) и 3) (??) Дана функция 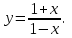 Найти 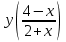 (!) 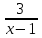 (?) -2 (?) 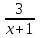 (?) 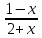 (??) Дана функция 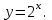 Найти 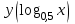 (!) 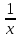 (?) x (?) 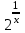 (?) 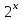 (??) Найти область определения функции 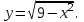 (!) 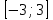 (?) 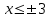 (?) 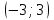 (?) 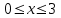 (??) Найти область определения функции 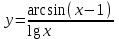 (!) 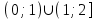 (?) 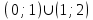 (?) 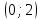 (?) 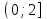 (??) Найти область определения функции 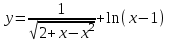 (!) 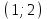 (?) 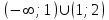 (?) 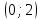 (?) 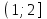 (??) Найти обратную функцию для функции 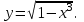 (!) 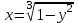 (?) 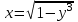 (?) 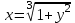 (?) 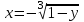 Секция 3. Тема 3.5. Пределы функций. Теория. (??) Какое выражение означает левый предел функции в точке: (!) 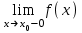 (?) 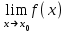 (?) 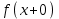 (?) 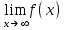 (??) Первый замечательный предел это: (!) 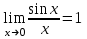 (?) 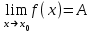 (?) 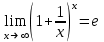 (?) 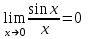 (??) Если функция имеет конечные левый и правый предел в точке x0, и они равны значению функции в этой точке, то в точке x0 (!) функция непрерывна (?) функция дифференцируема (?) имеет разрыв 1 рода (?) имеет разрыв 2 рода (??) Функция непрерывна в точке x0, если (!) 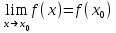 (?) 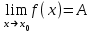 (?) 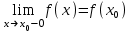 (?) 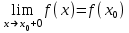 (??) Определить точки разрыва функции 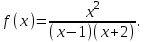 (!) 1 и -2 (?) -1 и 2 (?) 0 и 1 (?) -1 и -2 (??) Для того чтобы существовал предел функции в конечной точке a необходимо и достаточно, чтобы (!) существовали и были равны односторонние пределы в точке a (?) существовали и были неравны односторонние пределы в точке a (?) односторонние пределы в точке a не существовали (?)односторонние пределы в точке a были равны нулю (??) Если функция имеет бесконечный односторонний предел в точке x0, то (!) имеет разрыв 2 рода (?) функция непрерывна (?) имеет разрыв 1 рода (?) точек разрыва нет (??) Второй замечательный предел это: (!) 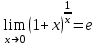 (?) 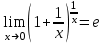 (?) 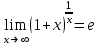 (?) 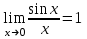 (??) Если функция имеет конечные левый и правый предел в точке x0, но они не равны, то (!) имеет разрыв 1 рода (?) функция непрерывна (?) имеет разрыв 2 рода (?) функция дифференцируема (??) Какое выражение означает правый предел в точке: (!) 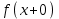 (?) 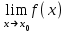 (?) 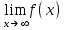 (?) 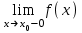 (??) Если 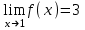 и f(x) - четная функция, то 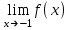 равен (!) 3 (?) 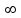 (?) 0 (?) не существует (??) Эквивалентность двух бесконечно малых величин обозначается знаком (!) (?) 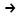 (?) 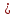 (?) 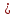 (??) Дано 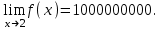 . .Укажите верное утверждение. (!) f(x) ограничена в окрестности точки x=2 (?)f(x) - бесконечно большая при x→2 (?) 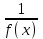 - - бесконечно большая при x→2 (?) 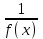 - - бесконечно малая при x→2 (??) Известно, что при x→0 α(x), β(x) - бесконечно малые и 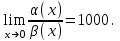 Какое из следующих утверждений верно при x→0? (!)α(x) и β(x) одного порядка малости (?) α(x) и β(x) эквивалентны (?)α(x) более высокого порядка малости, чем β(x) (?)α(x) более низкого порядка малости, чем β(x) (??) Известно, что при x→x0 бесконечно малые α(x), β(x) эквивалентны. Какое из следующих утверждений верно при x→x0? (!)α(x) и β(x) одного порядка малости (?)α(x) более высокого порядка малости, чем β(x) (?)α(x) более низкого порядка малости, чем β(x) (?)α(x) и β(x) нельзя сравнивать (??) При x→1 укажите верное утверждение (!) 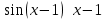 (?) 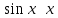 (?) 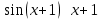 (?) 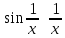 (??) Известно, что 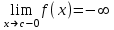 , , 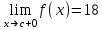 . .Какое из утверждений верно? (!)Точка c – точка разрыва второго рода (?) Точка c – точка неустранимого разрыва первого рода (?)Точка c – точка устранимого разрыва первого рода (?)Точка c – точка непрерывности (??) Известно, что 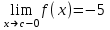 , , 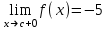 , , 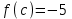 . .Какое из утверждений верно? (!)Точка c – точка непрерывности (?)Точка c – точка неустранимого разрыва первого рода (?)Точка c – точка устранимого разрыва первого рода (?)Точка c – точка разрыва второго рода (??) Укажите, в каком случае в точке с функция f(x) имеет устранимый разрыв: (!) 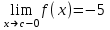 , , 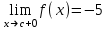 , , 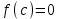 (?) 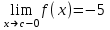 , , 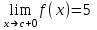 , , 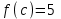 (?) 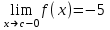 , , 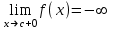 (?) 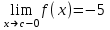 , , 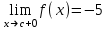 , , 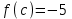 (??) Известно, что f(x) – непрерывная функция. Какое из следующих утверждений верно? (!) 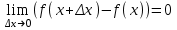 (?) 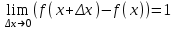 (?) 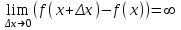 (?) 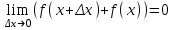 (??) Функция f(x) имеет устранимый разрыв в точке x=2 и 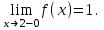 Тогда 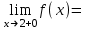 (!) 1 (?) 0 (?) -1 (?) 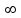 (??) Укажите функцию непрерывную в точке x=1: (!) 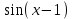 (?) 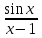 (?) 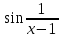 (?) 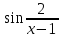 Секция 4. Тема 3.5. Пределы функций. Вычисление пределов. Часть 1. (??) Вычислите: 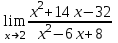 (!) -9 (?) -32 (?) 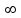 (?) 0 (??) Вычислите: 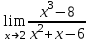 (!) 2,4 (?) 4 (?) 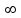 (?) 0 (??) Вычислите: 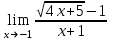 (!) 2 (?) -2 (?) -1 (?) 0 (??) Вычислите: 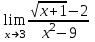 (!) 1/24 (?) 1/6 (?) 1/4 (?) 0 (??) Если 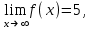 то 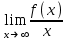 равен (!) 0 (?) 3 (?) 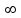 (?) не существует (??) Если 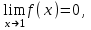 то 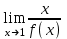 равен (!) 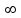 (?) 1 (?) 0 (?) не существует (??) Если 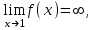 то 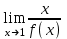 равен (!) 0 (?) -1 (?) 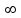 (?) не существует (??) Найти односторонние пределы при x→2 слева и справа для функции 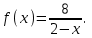 (!) 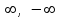 , , (?) 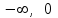 (?)  (?) 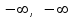 (??) Вычислить 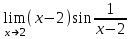 (!) 0 (?) 1 (?) 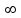 (?) не существует (??) Вычислить 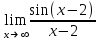 (!) 0 (?) -1 (?) 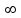 (?) не существует (??) Вычислить 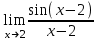 (!) 1 (?) -1 (?) 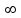 (?) не существует (??) Вычислите 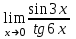 (!) 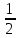 (?) 3 (?) 6 (?) 0 Секция 5. Тема 3.5. Пределы функций. Вычисление пределов. Часть 2. (??) Вычислите 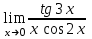 (!) 3 (?) 1 (?) 3/2 (?) 0 (??) Если 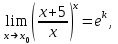 то k равно (!) 5 (?) 1 (?) 0 (?) 0,2 (??) Заменяя эквивалентными бесконечно малыми, найдите предел 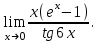 (!) 0 (?) 2 (?) не существует (?) 1/6 (??) Заменяя эквивалентными бесконечно малыми, найдите предел 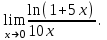 (!) 0,5 (?) 1 (?) не существует (?) 1 (??) Заменяя эквивалентными бесконечно малыми, найдите предел 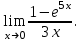 (!) -5/3 (?) 5/3 (?) не существует (?) 0 (??) Заменяя эквивалентными бесконечно малыми, найдите предел 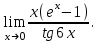 (!) 0 (?) 2 (?) не существует (?) 1/6 (??) Заменяя эквивалентными бесконечно малыми, найдите предел 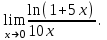 (!) 0,5 (?) 1 (?) не существует (?) 1 (??) Заменяя эквивалентными бесконечно малыми, найдите предел 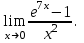 (!) ∞ (?) 7 (?) 1 (?) 0 |