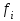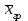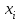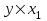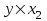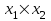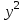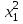Тема Экономикостатистический анализ наличия и эффективности использования основных фондов на примере конкретного предприятия (региона)
 Скачать 1.6 Mb. Скачать 1.6 Mb.
|
|
Определяем число групп с равными интервалами: 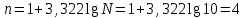 Определяем величину интервала по формуле: 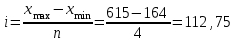 Группировка регионов СФО по уровню ВРП на душу населения в 2020 г. представлена в таблице 5. Таблица 5 – Группировка регионов СФО по ВРП на душу населения в 2020 г.
1 группа: 164+112,75=276,75 2 группа: 276,75+112,75=389,5 3 группа: 389,5+112,75=502,25 4 группа: 502,25+112,75=615 Самой многочисленной группой в группировке регионов Сибирского федерального округа по ВРП на душу населения является первая в интервале от 164 до 277, в нее входит 50% регионов (5 из 10). ВРП на душу населения в первой группе составил 206 тыс. руб./чел., что на 34,39% ниже чем среднерегиональный уровень (206/314*100-100=-34,39%). В группу с ВРП на душу населения от 502 до 615 попал только один регион (615 тыс. руб./чел.). Из группировки видно, что с ростом ВРП на душу населения увеличивается коэффициент занятости, т.е. наблюдается прямая связь. Для более глубокого изучения связи между анализируемыми признаками построим комбинационную группировку (табл. 6). Таблица 6 – Комбинационная группировка регионов СФО по уровню среднего душевого дохода и ВРП на душу населения в 2020 г.
Данные комбинационной группировки свидетельствуют о прямой связи между уровнем занятости населения и уровнем среднего душевого дохода, а также между уровнем занятости населения и ВРП на душу населения. 2.2 Дисперсионный анализ Для характеристики тесноты связей между признаками в аналитической группировке (табл. 6) рассчитаем эмпирическое корреляционное отношение и коэффициент детерминации. Для этого необходимо определить общую, межгрупповую и внутригрупповую дисперсии. Общая дисперсия отражает вариацию в целом и вычисляется по формуле: 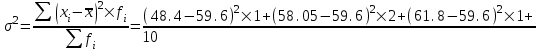 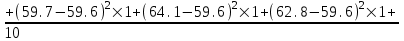 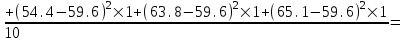 24,0515 24,0515Дисперсия групповых связей (межгрупповая дисперсия) показывает вариацию признака за счет того фактора, который положен в основу группировки: 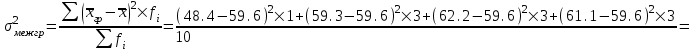 =15,274 =15,274Внутригрупповая дисперсия рассчитывается по формуле: 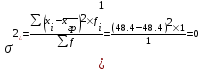 ; ;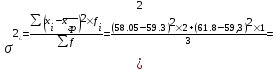 3,125; 3,125;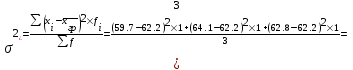 =3,406667 =3,406667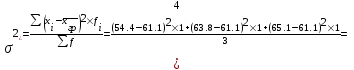 =22,72667 =22,72667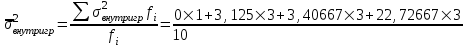 =8,7775 Средняя из внутригрупповых дисперсий характеризует вариацию, возникающую под влиянием случайных факторов, кроме групповых: Общая дисперсия равна сумме межгрупповой и средней из внутригрупповых дисперсий. Это равенство называется правилом сложения дисперсий: 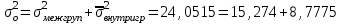 . .Эмпирическое корреляционное отношение характеризует тесноту корреляционной зависимости: 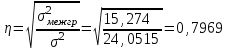 . .Коэффициент детерминации характеризует долю вариации результативного признака, вызванную действием факторного признака, положенного в основу группировки: 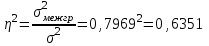 . .Таким образом, общая дисперсия составляет 24,0515%, из которой вариация за счет факторов, положенных в основу группировки (уровень среднего душевого дохода и ВРП на душу населения) обусловлена на 63,51%, а 36,49% (100-63,51=36,49) обусловлено другими факторами. 2.3 Корреляционно-регрессионный анализ факторов, влияющих на уровень занятости населения В этом разделе выполним корреляционно-регрессионный анализ факторов, влияющих на уровень занятости населения (уровня среднего душевого дохода и ВРП на душу населения). Для этого построим вспомогательную таблицу 7. Таблица 7 – Вспомогательная таблица для проведения корреляционно-регрессионного анализа
Рассчитаем парные коэффициенты корреляции. Парный коэффициент корреляции между уровнем занятости и уровнем среднего душевого дохода: 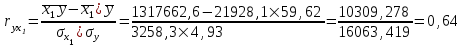 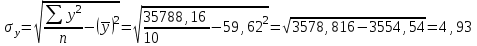 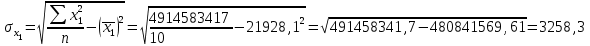 . .Связь между уровнем занятости и уровнем среднего душевого дохода проявилась прямая (если положительная, то прямая, отрицательная - обратная) заметная (определяется по шкале). Для справки: Атрибутивная оценка тесноты корреляционной зависимости: До 0,3 – слабая (практически отсутствует); 0,3 – 0,5 – умеренная; 0,5 – 0,7 – связь заметная; 0,7 – 0,9 – связь тесная;  0,9 – связь весьма тесная. 0,9 – связь весьма тесная.Парный коэффициент корреляции уровнем занятости и ВРП на душу населения: 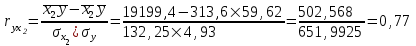 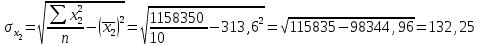 . .Связь между уровнем занятости и ВРП на душу населения проявилась прямая тесная. Парный коэффициент корреляции между уровнем среднего душевого дохода и ВРП на душу населения: 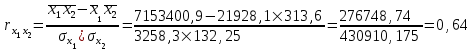 Связь между уровнем среднего душевого дохода и ВРП на душу населения проявилась прямая заметная. Множественной коэффициент корреляции найдем по формуле: 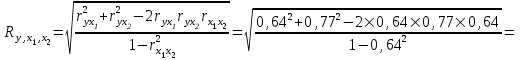 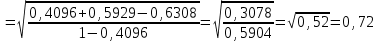 . .Коэффициент детерминации по множественному коэффициенту корреляции составляет: 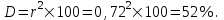 Он показывает, что уровень занятости населения Сибирского федерального округа на 52% зависит от изменения уровня среднего душевого дохода и ВРП на душу населения. Средняя квадратическая ошибка множественного коэффициента корреляции составляет: 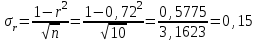 . .Далее построим уравнение множественной регрессии, которое имеет следующий вид: 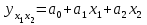 . .Параметры уравнения определим из системы нормальных уравнений: 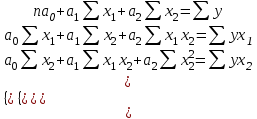 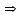 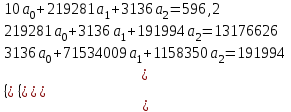    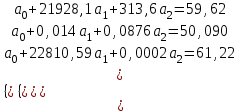 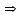 вычитаем из первого уравнения второе, из второго третье: 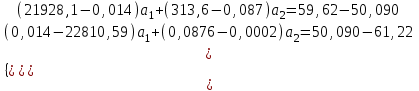 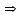 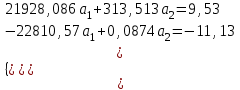 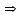 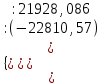 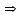 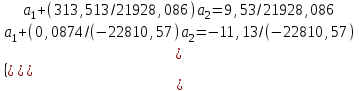 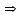 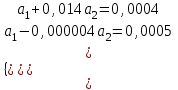 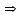 Вычитаем из первого уравнения второе:  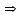  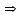   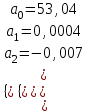  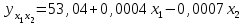 Уравнение регрессии показывает, что с изменением уровня среднего душевого дохода на 1 руб./мес. коэффициент занятости изменится на 0,0004%, с изменением ВРП на душу населения на 1 руб./чел. уменьшается на 0,0007%. Для более глубокого анализа рассчитаем частные коэффициенты эластичности: 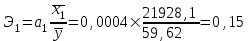 ; ; 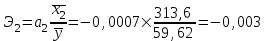 , ,где 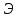 – коэффициент эластичности, – коэффициент эластичности, 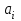 – коэффициент регрессии при соответствующем факторном признаке, – коэффициент регрессии при соответствующем факторном признаке, 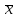 – среднее значение факторного признака, – среднее значение факторного признака, 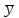 – среднее значение результативного признака. – среднее значение результативного признака.Коэффициенты эластичности свидетельствуют о том, что с изменением уровня среднего душевого дохода на 1% уровень занятости изменится на 0,15%, с изменением ВРП на душу населения на 1% уровень занятости изменится на 0,12%. Компьютерная обработка цифровой информации (если есть желание, то можно выполнить все расчеты по разделу 2.3 с помощью пакета прикладных программ Microsoft Office Excel)  Обработку данных можно выполнить, воспользовавшись ПК и пакетами прикладных программ Excel, EViews, Statgraphics, Statistika и т.д. В данном учебном пособии рассмотрим способы и приемы обработки цифровой информации с помощью пакета Microsoft Office Excel 2010. |