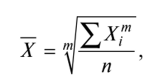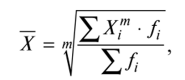Апап. Статистика платная. На какие группы делятся средние величины
 Скачать 1.47 Mb. Скачать 1.47 Mb.
|
|
Блок 1 На какие группы делятся средние величины?
Формулы расчета степенных средних включают показатель степени (т). В зависимости от его значения различается: • средняя гармоническая, если т = -1; • средняя геометрическая, если т = 0; • средняя арифметическая, если т= 1; • средняя квадратическая, если т = 2; • средняя кубическая, если т = 3 и т.д. Если рассчитать все виды средних для одних и тех же исходных данных, то их значения окажутся неодинаковыми. Здесь действует правило мажорантности: с возрастанием показателя степени т увеличивается и соответствующая средняя величина: При каких условиях используются средние степенные простые величины? Средние величины используются на этапе обработки и обобщения полученных первичных статистических данных. Потребность определения средних величин связана с тем, что у различных единиц исследуемых совокупностей индивидуальные значения одного и того же признака, как правило, неодинаковы. При каких условиях требуется использование средних степенных взвешенных величин? Ответ: Если данные представлены первичным признаком (потому что показатели, выраженные превичным признаком, могут быть непосредственно измерены сосчитаны), если данные с группированы в вариационных рядах распределения. В чем отличие и сходство средней арифметической взвешенной и средней гармонической взвешенной? Средняя арифметическая взвешенная, используется, когда в задаче есть знаменатель(fi), а средняя гармоническая взвешенная используется, когда есть числитель. Обе формулы используются при наличие у показателя вторичного признака Что такое дисперсия? В чем измеряется? Дисперсия- средняя величина из квадратов отклонений значений признака от средней величины. Дисперсия считается безмерной величиной.  Из за трудности интерпретации дисперсии переходят от дисперсии к среднему квадратическому отклонению:  Среднее квадратическое отклонениеизмеряется в единицах исходной информации В чем различие в использовании простой и взвешенной формулы для расчета дисперсии? Степенные средние могут быть простыми и взвешенными. Простая средняя величина рассчитывается при наличии двух и более несгруппированных статистических величин, расположенных в произвольном порядке по следующей общей формуле: 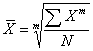 Взвешенная средняя величина рассчитывается по сгруппированным статистическим величинам с использованием следующей общей формулы: 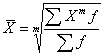 Что такое среднее квадратическое отклонение? В чем его преимущество перед дисперсией? Среднеквадратическим отклонением называют значение квадратного корня из дисперсии случайной величины D. Среднее квадратическое отклонение показывает, на сколько в среднем отклоняются конкретные значения признака от среднего их значения. Преимущество среднего квадратического отклонения перед дисперсией состоит в том, что оно является именованной величиной, т.е. имеет ту же единицу измерения, что и значения признака. Что такое коэффициент вариации? В чем измеряется? Для чего используется? В теории вероятности и статистике, коэффициент вариации, также известный как относительное стандартное отклонение, это стандартная мера дисперсии распределения вероятностей или частотного распределения. Она часто выражается в процентах и определяется как отношение стандартного отклонения σ к среднему μ. КВ или СОО широко используются в аналитической химии для выражения точности и повторяемости анализа. Они также часто применяются в инженерии и физике, при проведении исследований по обеспечению качества. Кроме того, КВ используется экономистами и инвесторами в экономических моделях. Что такое ряд динамики? Из каких элементов состоит? Ряд динамики (хронологический, динамический, временной) – это последовательность упорядоченных во времени числовых показателей, характеризующих уровень развития изучаемого явления. Ряд динамики состоит из двух элементов: 1) периодов или моментов времени (t); 2) уровней изучаемого показателя (у). Какие типы рядов динамики бывают? По времени — ряды моментные и интервальные (периодные), которые показывают уровень явления на конкретный момент времени или на определенный его период. Сумма уровней интервального ряда дает вполне реальную статистическую величину за несколько периодов времени, например, общий выпуск продукции, общее количество проданных акций и т.п. Уровни моментного ряда, хотя и можно суммировать, но эта сумма реального содержания, как правило, не имеет. Так, если сложить величины запасов на начало каждого месяца квартала, то полученная сумма не означает квартальную величину запасов. По форме представления — ряды абсолютных, относительных и средних величин. По интервалам времени — ряды равномерные и неравномерные (полные и неполные), первые из которых имеют равные интервалы, а у вторых равенство интервалов не соблюдается. По числу смысловых статистических величин — ряды изолированные и комплексные (одномерные и многомерные). Первые представляют собой ряд динамики одной статистической величины (например, индекс инфляции), а вторые — нескольких (например, потребление основных продуктов питания). Что такой абсолютный прирост? Чем отличаются цепные и базисные абсолютные приросты? Абсолютный прирост – характеризует изменение показателя за один или несколько последовательных периодов времени в абсолютном выражении; Измеряется в тех же единицах, что и исходная информация Может быть как положительная, так и отрицательная Абсолютный прирост называется цепным если за базу сравнения принят уровень предыдущего периода Базисный прирост называется базисным если за базу сравнения принят какой либо определенный уровень, (чаще начальный)  Что такое темп роста? Чем отличается от коэффициента роста? Темп роста (Тр) — это показатель интенсивности изменения уровня ряда, который выражается в процентах, определяет общую динамику показателя за один или несколько последовательных периодов времени, а в долях выражается коэффициент роста (Кр). Коэффициент роста определяется как отношение последующего уровня к предыдущему или к показателю принятому за базу сравнения. Он определяет, во сколько раз увеличился уровень по сравнению с базисным, а в случае уменьшения- какую часть базисного уровня составляет сравниваемый. Темп роста всегда положительный. Расчеты темпа роста: цепной, базисный Как проявляется взаимосвязь между цепными и базисными темпами роста? Между базисными и цепными темпами роста, выраженными в форме коэффициентов, имеется определенная взаимосвязь, которая заключается в следующем: • во-первых, произведение последовательных цепных темпов роста равно базисному темпу роста за соответствующий период; • во-вторых, частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста. Указанные зависимости между темпами роста можно использовать для преобразования базисных темпов в цепные и наоборот, особенно в тех случаях, когда неизвестны абсолютные уровни динамики. Что такое темп прироста? Как рассчитывается? Темп прироста – относительная величина прироста, то есть отношение абсолютного прироста к предыдущему или базисному уровню. Характеризует, на сколько процентов уровень данного периода больше (или меньше) базисного уровня. 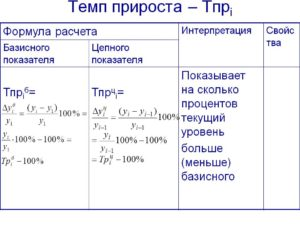 В чем отличие в интерпретации темпов роста и темпов прироста? Темп роста – относительный экономический показатель, показывающий процентный рост одного показателя над аналогичным показателем прошлого периода. Темп прироста – самый универсальный сравнительный показатель эффективности, он показывает, НА СКОЛЬКО процентов вырос или снизился один показатель по сравнению с аналогичным показателем более раннего периода. Почему для первого уровня ряда во временном ряду цепные показатели (абсолютный прирост, темп роста, темп прироста) невозможно рассчитать? Потому что цепной показатель рассчитывается в пределах исследуемого промежутка, т.к. это первый уровень, то это начало промежутка, цепной показатель не рассчитать из-за отсутствия уровня перед ним. Чему равен базисный абсолютный прирост для первого года (даты) во временном ряду? Базисный абсолютный прирост – разность между сравниваемым уровнем ряда Равен 0,0 Чему равен базисный темп роста для первого года (даты) во временном ряду? Темп роста базисный – отношением каждого последующего уровня к одному и тому же уровню, принятому за базу сравнения. В данном случае равен 100%. От чего зависит расчет среднего уровня ряда? Каждый ряд динамики можно рассматривать как некую совокупность n меняющихся во времени показателей, которые можно обобщать в виде средних величин. Такие обобщенные (средние) показатели особенно необходимы при сравнении изменений того или иного показателя в разные периоды, в разных странах и т.д. Обобщенной характеристикой ряда динамики может служить прежде всего средний уровень ряда. Способ расчета среднего уровня зависит от того, моментный ряд или интервальный (периодный). В случае интервального ряда его средний уровень определяется по формуле простой средней арифметической величины из уровней ряда. Если имеется моментный ряд, содержащий n уровней (y1, y2, …, yn) с равными промежутками между датами (моментами времени), то такой ряд легко преобразовать в ряд средних величин. При этом показатель (уровень) на начало каждого периода одновременно является показателем на конец предыдущего периода. Тогда средняя величина показателя для каждого периода (промежутка между датами) может быть рассчитана как полусумма значений у на начало и конец периода По какой формуле рассчитывается средний уровень интервального ряда с равными (неравными) интервалами?  По какой формуле рассчитывается средний уровень моментного ряда с равными интервалами между датами? Почему нельзя использовать среднюю арифметическую простую? средний уровень моментного ряда с равными интервалами между датами рассчитывается по средней хронологической простой. Средняя арифметическая простая используется при работе с не сгруппированными данными. Как рассчитывается средний абсолютный прирост? Вычисляется путем деления общего прироста за весь период на длину этого периода в тех или иных единицах времени: Δ Δ По какой формуле рассчитывает средний темп роста? Название средней величины!  Yt- текущий уровень показателя Yt-1 предыдущий уровень показателя Kpt -коэффициент роста Y0 -базисный уровень показателя Крt-коэффициент текущего уровня Трn -Темп роста базисный Является интервальным показателем, т.е. характеризуют тот или иной промежуток времени Определяет общую динамику показателя за один или несколько последовательных периодов времени; Измеряется в процентах (доля единицы – коэффициент роста); Может принимать только положительные значения ( значение сравнивают с100%) От чего зависит выбор формулы (простой или взвешенной) для расчета среднего темпа роста? Средний темп роста служит сводной обобщающей характеристикой интенсивности изменения уровней ряда динамики. Он показывает, сколько в среднем процентов последующий уровень составляет от предыдущего в течение всего периода наблюдения Средняя арифметическая простая (невзвешенная) – вычисляется когда каждый вариант совокупности встречается только один раз. Средняя арифметическая (взвешенная) – варианты повторяются различное число раз, при этом число повторений вариантов называется частотой, или статистическим весом. Средняя арифметическая простая – самый распространенный вид средней величины, рассчитывается по формуле . 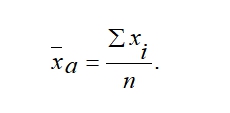 Средняя арифметическая взвешенная формула . 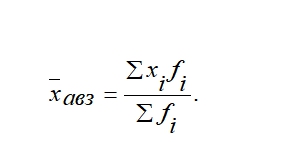 Что показывает абсолютное значение 1% прироста? Абсолютное значение 1% прироста (А%) — это отношение абсолютного прироста к темпу прироста, выраженный в процентах и показывает значимость каждого процента прироста за тот же период времени. (Абсолютное значение 1% прироста показывает, сколько единиц надо произвести в данном периоде, чтобы уровень предыдущего периода возрос на 1 %.) Что такое индекс? Индекс — число, буквы или другая комбинация символов, указывающая место элемента в совокупности или характеризующая состояние некоторой системы, например показатель активности, производительности, развития, изменения чего-либо. Индексация в экономике — это средство защиты от инфляции путём привязки суммы договора, кредита, зарплаты, пенсии, пособий, вкладов и т. п. к индексу потребительских цен. Что такое индивидуальный индекс? На какой статистический показатель он похож? Индивидуальные индексы характеризуют соотношение отдельных элементов совокупности. Похож на темп роста Как рассчитывают индивидуальные индексы цен и физического объема? Индивидуальный индекс цен Индивидуальный индекс физического объема Индивидуальный индекс обозначается буквой Что такое общий (сводный) индекс? Когда применяется? Какие бывают? Индекс- показатель сравнения двух состояний одного и того же явления. Сводный (общий) индекс представляет собой относительный показатель, отражающий изменение группы однородных элементов изучаемого экономического явления Непосредственно несоизмеримых из-за качественных различий. Бывают Агрегатные и средневзвешенные из индивидуальных Позволяют сопоставлять сложные явления-совокупности объектов (товаров например) По составляющим агрегатные индексы похожи на средние взвешенные величины, а именно: - Индексируемая величина (величина, динамика которой изучается) - признак-вес, позволяющих обобщить разнородные элементы совокупности.    Pi- цена за единицу продукции 0-базисный (предыдущий) период, 1- отчетный период Qi количество продукции  Pi- цена за единицу продукции 0-базисный (предыдущий) период, 1- отчетный период Qi -количество продукции  Pi- цена за единицу прдукции 0-базисный (предыдущий) период, 1- отчетный период Qi количество продукции Ipq – сводный индекс оборота товаров IpL – индекс цен по Ласпейресу Iqp -индекс физического объема Пааше Что такое агрегатные индексы? В какой системе они связываются? Агрегатными называются индексы, которые строятся непосредственно по данным об индексируемых величинах и весах. В качестве показателей-весов (соизмерителей) может использоваться показатель либо базисного, либо отчетного периода. Непосредственно цены на разные товары суммировать нельзя, поэтому для получения суммы каждую цену нужно взвешивать на натуральные объемы потребления (продаж и пр.)товаров. Формула индексов используется используют показатели двух периодов:0-базисный(предыдущий); 1-отчетный(текущий) Формула Ласпейреса (веса –показатели базисного периода) Пааше (веса-показатели отчетного периода) Связываются в системе мультипликативных индексов. Чем отличаются агрегатные индексы цен по Ласпейресу и по Пааше? Индекс Паше преобразуется в средний гармонический индекс цен, а индекс Ласпейреса — в средний арифметический индекс цен. Индекс Пааше численно должен быть меньше индекса Ласпейреса. Разница в результатах расчета по этим формулам называется эффектом Геншенкрона. Чем отличаются агрегатные индексы физического объема по Ласпейресу и по Пааше? Для характеристики среднего изменения цен на потребительские товары используют индекс цен, предложенный Ласпейресом. Если количество набора продуктов принимается на уровне отчетного периода, то в этом случае индекс цен именуется индексом Пааше. Как рассчитывается сводный индекс стоимости оборота товаров и услуг? Какой факторный анализ можно с его помощью провести? Ipg=Ip  Ig IgIpg – сводный индекс; Ip – индекс цен; Ig – индекс объема 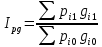 - прямая формула индекса оборота товаров и услуг. (берем один товар умножаем его цену на его объем плюс следующие товары так же «цена*объем» все это складываем получаем числитель. Знаменатель по такому же принципу. Потом делим). - прямая формула индекса оборота товаров и услуг. (берем один товар умножаем его цену на его объем плюс следующие товары так же «цена*объем» все это складываем получаем числитель. Знаменатель по такому же принципу. Потом делим). С его помощью можно сопоставить сложные явления совокупности объектов. Что такое средневзвешенные индексы из индивидуальных? Когда они используются? Средневзвешенный индекс - средняя величина из индивидуальных индексов. При его расчете используются две формы средних величин: арифметическая и гармоническая. Применение той или иной формулы средневзвешенного индекса зависит от имеющейся в распоряжении информации. К их исчислению прибегают тогда, когда имеющаяся в распоряжении информация не позволяет рассчитать общий агрегатный индекс. Так, если отсутствуют данные о ценах, но имеется информация о стоимости продукции в текущем периоде и известны индивидуальные индексы цен по каждому товару, то нельзя определить общий индекс цент как агрегатный, но возможно исчислить общий индекс физического объема продукции как средневзвешенную величину. Каких видов бывают средневзвешенные индексы?   P- цена за единицу прдукции 0-базисный (предыдущий) период, 1- отчетный период Q количество продукции i-индивидуальный индекс  P- цена за единицу прдукции 0-базисный (предыдущий) период, 1- отчетный период Q количество продукции i-индивидуальный индекс P- цена за единицу прдукции 0-базисный (предыдущий) период, 1- отчетный период Q количество продукции i-индивидуальный индекс 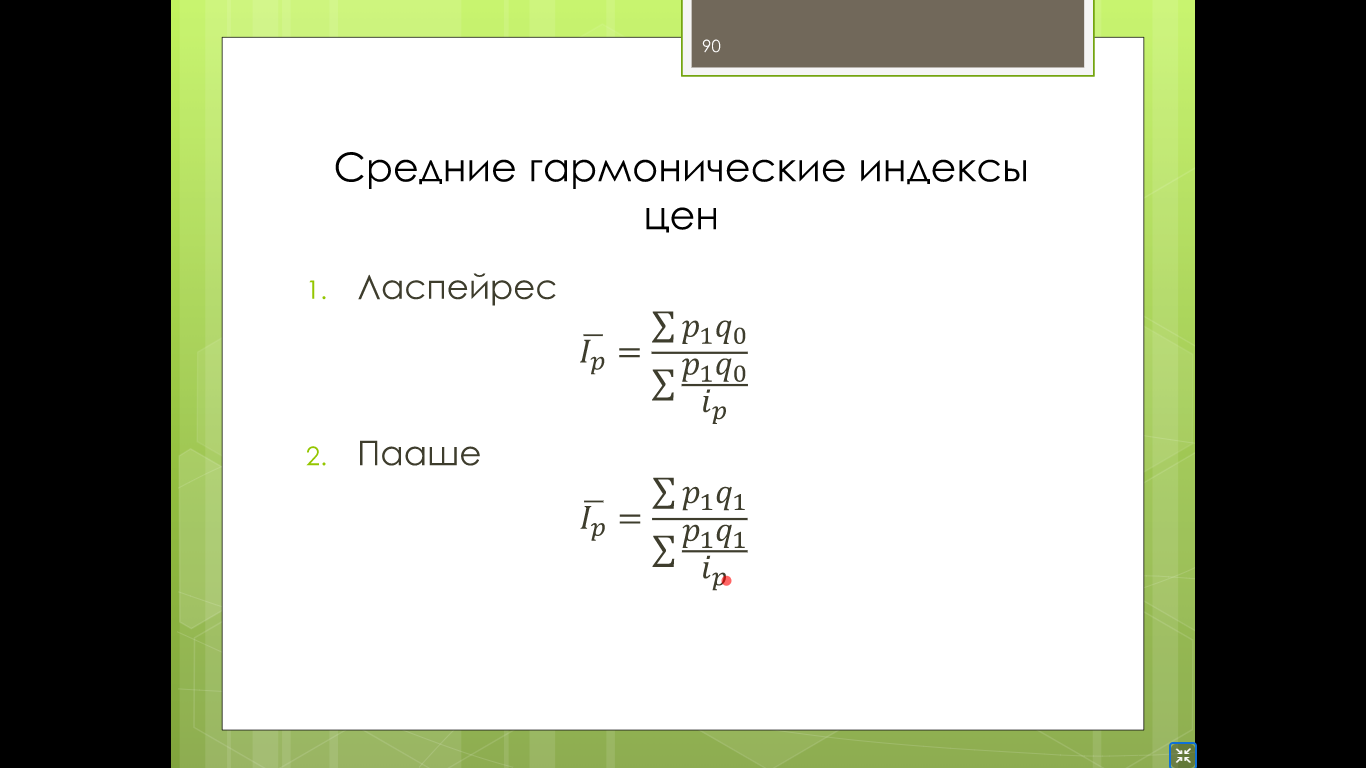 Блок 2 Если нужно рассчитать среднюю величину показателя «число больничных коек на 10000 человек», известно число больничных коек на 10000 человек в каждом регионе и общее число больничных коек в каждом регионе, какую формулу выберете? (название формулы) Ответ: выберем формулу средней гармонической взвешенной, так как известен числитель логической формулы. Если нужно рассчитать среднюю величину показателя «число больничных коек на 10000 человек», известно число больничных коек на 10000 человек в каждом регионе и численность населения регионов, какую формулу выберете? (название формулы) Ответ: выберем формулу средней арифметической взвешенной, так как известен знаменатель логической формулы. Известны доли численности детей в общей численности населения (в %) по городам и общая численность населения по городам, по какой формуле будет рассчитана средняя доля численности детей? Ответ: средняя доля численности детей будет рассчитана по формуле средней арифметической взвешенной, так как известен знаменатель логической формулы. Имеются данные о налогах на продукты в млрд. руб. по регионам, в чем будет измеряться среднее значение налогов на продукты и дисперсия? Ответ: среднее значение налогов на продукты будет измеряться в млрд. руб., дисперсия единицы измерения не имеет. Имеются данные о численности рабочей силы в тыс. чел. по регионам, в чем будет измеряться среднее значение численности рабочей силы и среднее квадратическое отклонение? Ответ: среднее значение численности рабочей силы и среднее квадратическое отклонение будут измеряться в тыс. чел. Если коэффициент вариации равен 15%, что можно сказать о средней величине? Ответ: средняя величина является типичной и достоверной характеристикой для исследуемой совокупности. Если коэффициент вариации равен 56%, что можно сказать о средней величине? Ответ: средняя величина является нетипичной и недостоверной характеристикой для исследуемой совокупности Если средняя величина равна 10 рублям, а среднее квадратическое отклонение – 3 рублям, какой будет формулировка вывода по этим показателям? Ответ: в среднем конкретные значения признака отклоняются от их среднего значения (10 рублей) на 3 рубля в ту или иную сторону, наиболее характерные значения признака находятся в пределах от 7 до 13 руб. (диапазон 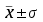 ). ).Представлен временной ряд, составленный по показателю «наличие основных фондов на конец года, млрд. руб.», с 2015 по 2019 гг. Что будет написано в итоговой строке по этому показателю? Ответ: будет написан «–» (прочерк) или знак Х, так как показатели моментных рядов не обладают свойством суммирования. Представлен временной ряд, составленный по показателю «объем прямых иностранных инвестиций, млн. руб.», с 2015 по 2019 гг. Что будет написано в итоговой строке по этому показателю? Ответ: сумма показателей ряда динамики (так как ряд интервальный). Чем по временным характеристикам отличаются показатели «численность населения на 1 января» и «валовая добавленная стоимость»? Ответ: «численность населения на 1 января» – развитие явления на определенную дату (моментный ряд динамики); валовая добавленная стоимость» – развитие явления за определенный интервал времени – месяц, квартал, год (интервальный ряд динамики). Сумма приростов численности населения в тыс. чел. к предыдущему году (за 2014, 2015, 2016, 2017 годы) равна 30,5 тыс. чел. Чему равен прирост численности населения в тыс. чел. к 2013 году? Ответ: 30,5 тыс. чел. Сумма цепных абсолютных приростов за период равна базисному приросту последнего периода ряда динамики за этот же период. Временной ряд включает в себя 7 уровней, сколько цепных абсолютных приростов можно посчитать? Ответ: 6. Временной ряд включает в себя 8 уровней, сколько базисных абсолютных приростов можно посчитать? Ответ: 8, если считать абсолютный прирост базисного года, равный нулю. Временной ряд включает в себя 5 уровней, сколько темпов роста, % к предыдущему году можно рассчитать для данного временного ряда? Ответ: 4. Временной ряд включает в себя 10 уровней (с 2010 г. по 2019 г.), сколько темпов роста, % к 2010 г. можно рассчитать? Ответ: 10, если считать базисный темп роста 2010 года, равный 100%. Временной ряд включает в себя 7 уровней, сколько темпов прироста, % к предыдущему году можно рассчитать для данного временного ряда? Ответ: 6. Имеется показатель «численность населения на 1 января, тыс. чел», в чем будет измеряться абсолютное значение 1% прироста? Ответ: в тыс. чел. Темп роста численности населения в 2018 г. составил 102,3%, какой можно сделать вывод? Ответ: численность населения в 2018 г. увеличилась на 2,3%. Число больничных коек в 2019 г. выросло на 5,4%, чему равен темп роста числа больничных коек в 2019 г.? Ответ: 105,4%. Темп роста численности рабочей силы составил 98,8%, какой вывод можно сделать? Ответ: численность рабочей силы снизилась на 1,2%. Численность занятых уменьшилась на 5,4%, чем равен темп роста численности занятых? Ответ: 94,6%. Имеются данные о ценах на 5 товаров, сколько индивидуальных индексов цен и физического объема можно рассчитать? Ответ: 10 индексов всего: 5 индивидуальных индексов цен и 5 индивидуальных индексов физического объема. Имеются данные о ценах на 5 товаров, сколько общих индексов цен и физического объема можно рассчитать? Ответ: 2 общий индекса: 1 общий индекс цен и 1 общий индекс физического объема. Если в сентябре общий индекс цен в регионе составил 103,4%, какой вывод можно сделать об изменении цен? Ответ: в сентябре цены в среднем в регионе выросли на 3,4%. Если средний уровень цен на товары и услуги в июне по сравнению с маем снизился на 3,7%, то чему равен общий индекс цен? Ответ: 0,963 (96,3%) Если дисперсия равна 1000, что можно сказать о изучаемой совокупности? Ответ: дисперсия – это средний квадрат отклонений значений признака от их средней величины. Дисперсия еще не дает представления об однородности совокупности, этому показателю трудно дать экономическую интерпретацию, так как он рассчитан в квадратных единицах. Для того, чтобы судить об изучаемой совокупности, нужно рассчитать среднее квадратическое отклонение: 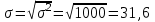 В изучаемой совокупности в среднем конкретные значения признака отклоняются от их среднего значения на 31,6 в ту или иную сторону. Рассчитана средняя цена на яблоки, и она измеряется в рублях, в чем будет измеряться коэффициент вариации? Ответ: в процентах. Если общий индекс физического объема равен 98,7%, что можно сказать о динамике количества производимых товаров? Ответ: количество производимых товаров в среднем снизилось на 1,3%. Если общий индекс цен составил 102,5%, а индивидуальный 99,8%, если ли в этом противоречие? Какой вывод можно сделать? Ответ: нет противоречия. Индивидуальные индексы характеризуют изменение отдельных единиц статистической совокупности, а общий индекс характеризует изменение по всей совокупности элементов сложного явления. Цена отдельного товара могла снизиться на 0,2% (индивидуальный индекс 99,8%), а другого – увеличиться. Общий индекс цен, равный 102,5% показывает, что в среднем цены на несколько товаров выросли на 2,5%, несмотря на то, что цена одного товара снизилась на 0,2%. БЛОК 3 На предприятии работают 15 работников с заработной платой 25700 руб., 5 работников с заработной платой 23400 руб., 2 работника с заработной платой 23950 руб. и 2 работника с заработной платой 24 тыс. руб. Чему равна средняя заработная плата на данном предприятии? Решение: 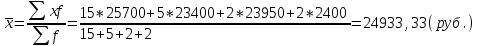 Известно, что общий выпуск продукции на 1 предприятии составил 100 тыс. руб., на втором – 150 тыс. руб., цена продукции 1 предприятия равна 100 рублей, 2 предприятия – 105 рублей. Чему равна средняя цена по двум предприятиям? Решение: 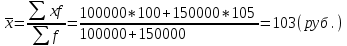 В интервале от 10 до 20 тыс. руб. находилась заработная плата 15 работников, в интервале от 20 до 40 тыс. руб. – 20 работников, в интервале от 40 до 60 тыс. руб. – 5 работников. Чему равна средняя заработная плата всех работников? Решение: Найдем средину интервалов 1)(10+20)/2=15тыс.руб. 2)(20+40)/2=30тыс.руб. 3) (40+60)/2=50тыс.руб. Средняя заработная плата всех работников составит 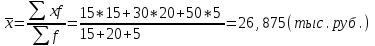 Если темп роста равен 110% за 4 года, чему равен средний темп роста в этот период? Решение: Средний темп роста равен 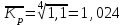 Временной ряд состоит из 5 уровней, уровень первого периода = 100 млн. руб., уровень последнего периода = 120 млн. руб., чему равен средний темп роста? Решение: Средний темп роста равен 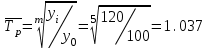 Временной ряд состоит из 5 уровней, уровень первого периода = 100 млн. руб., уровень последнего периода = 120 млн. руб., чему равен базисный абсолютный прирост последнего периода и среднегодовой абсолютный прирост? Решение: Базисный абсолютный прирост равен: 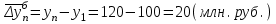 Среднегодовой абсолютный прирост равен 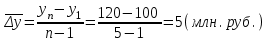 На 1 января товарные запасы оценивались в 300 тыс. руб., на 1 февраля – 320 тыс. руб., на 1 марта – 325 тыс. руб., на 1 апреля – 280 тыс. руб. Чему равен средний уровень товарных запасов в 1 квартале года? Решение: Средний уровень товарных запасов в 1 квартале будет определятся по формуле средней арифметической взвешенной, так как промежутки между датами не равные: 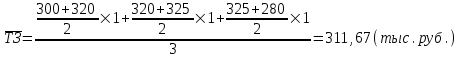 На 1 января численность населения города была 105,9 тыс. чел., на 1 марта – 105,7 тыс. чел., на 1 августа – 106,1 тыс. чел., на 1 января следующего года – 106,4 тыс. чел. Чему равна среднегодовая численность населения города? Решение: 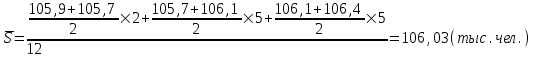 Коэффициенты роста к предыдущему году составили: в 2014 г. – 1,004 в 2015 г. -1,021, в 2016 г. – 1,033, в 2017 г. – 1,089. Чему равен базисный темп роста в 2017 г. (к 2013 г.)? Решение: Коэффициент роста рассчитывается 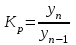 Темп роста рассчитывается: 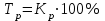 Следовательно: 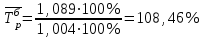 Коэффициенты роста к предыдущему году составили: в 2014 г. – 1,004 в 2015 г. -1,021, в 2016 г. – 1,033, в 2017 г. – 1,089. Чему равен средний темп роста в 2014-2017 гг.? Решение: Средний темп роста равен 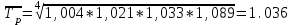 Оборот розничной торговли в мае составил 150 тыс. руб., в июне – 200 тыс. руб. Чему равен сводный индекс оборота товаров? Решение: Сводный индекс оборота товаров: 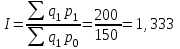 Цена товара А в январе составила 100 рублей, в феврале – 104 рубля. Цена товара Б в январе – 98 руб., в феврале – 102 руб. В январе было продано товара А – 20 шт., товара Б – 15 шт., в феврале – 23 и 17 шт. соответственно. Чему равен общий индекс цен? Решение: 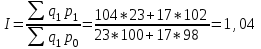 В среднем цены увеличились на 4% Цена товара А в январе составила 100 рублей, в феврале – 104 рубля. Цена товара Б в январе – 98 руб., в феврале – 102 руб. В январе было продано товара А – 20 шт., товара Б – 15 шт., в феврале – 23 и 17 шт. соответственно. Чему равен общий индекс физического объема? Решение: 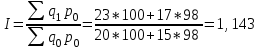 В среднем физический объем увеличились на 14,3% Цена товара А в январе составила 100 рублей, в феврале – 104 рубля. Цена товара Б в январе – 98 руб., в феврале – 102 руб. В январе было продано товара А – 20 шт., товара Б – 15 шт., в феврале – 23 и 17 шт. соответственно. Чему равен общий индекс оборота товаров? Решение: 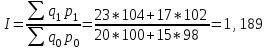 В среднем товарооборот увеличились на 18,9% Цена товара А в январе составила 100 рублей, в феврале – 104 рубля. Цена товара Б в январе – 98 руб., в феврале – 102 руб. В январе было продано товара А – 20 шт., товара Б – 15 шт., в феврале – 23 и 17 шт. соответственно. Рассчитайте индивидуальные индексы цен? Решение: Для товара А 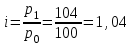 Для товара Б 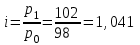 Цена товара А в январе составила 100 рублей, в феврале – 104 рубля. Цена товара Б в январе – 98 руб., в феврале – 102 руб. В январе было продано товара А – 20 шт., товара Б – 15 шт., в феврале – 23 и 17 шт. соответственно. Рассчитайте индивидуальные индексы физического объема. Решение: Для товара А 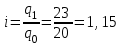 Для товара Б 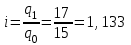 Оборот товаров в базисном периоде составил 100 тыс. руб., затем тот же натуральный объем (физический объем товаров в базисном периоде) оценили в ценах отчетного периода – 135,4 тыс. руб. Как изменились цены на все товары в среднем в отчетном периоде по сравнению с базисным? Решение: 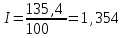 Выросли на 35,4% Выросли на 35,4%Если цены в отчетном периоде выросли на 3,4%, а индекс физического объема составил 98,3%. Чему равен индекс стоимости оборота товаров и услуг? Решение: 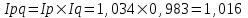 Средняя величина равна 100 рублей, а дисперсия средней величины – 225, чему равен коэффициент вариации? Решение: Среднее квадратическое отклонение: 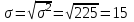 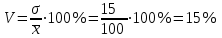 Коэффициент вариации составил 20%, а средняя величина – 33 руб. Чему равно среднее квадратическое отклонение? Решение: 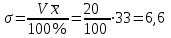 Коэффициент вариации составил 35%, а средняя величина – 70 руб. Чему равна дисперсия? Решение: 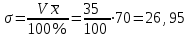 Среднее квадратическое отклонение: 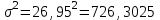 Цены на первый товар в отчетном периоде выросли на 3%, в второй товар – 4%, а на третий цены снизились на 1%. Известно, что в базисном периоде оборот первого товара составил – 100 руб., второго – 150 руб., третий – 95 рублей. Чему равен общий индекс цен? Решение: 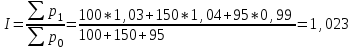 В среднем цены увеличились на 2,3% Цены на первый товар в отчетном периоде выросли на 3%, в второй товар – 4%, а на третий цены снизились на 1%. Известно, что в отчетном периоде оборот первого товара составил – 100 руб., второго – 150 руб., третий – 95 рублей. Чему равен общий индекс цен? Решение: 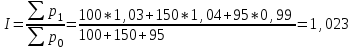 В среднем цены увеличились на 2,3% Ряд динамики состоит из 5 уровней, показатель первого периода – 450 тыс. руб., последнего – 480 тыс. руб. Чему равен средний темп роста? Решение: Средний темп роста равен 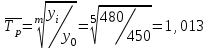 Ряд динамики состоит из 9 уровней. Первый уровень -300 тыс. руб., последний уровень – 270 тыс. руб. Чему равен средний темп роста? Решение: Средний темп роста равен 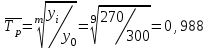 Известно, что общий выпуск продукции на 1 предприятии составил 250 тыс. руб., на втором – 1000 тыс. руб., цена продукции 1 предприятия равна 150 рублей, 2 предприятия – 110 рублей. Чему равна средняя цена по двум предприятиям? Решение: 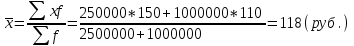 В интервале от 15 до 20 тыс. руб. находилась заработная плата 7 работников, в интервале от 20 до 45 тыс. руб. – 10 работников, в интервале от 45 до 65 тыс. руб. – 10 работников. Чему равна средняя заработная плата всех работников? Решение: Найдем средину интервалов 1)(15+20)/2=17,5тыс.руб. 2)(20+45)/2=32,5тыс.руб. 3) (45+65)/2=55тыс.руб. Средняя заработная плата всех работников составит 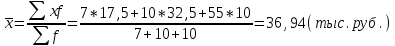 На 1 января товарные запасы оценивались в 250 тыс. руб., на 1 февраля – 275 тыс. руб., на 1 марта – 280 тыс. руб., на 1 апреля – 285 тыс. руб. Чему равен средний уровень товарных запасов в 1 квартале года? Решение: 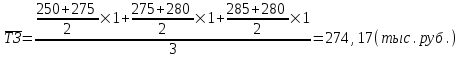 29.На предприятии работают 5 работников с заработной платой 30 т.р. руб., 5 работников с заработной платой 35 т.р., 7 работников с заработной платой 48 т.р. и 4 работника с заработной платой 51 тыс. руб. Чему равна средняя заработная плата на данном предприятии? Решение: 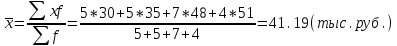 | ||||