информатика 9 класс. Информатика (материал к занятию 21.09.2021). Тема Измерение информации содержательный и алфавитный подходы. Выполните задание в тетради. Заполните пропуски
 Скачать 24.21 Kb. Скачать 24.21 Kb.
|
|
Тема «Измерение информации: содержательный и алфавитный подходы». 1. Выполните задание в тетради. Заполните пропуски: 512 Кбайт = … байт = … бит. … Гбайт = 1536 Мбайт = … Кбайт. … Кбайт = … байт = 12288 бит 5 Кбайт = ... байт = бит 2. Изучите материал темы «Измерение информации: содержательный и алфавитный подходы». Подготовьте в тетради конспект лекции. «Измерение информации: содержательный и алфавитный подходы». Вопрос: «Как измерить информацию?» очень непростой. Ответ на него зависит от того, что понимать под информацией. Но поскольку определять информацию можно по-разному, то и способы измерения тоже могут быть разными. Содержательный подход к измерению информации. Для человека информация — это знания человека. Рассмотрим вопрос с этой точки зрения. Получение новой информации приводит к расширению знаний. Если некоторое сообщение приводит к уменьшению неопределенности нашего знания, то можно говорить, что такое сообщение содержит информацию. Отсюда следует вывод, что сообщение информативно (т.е. содержит ненулевую информацию), если оно пополняет знания человека. Например, прогноз погоды на завтра — информативное сообщение, а сообщение о вчерашней погоде неинформативно, т.к. нам это уже известно. Нетрудно понять, что информативность одного и того же сообщения может быть разной для разных людей. Например: «2x2=4» информативно для первоклассника, изучающего таблицу умножения, и неинформативно для старшеклассника. Но для того чтобы сообщение было информативно оно должно еще быть понятно. Быть понятным, значит быть логически связанным с предыдущими знаниями человека. Определение «значение определенного интеграла равно разности значений первообразной подынтегральной функции на верхнем и на нижнем пределах», скорее всего, не пополнит знания и старшеклассника, т.к. оно ему не понятно. Для того, чтобы понять данное определение, нужно закончить изучение элементарной математики и знать начала высшей. Получение всяких знаний должно идти от простого к сложному. И тогда каждое новое сообщение будет в то же время понятным, а значит, будет нести информацию для человека. Сообщение несет информацию для человека, если содержащиеся в нем сведения являются для него новыми и понятными. Очевидно, различать лишь две ситуации: «нет информации» — «есть информация» для измерения информации недостаточно. Нужна единица измерения, тогда мы сможем определять, в каком сообщении информации больше, в каком — меньше. Единица измерения информации была определена в науке, которая называется теорией информации. Эта единица носит название «бит». Ее определение звучит так: Сообщение, уменьшающее неопределенность знаний в два раза, несет 1 бит информации. Например, после сдачи зачета или выполнения контрольной работы ученик мучается неопределенностью, он не знает, какую оценку получил. Наконец, учитель объявляет результаты, и он получаете одно из двух информационных сообщений: «зачет» или «незачет», а после контрольной работы одно из четырех информационных сообщений: «2», «3», «4» или «5». Информационное сообщение об оценке за зачет приводит к уменьшению неопределенности знания в два раза, так как получено одно из двух возможных информационных сообщений. Информационное сообщение об оценке за контрольную работу приводит к уменьшению неопределенности знания в четыре раза, так как получено одно из четырех возможных информационных сообщений. Неопределенность знаний о некотором событии — это количество возможных результатов события. Рассмотрим еще один пример. На книжном стеллаже восемь полок. Книга может быть поставлена на любую из них. Сколько информации содержит сообщение о том, где находится книга? Применим метод половинного деления. Зададим несколько вопросов уменьшающих неопределенность знаний в два раза. З 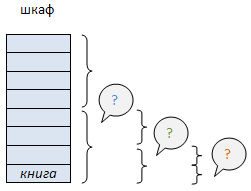 адаем вопросы: адаем вопросы:- Книга лежит выше четвертой полки? - Нет. - Книга лежит ниже третьей полки? - Да. - Книга — на второй полке? - Нет. - Ну, теперь все ясно! Книга лежит на первой полке! Каждый ответ уменьшал неопределенность в два раза. Всего было задано три вопроса. Значит набрано 3 бита информации. И если бы сразу было сказано, что книга лежит на первой полке, то этим сообщением были бы переданы те же 3 бита информации. Если обозначить возможное количество событий, или, другими словами, неопределенность знаний N, а буквой I количество информации в сообщении о том, что произошло одно из N событий, то можно записать формулу: 2I = N Количество информации, содержащееся в сообщении о том, что произошло одно из N равновероятных событий, определяется из решения показательного уравнения: 2I = N. Алфавитный подход к измерению информации. А теперь познакомимся с другим способом измерения информации. Этот способ не связывает количество информации с содержанием сообщения, и называется он алфавитным подходом. При алфавитном подходе к определению количества информации отвлекаются от содержания информации и рассматривают информационное сообщение как последовательность знаков определенной знаковой системы. Проще всего разобраться в этом на примере текста, написанного на каком-нибудь языке. Для нас удобнее, чтобы это был русский язык. Все множество используемых в языке символов будем традиционно называть алфавитом. Обычно под алфавитом понимают только буквы, но поскольку в тексте могут встречаться знаки препинания, цифры, скобки, то мы их тоже включим в алфавит. В алфавит также следует включить и пробел, т.е. пропуск между словами. Полное количество символов алфавита принято называть мощностью алфавита. Будем обозначать эту величину буквой N. Например, мощность алфавита из русских букв и отмеченных дополнительных символов равна 54. Представьте себе, что текст к вам поступает последовательно, по одному знаку, словно бумажная ленточка, выползающая из телеграфного аппарата. Предположим, что каждый появляющийся на ленте символ с одинаковой вероятностью может быть любым символом алфавита. В действительности это не совсем так, но для упрощения примем такое предположение. В каждой очередной позиции текста может появиться любой из N символов. Тогда, согласно известной нам формуле, каждый такой символ несет I бит информации, которое можно определить из решения уравнения: 2I = 54. Получаем: I = 5.755 бит. Вот сколько информации несет один символ в русском тексте! А теперь для того, чтобы найти количество информации во всем тексте, нужно посчитать число символов в нем и умножить на I. Посчитаем количество информации на одной странице книги. Пусть страница содержит 50 строк. В каждой строке — 60 символов. Значит, на странице умещается 50x60=3000 знаков. Тогда объем информации будет равен: 5,755 х 3000 = 17265 бит. При алфавитном подходе к измерению информации количество информации зависит не от содержания, а от размера текста и мощности алфавита. При использовании двоичной системы (алфавит состоит из двух знаков: 0 и 1) каждый двоичный знак несет 1 бит информации. Интересно, что сама единица измерения информации «бит» получила свое название от английского сочетания «binary digit» - «двоичная цифра». Применение алфавитного подхода удобно прежде всего при использовании технических средств работы с информацией. В этом случае теряют смысл понятия «новые — старые», «понятные — непонятные» сведения. Алфавитный подход является объективным способом измерения информации в отличие от субъективного содержательного подхода. Удобнее всего измерять информацию, когда размер алфавита N равен целой степени двойки. Например, если N=16, то каждый символ несет 4 бита информации потому, что 24 = 16. А если N =32, то один символ «весит» 5 бит. Ограничения на максимальный размер алфавита теоретически не существует. Однако есть алфавит, который можно назвать достаточным. С ним мы скоро встретимся при работе с компьютером. Это алфавит мощностью 256 символов. В алфавит такого размера можно поместить все практически необходимые символы: латинские и русские буквы, цифры, знаки арифметических операций, всевозможные скобки, знаки препинания.... Поскольку 256 = 28, то один символ этого алфавита «весит» 8 бит. Причем 8 бит информации — это настолько характерная величина, что ей даже присвоили свое название — байт. 1 байт = 8 бит. Сегодня очень многие люди для подготовки писем, документов, статей, книг и пр. используют компьютерные текстовые редакторы. Компьютерные редакторы, в основном, работают с алфавитом размером 256 символов. В этом случае легко подсчитать объем информации в тексте. Если 1 символ алфавита несет 1 байт информации, то надо просто сосчитать количество символов; полученное число даст информационный объем текста в байтах. Пусть небольшая книжка, сделанная с помощью компьютера, содержит 150 страниц; на каждой странице — 40 строк, в каждой строке — 60 символов. Значит страница содержит 40x60=2400 байт информации. Объем всей информации в книге: 2400 х 150 = 360 000 байт. 3. Выполните в тетради задания. Каково было количество событий, если при реализации одного из них было получено 7 бит информации? Считая, что каждый символ кодируется 8 битами, оцените объем следующего сообщения в байтах: «Mail.ru – почтовый сервер». |
