Тема Методы экспертного оценивания
 Скачать 295.36 Kb. Скачать 295.36 Kb.
|
Тема: Методы экспертного оцениванияРанее были определены два основных метода обобщения числовых показателей объектов по некоторым направлениям (критериям). При этом предполагалось, что все критерии являются количественными и оценки альтернатив по ним получаются в результате простых измерений. Однако, в реальной практике, очень часто критерии являются качественными и не позволяют напрямую измерить объекты, а лишь сравнить их. Методы, посвященные тому, как в таких ситуациях получить количественные оценки объектов по качественным критериям, составляют отдельное направление системного анализа, называемое экспертным оцениванием. Экспертнымоцениваниемназываются математические методы и модели, позволяющие на основании оценок объектов одним экспертом или группой экспертов получить количественные оценки объектов по качественным критериям. Было разработано достаточно много методов получения количественных оценок по качественным критериям. Эти оценки осуществляет либо эксперт (специалист по исследуемому вопросу), либо сам исследователь. Простейшим (и достаточно популярным) является методжюри, согласно которому эксперт просто-напросто, в соответствии со своими знаниями, опытом и интуицией, расставляет баллы для каждого объекта по каждому критерию по заданной шкале. Точно также оцениваются и веса критериев. Однако на практике не всегда можно точно и пропорционально оценить показатели объектов, особенно при большом их числе. Гораздо проще бывает попарно сравнить все имеющиеся объекты по каждому критерию и оценить, насколько один конкретный объект превосходит по критерию другой. Такой метод экспертной оценки получил название методапарныхсравнений. В свою очередь, метод парных сравнений имеет две модификации: методаналитическойиерархиии метод латентных переменных. Рассмотрим математические модели для метода парных сравнений подробно. 1. Экспертное оценивание методом аналитической иерархииПусть имеется n объектов, которые обозначим A1, A2 ,..., An, и m критериев, обозначенные K1, K2 ,..., Km. Возьмем первый критерий K1 и  ij попарно сравним все объекты друг с другом по этому критерию. В результате получим матрицу сравнений V(1) , каждый элемент которой, в случае, если объект Ai не менее предпочтителен по критерию чем объект Aj равен h. Если же объект Ai не более предпочтителен по критерию чем объект Aj, то соответствующий элемент матрицы (1)  V ij равен 1/h. Так же вычисляются матрицы сравнения (k)  V , ij k 1,2,..., m для других критериев. Введем, например, такую шкалу сравнений, какая указана в табл. 1. Таблица 1 Шкалаотносительнойважностипарногосравненияобъектов
При желании можно использовать четные целые числа, выражающие промежуточные уровни предпочтительности. Следует отметить, что эксперт или исследователь может использовать иные другие шкалы важности парных сравнений. Аналогично, попарно сравнивая важности критериев, составляется матрица сравнения критериев по которой можно определять их веса. На следующем этапе вычисляются собственные векторы объектов по всех критериям. Для каждой i-й альтернативы по k-му критерию вычисляем элемент вектора (k)  U i который равен среднегеометрическому показателей матрицы сравнения для этого объекта (строки матрицы): 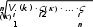 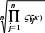  i U(k) . (1) Такой же собственный вектор вычисляется и для матрицы сравнения критериев с целью определения их весов. Далее в результате нормализации собственных векторов вычисляют веса объектов по каждому критерию и веса самих критериев. Вес i-го объекта по k-му критерию Wi(k) равен отношению соответствующего элемента собственного вектора к сумме всех элементов собственного вектора данного критерия: (k) U(k) U(k) Wi i i . (2) n (k) U(k) U(k) ... U(k) Ui 1 2 ni1 Также вычисляются и веса критериев, которые обозначим   W , (k) крит k 1,2,..., m. Теперь, имея оценки объектов по всем критериям и веса критериев можно вычислить функции полезности по каждому объекту по формуле: F mW(k) W(k) W(1) W(1) W(2) W(2) ... W(m) W(m) . (3) i ik1 критi крит i крит i крит Рассмотрим применение метода аналитической иерархии на примере. Пример 1. Предприниматель, занимающейся продажей профессионального оборудования для парикмахерских и косметических салонов решил открыть новую торговую точку и построить магазин в одном из районах города. Городские власти предлагают ему под строительство четыре земельных участка: А, В, С и D. В качестве критериев при выборе места строительства предприниматель выделяет три: -доступностьмагазинадляклиентов(место расположения)– K1; стоимостьстроительства, доступность коммуникаций – K2; возможностьдальнейшегорасширения(планируется со временем пристроить помещения для дополнительных отделов) – K3. Предприниматель, выступая экспертом по первому критерию о доступности и месторасположения магазина сравнил объекты и решил, что А по сравнению с В имеет умеренное преимущество (балл 3), А по сравнению с С имеет значительное превосходство (балл 7) и А по сравнению с D – существенное превосходство (балл 5). Эти баллы записываем в первую строку таблицы. Сравнивая альтернативы В и С, эксперт решил, что В имеет превосходство большее, чем умеренное и менее, чем существенное, поэтому в таблицу на соответствующую позицию было решено занести балл 4. Объект В по сравнению с D имеет умеренное превосходство, а С и D имеют равную важность. В результате, получаем оценки в соответствии с табл. 2. Таблица 2 Критерий«Доступностьмагазинадляклиентов»
По аналогии, эксперты по двум другим критериям сравнили попарно все объекты и получили следующие результаты, которые представлены в табл. 3. Таблица 3 Критерий«Стоимостьстроительства»
Критерий«Возможностьрасширения»
Следующий этап состоит в сравнении важностей самих критериев. Предприниматель считает самым важным первый критерий, он имеет умеренное превосходства над вторым и существенное над третьим. Второй критерий имеет умеренное превосходство над третьим. В результате получаем матрицу, приведенную в табл. 4. Таблица 4
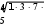 Третий этап состоит в расчете собственных векторов и весов объектов по каждому критерию. Для первого критерия «Доступностьмагазинадля Третий этап состоит в расчете собственных векторов и весов объектов по каждому критерию. Для первого критерия «Доступностьмагазинадляклиентов»собственный вектор объекта А равен 3,201, Для 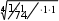 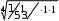 второго, третьего и четвертого объекта собственные вектора равны: второго, третьего и четвертого объекта собственные вектора равны: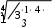 1,414 , 1,414 ,соответственно. 0,435 и 0,508 Рассчитаем теперь веса объектов. Просуммируем элементы собственного вектора: 3,202 1,414 0,435 0,508 5,559. Разделим каждый элемент собственного вектора на эту сумму, получим нормализованные веса каждого объекта, а именно, для объекта А: 3,202/5,559=0,576, для других объектов, аналогично, 0,254, 0,078, 0,092. Следует отметить, что в сумме веса должны давать единицу. Запишем результат в табл. 4. Таблица 4 Критерий«Доступностьмагазинадляклиентов»
сумма 5,559 Аналогичные таблицы составляем и для случая парного сравнения объектов по другим критериям, которые приведены в табл. 5. Таблица 5 Критерий«Стоимостьстроительства»
сумма 5,452 Критерий«Возможностьрасширения»
сумма 5,550 Таким же способом вычисляем собственные вектора и веса критериев. Единственное отличие при вычисление собственных векторов состоит в том, что число критериев равно трем (а число альтернатив – четыре), поэтому из произведения парных оценок сравнений нужно брать корень третьей степени. Например, для критерия K1: 3.6. 2,466 . Результаты – в табл. 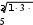 Таблица 3.5 Таблица 3.5
сумма 3,871 Рассчитываем функции полезности для каждого объекта: F1 0,576 0,637 0,128 0,258 0,111 0,105 0,423; F2 0,254 0,637 0,057 0,258 0,07 0,105 0,184; F3 0,078 0,637 0,517 0,258 0,298 0,105 0,211; F4 0,092 0,637 0,298 0,258 0,521 0,105 0,182; Видно, что максимальная функция полезности соответствует первому объекту А, следовательно, данный участок и следует выбрать для строительства. |
