Главная страница
Навигация по странице:

  • =ТРАНСП(A9:A12)

  • =СУММ(G2:J5)

  • =СУММ(F3:F6).

    		•

    Тема Методы экспертного оценивания


    Скачать 295.36 Kb.
    НазваниеТема Методы экспертного оценивания
    Дата25.03.2023
    Размер295.36 Kb.
    Формат файлаdocx
    Имя файлаExp_oc.docx
    ТипДокументы
    #1014449
    страница6 из 7
    1   2   3   4   5   6   7

    =(В12-МИН($В$12:$I$12))/(МАКС($В$12:$I$12)-МИН($В$12:$I$12)).


    Автозаполняем на В33-I33. Результаты расчетов приведены ниже:

    Рассчитанные

    оценки i
    0,85194
    0,84749
    1,10043
    1,10038
    0,94962
    1,05009
    1,05075
    1,04927

    Нормированные

    оценки i
    0,01761
    0,0000
    1,0000
    0,9998
    0,4038
    0,8010
    0,8036
    0,7977

    Наилучшие оценки получили проекты А3 и А4 (у А3 чуть выше), наихудшую оценку А2. Для многокритериальной задачи аналогично проводится оценка проектов по всем критериям и оцениваются важности самих критериев.

    Часть 2. Принятие решения для многокритериальной задачи


    Обобщим материал, приведенный в Части 1, на случай нескольких критериев и рассмотрим методику оценки объектов. Метод парных сравнений является одним из наиболее точных методов, которые позволяют

    произвести оценки объектов по критериям и найти оценки весов критериев. Рассмотрим способ решения задачи выбора лучшего проекта на ЭВМ на примере.

    ПРИМЕР 2. Необходимо выбрать лучший проект электропроводки в здании из четырех: А, В, C и D. В качестве критериев выбора выступают: Электробезопасность (К1), Пожарная безопасность (К2), Удобство в обслуживании (К3) и Надежность (К4). Все критерии качественные и результате экспертных оценок матрицы парных сравнений проектов по каждому критерию и критериев между собой имеют вид:

    Объекты (проекты)


    K1
    A
    B
    C
    D
    K2
    A
    B
    C
    D

    A
    0,5
    0,6
    0,2
    0,7
    A
    0,5
    0,2
    0,6
    0,4

    B
    0,4
    0,5
    0,4
    0,6
    B
    0,8
    0,5
    0,7
    0,4

    C
    0,8
    0,6
    0,5
    0,3
    C
    0,4
    0,3
    0,5
    0,7

    D
    0,3
    0,4
    0,7
    0,5
    D
    0,6
    0,6
    0,3
    0,5

    K3
    A
    B
    C
    D
    K4
    A
    B
    C
    D

    A
    0,5
    0,9
    0,5
    0,4
    A
    0,5
    0,9
    0,2
    0,4

    B
    0,1
    0,5
    0,2
    0,6
    B
    0,1
    0,5
    0,7
    0,4

    C
    0,5
    0,8
    0,5
    0,7
    C
    0,8
    0,3
    0,5
    0,6

    D
    0,6
    0,4
    0,3
    0,5
    D
    0,6
    0,6
    0,4
    0,5

    Критерии
    К1
    К2
    К3
    К4

    К1
    0,5
    0,6
    0,7
    0,2

    К2
    0,4
    0,5
    0,3
    0,7

    К3
    0,3
    0,7
    0,5
    0,8

    К4
    0,8
    0,3
    0,2
    0,5


    Откроем программу MS EXCEL. Введем исходные данные. Подготовим также поля для собственных векторов и весов, а также поля для вычисления функции полезности альтернатив. Полученная картина в листе электронной таблицы должна быть такая же, как на рисунке.


    Для вычисления собственных векторов (столбцы F и М) необходимо пять раз решать задачу, аналогичную той, которая описана в Части 1. Рассмотрим еще раз ее решение для первой матрицы.

    Переходим на Лист 2, подготавливаем данные как на рисунке (значения в В2-Е5 можно скопировать с первой матрицы из Листа 1).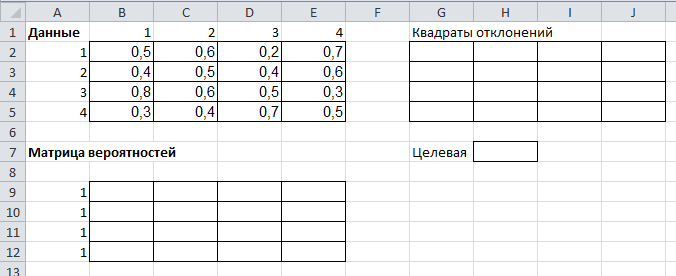



    Ставим курсор в В8, вводим функцию =ТРАНСП(A9:A12), выделяем мышью ячейки В8-Е8, нажимаем F2 и потом одновременно Ctrl+Shift+Enter. Ставим курсор в В9, вводим =EXP($A9-B$8)/(1+EXP($A9-B$8)). Автозаполняем на В9-Е12. Ставим курсор в G2, вводим формулу =(B2-B9)^2, автозаполняем на G2-J5. Ставим курсор в Н7, вводим формулу

    =СУММ(G2:J5). Вызываем надстройку «Поиск решений», оптимизируем целевую Н7 до минимума, в поле «Изменяя ячейки переменных» указываем ссылку на А9-А12. Без дополнительных ограничений, нажимаем сразу

    «Найти решение». В ячейках А9-А12 получаем значения собственного вектора для первого критерия. Копируем эти значения с Листа 2 и вставляем на Лист 1 в ячейки F3-F6.

    Проделываем эту же процедуру для критерия К2. Переходим на Лист 3. Чтоб не набирать все заново, можно скопировать данные с Листа 2, изменив


    ∑
    затем В2-Е5 и поставив единицы в А9-А12. Запускаем надстройку. Данные из А9-А12 копируем на первый лист. То же делаем и для критериев К3 и К4 и весов критериев (матрица I3-L6). Далее вычисляем сумму элементов векторов. Переходим на Лист 1, Ставим курсор в F7 и нажимаем кнопку вызывая мастер автосумм, обводим мышкой ячейки F3-F6, указав, какие ячейки просуммировать. Результат должен выглядеть так: =СУММ(F3:F6). Аналогично в ячейке F13 выводим сумму F9-F12 =СУММ(F8:F12), в ячейке F19 выводим сумму F15-F18 =СУММ(F15:F18), в ячейке F25 выводим сумму F21-F24 =СУММ(F21:F24), в ячейке М7 выводим сумму М3-М6
    1   2   3   4   5   6   7

    написать администратору сайта