Методичекое пособие по математике 2011. Тема Представления о множествах Интуитивные представления (Элемент, принадлежность, равенство, интуитивный принцип объемности)
 Скачать 231.99 Kb.
|
|
Докажем несколько утверждений общего характера о тавтологиях. 1. Если А, (А В) - тавтологии, то тавтологией является В. Предположим , что В не является тавтологией. Тогда В принимает значение “ложь” при некотором наборе значений пропозиционных переменных. Но при этом же наборе значений переменных А имеет значение “истина”, так как А - тавтология (по условию). В таблице истинности такому набору значений А и В импликации (А В) соответствует значение “ложь”. Получили противоречие с условием, что (А В) - тавтология. 2. Если А - тавтология, содержащая пропозиционные переменные А1, А2 , ... , Аn , и В получается из А подстановкой формул Ф1, Ф2 , ... , Фn вместо А1, А2 , ... , Аn соответственно, то В есть тавтология, т.е. подстановка в тавтологию есть тавтология. Доказательство: Обозначим А = А (А1, А2 , ... , Аn ), тогда В символически запишется В = А (Ф1, Ф2 , ... , Фn ). Нам нужно показать, что 1) В - формула; 2) В - тавтология. Первое следует из определения формулы и из того, что Ф1, Ф2 , ... , Фn - формулы. Пусть задан некоторый набор значений для пропозиционных переменных формулы В. Формулы Ф1, Ф2 , ... , Фn примут тогда некоторые значения х1, х2 , ... , хn (каждое хk есть И или Л). Если мы придадим значения х1, х2 , ... , хn соответственно пропозиционным переменным А1, А2 , ... , Аn, то значение А совпадет с истинностным значением В при заданном распределении значений пропозиционных переменных, входящих в В. Так как А по условию тавтология, то В при этом наборе значений переменных примет значение “истина”. Таким образом, В всегда принимает значение И, т.е. является тавтологией. Пример 2. Формула F=(A(BA)) является тавтологией. Действительно, если предположить ,что F принимает значение Л, то А - И, а ( В А) - Л. Но импликация (В А) принимает значение Л только в том случае, когда В - И , а А - Л. Получили противоречие с тем, что А - И. Рассмотрим формулы Ф1 = С& A и Ф2 = ((С) А). Заменим в формуле F пропозиционную переменную А на Ф1 , а В на Ф2 , соответственно. Получим новую формулу F*= ((С& A) (((С) А) (С& A))), которая является тавтологией. Убедимся в этом, составив для нее таблицу истинности.
Если в формуле F заменить только А на Ф1 , то получим еще одну тавтологию F** = = ((С& A) (B (С& A))).
Полные системы связок. В этом разделе мы рассмотрим множество логических связок с точки зрения взаимозаменяемости его элементов. Наша задача, выбрать такое минимальное подмножество, с помощью которого можно будет определить все остальные логические связки. Такое подмножество называется полным. Определение 3. Две формулы F и Ф ( F = Ф ) называются логическиэквивалентными ( равносильными), если ( F Ф ) - тавтология. Из определения следует, что F равносильна Ф тогда и только тогда, когда в таблице истинности соответствующие столбцы совпадают. Покажем, что формула (А В) равносильна формуле ((А) В).
Равносильность ( 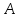 В) = ((А) В) показывает, что связку можно исключить, заменив ее связками и . Связку & можно исключить в силу равносильности (А & В) = ((А) (В)). Так как (А В) = ((А В) & (В А)), а связки и & можно выразить через отрицание и дизъюнкцию, то связка так же может быть исключена. Это показывает, что система связок { , } полна.Решение задач по теории множеств с помощью таблиц истинности. Если на выражения х А, у В посмотреть как на элементарные высказывания, то каждая формула теории множеств может быть заменена формулой логики высказываний. Это позволяет метод таблиц истинности применить к решению задач по теории множеств. Сведем этот способ решения задач к таблице.
Например, докажем равенство (А В) = (А \ В ). Переведем это равенство в доказательство равносильности формул ((А) В) = ( 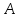В), для чего воспользуемся таблицей истинности на предыдущей странице, показывающей их равносильность.КОНТРОЛЬНЫЕ ЗАДАНИЯ ИЗБРАННЫЕ ВОПРОСЫ МАТЕМАТИКИ МАТЕМАТИЧЕСКАЯ ЛОГИКА КОНТРОЛЬНАЯ РАБОТА № 3 ВАРИАНТ № 1 ЗАДАЧА 1. Записать следующие сложные высказывания в виде логических формул, обозначая элементарные васказывания буквами : а) если я не пойду в гости, то успею решить задачу и приготовить обед; б) студент получит зачет тогда только тогда, когда решит все три или две задачи. ЗАДАЧА 2. В выражении А В В А С расставить скобки всеми возможными способами так , чтобы получилась формула. ЗАДАЧА 3. Составить таблицу истинности для формулы F=((( A ) (BC)) A). ЗАДАЧА 4. Доказать тождественную истинность следующих формул : а) (((А В) ) ( (А )( В))); б) ( ((А) ( В)) (В А)). ЗАДАЧА 5. Решить задачу 5 из контрольной работы № 1, используя логические формулы. ЗАДАЧА 6. Доказать эквивалентность формул (А (В С)) и ((А В) (А С)). ЗАДАЧА 7. Доказать полноту логических связок: , . ВАРИАНТ № 2 ЗАДАЧА 1. Записать следующие сложные высказывания в виде логических формул, обозначая элементарные васказывания буквами : а) если Петя пойдет в кино или на тренировку, то он не успеет выполнить домашнее задание; б) шейх счастлив тогда и только тогда, когда имеет вино и услаждает свой слух пением. ЗАДАЧА 2. В выражении А С А В С расставить скобки всеми возможными способами так , чтобы получилась формула. ЗАДАЧА 3. Составить таблицу истинности для формулы F=((A ((BC))). ЗАДАЧА 4. Доказать тождественную истинность следующих формул : а) (А ( (А В) ( А ( В)))); б) (А (В (А В ))). ЗАДАЧА 5. Решить задачу 5 из контрольной работы № 1, используя логические формулы. ЗАДАЧА 6. Доказать эквивалентность формул ((А В) ) и ( (А )( В)); ЗАДАЧА 7. Доказать полноту логических связок: , . ВАРИАНТ № 3 ЗАДАЧА 1. Записать следующие сложные высказывания в виде логических формул, обозначая элементарные васказывания буквами : а) Петя ходит в кино тогда и только тогда, когда там показывают комедию или детектив; б) если мистер Джонс счастлив, то миссис Джонс несчастлива, и если мистер Джонс несчастлив, то миссис Джонс счастлива. ЗАДАЧА 2. В выражении А С А В С расставить скобки всеми возможными способами так , чтобы получилась формула. ЗАДАЧА 3. Составить таблицу истинности для формулы F=(A ((B(CА)))). ЗАДАЧА 4. Доказать тождественную истинность следующих формул : а) (((А В)) ( (А) ( В))); б) (( (А В) А ) А ). ЗАДАЧА 5. Решить задачу 5 из контрольной работы № 1, используя логические формулы . ЗАДАЧА 6. Доказать эквивалентность формул (А (В С)) и ((А В) (А С)). ЗАДАЧА 7. Доказать полноту логических связок: , . АКСИОМАТИЧЕСКОЕ ПОЛЕ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ Рассмотрим множество элементов. На нем заданы две бинарные операции, одну из которых назовем сложением, а другую умножением. И пусть на этом множестве задано отношение порядка. Пусть само множество, операции и отношения на нем обладают следующими свойствами: Операция сложения. Обозначим ее “+”. 1) а и b: a + b = b + a (коммутативное свойство); 2) a, b и c: a+ (b + c) = (a + b) + c (ассоциативное свойство); 3) число 0, для а: а + 0 = а (существует нейтральный элемент по сложению, который называется ноль или нуль и который обозначим через 0); 4) а, b: а + b = 0, b называется противоположным числом к а. Будем обозначать его (- b). Операция умножения. Обозначим ее “*”. 1) а, b: ab = ba (коммутативное свойство); 2) a, b и c: a(bc) = (ab)c(ассоциативное свойство); 3) элемент (обозначим его 1) такой, что для а 0: а1 = а (существование нейтрального элемента по умножению) 4) а 0, b: ab = 1 (существование обратного элемента), где элемент b обозначим как а-1 или (1/а). 3. Операции сложения и умножения связаны свойством дистрибутивного (распределительного) закона: a, b и c: (a + b)c = aс +bc. Упражнение: Доказать, что а0 = 0. 4. Упорядоченность. Бинарное отношение ≥ является отношением линейного порядка, т.е. отношение “” обладает свойствами: 1) рефлексивность; aи b из того, что a b и a b a = b (антисимметричность); 3) a и b, a b и b c a с (транзитивность), кроме того, операция сложения связана с тем, что для a, b, c и a b a + c b + c; a, b и из того, что a 0, b 0 ab 0. 5. Аксиома Архимеда. a, b, n, что na > b. Эта аксиома позволяет утверждать, что ни при каких n n*1 0. Определение 1 два множества АR и BR называются сечением множества действительных чисел R, если: 1) R(т.е. каждое действительное число принадлежит хотя бы одному из множеств А и В); 2) и ; 3) каждое число множества А меньше любого числа множества В: если а, bВ, то a < b(из этого свойства следует, что , т.к. если бы нашелся такой х х и х , то из 3) следовало бы, что х < х). Множество А называется нижним, а В – верхним классом данного сечения. Пример. Зафиксируем какое-либо число R, отнесем сначала к множеству А все числа х , а к множеству В – все числа y > : А = {x: х }, B = {y: y > } (1). Можно поступить иначе: отнести к множеству А все числа х < , а к множеству В – все числа y : А = {x: х < }, B = {y: y } (2). В обоих случаях А и В образуют сечения. Сечение производится некоторым числом и записывают в виде . Отметим два свойства сечений производящихся некоторым числом: 1. В случае (1) в классе А есть наибольшее число, им является число , а в классе В нет наименьшего числа. В случае (2) в классе А нет наибольшего, а в классе В есть наименьшее число, им является число . 2. Число, производящее сечение, единственно. 6. Непрерывность. Для каждого сечения АВ множества действительных чисел число , производящее это сечение, . Свойство непрерывности состоит в том, что никаких других сечений действительных чисел, кроме тех, которые производятся некоторым числом, не существует. |