Методичекое пособие по математике 2011. Тема Представления о множествах Интуитивные представления (Элемент, принадлежность, равенство, интуитивный принцип объемности)
 Скачать 231.99 Kb. Скачать 231.99 Kb.
|
Рис. 1Для любых подмножеств А, В и С универсального множества U выполняются следующие тождества: 1. Коммутативность: А В = В А ; А В = В А ; 2. Ассоциативность: А (В С) = (А В) С; А (В С) = (А В) С; 3. Дистрибутивность: А (В С) = (А В) (А С); А (В С) = (А В) (А С); 4. А = А, А U = U; А = , А U = А; 5. А А = U ; А А = ; 6. Идемпотентность: А А = А; А А = А; 7. Законы де Моргана: 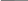  А В = А В; А В = А В; А В = А В; А В = А В;8. Закон поглощения: А (А В) = А; А (А В) = А. Докажем тождество 3: А (В С) = (А В) (А С). Обозначим М = А (В С) и N = (А В) (А С). Равенство M = N равносильно () двум включениям: М N , N M. Сначала докажем, что М N . Пусть х М = А (В С). Это означает, что х А или х В С. Если х А, то х А В и х А С. Следовательно, х (А В) (А С) = N. Первое включение доказано. Покажем, что N M. Пусть х N = (А В) (А С), тогда х А В и х А С. Следовательно, либо х А, и тогда очевидно, что х А (В С), либо х В и х С, т.е. х В С, а значит х А (В С)= М. Докажем тождество 7:А В = А В. П  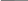 усть х А В. Тогда х А В. Следовательно, х А , х В. Это означает, что хА, х В, т.е. х А В. Итак, А В А В. Пусть теперь х А В. Тогда хА и х В, следовательно, х А, х В. Значит, х А В, т. е. х А В. Итак, А В А В. Тождество доказано. усть х А В. Тогда х А В. Следовательно, х А , х В. Это означает, что хА, х В, т.е. х А В. Итак, А В А В. Пусть теперь х А В. Тогда хА и х В, следовательно, х А, х В. Значит, х А В, т. е. х А В. Итак, А В А В. Тождество доказано.Остальные тождества доказываются аналогично. Упражнение: Докажите оставшиеся тождества. Самостоятельная работа о разделу. 1. Задать 2 – 3 вопроса по каждой теме. Подготовить короткую презентацию с ответами на эти вопросы и с решением упражнений. 2. Подготовить реферат по теме Объекты и их признаки (ключевые слова: предмет, объект, вещь, признак, качество, свойство, объем признака, абстрактный признак, моделирование признака множеством). КОНТРОЛЬНЫЕ ЗАДАНИЯ ТЕОРИЯ МНОЖЕСТВ КОНТРОЛЬНАЯ РАБОТА № 1 ВАРИАНТ № 1 Задача 1. Задать перечислением всех элементов множество А, заданное с помощью характеристического свойства (формы от х) : А = { x | x Z, |x| 2 }. Можно ли задать это множество перечислением, если условие x Z заменить условием x Q? ( Z - множество целых чисел, Q - множество рациональных чисел ). Задача 2. Доказать, что существует лишь одно множество, не имеющее элементов. Задача 3. Определить отношение между множествами прямоугольников и параллелограммов с равными диагоналями. Задача 4. Доказать, что если множество А состоит из n элементов, то множество всех его подмножеств S(A) состоит из 2n элементов. Задача 5. Доказать следующие тождества : а) ( А В) (А В) = ( А В) (А В) = А ; б) (А В) \ С = (А \ С) (В \ С). Проиллюстрировать эти задачи диаграммами Эйлера - Венна. Задача 6. Доказать, что (А В) С А С и В С. Задача 7. Определить операции пересечения, объединения и разности ( , , \ ) множеств через операции симметрической разности и пересечения ( , ). Задача 8. Решить систему уравнений : А Х = В ; А Х = С , где А, В и С - данные множества; В А С. КОНТРОЛЬНЫЕ ЗАДАНИЯ ТЕОРИЯ МНОЖЕСТВ ВАРИАНТ № 2 Задача 1. Задать перечислением всех элементов множество А, заданное с помощью характеристического свойства (формы от х) : А = { x | x Z, |x| 3 }. Можно ли задать это множество перечислением, если условие x Z заменить условием x Q? ( Z - множество целых чисел, Q - множество рациональных чисел ). Задача 2. Доказать, что Задача 3. Определить отношение между множествами ромбов и четырехугольников с равными диагоналями. Задача 4. Доказать, что если множество А состоит из n элементов, то множество всех его подмножеств S(A) состоит из 2n элементов. Задача 5. Доказать следующие тождества : а) (А В) А = А В ; б) А \ ( В С) = (А \ В) \ С. Проиллюстрировать эти задачи диаграммами Эйлера - Венна. Задача 6. Доказать, что А ( В С ) А В и А С. Задача 7. Определить операции пересечения, объединения и разности ( , , \ ) множеств через операции симметрической разности и объединения ( , ). Задача 8. Решить систему уравнений : А \ Х = В ; Х \ А = С , где А, В и С - данные множества; В А и А С = КОНТРОЛЬНЫЕ ЗАДАНИЯ ТЕОРИЯ МНОЖЕСТВ ВАРИАНТ № 3 Задача 1. Задать перечислением всех элементов множество А, заданное с помощью характеристического свойства (формы от х) : А = { x | x Z, |x| 3 }. Можно ли задать это множество перечислением, если условие x Z заменить условием x Q? ( Z - множество целых чисел, Q - множество рациональных чисел ). Задача 2. Доказать, что { {1,2} , {2,3} } { 1,2,3 }. Задача 3. Определить отношение между множествами прямоугольников и четырехугольников с равными диагоналями. Задача 4. Доказать, что если множество А состоит из n элементов, то множество всех его подмножеств S(A) состоит из 2n элементов. Задача 5. Доказать следующие тождества : а) ( А В) В = А В ; б) А \ ( В С ) = (А \ B) (A \ С). Проиллюстрировать эти задачи диаграммами Эйлера - Венна. Задача 6. Доказать, что (А В) С А (В С ). Задача 7. Определить операции пересечения, объединения и разности ( , , \ ) множеств через операции разности и симметрической разности ( \, ). Задача 8. Решить систему уравнений : А \ Х = В ; А Х = С , где А, В и С - данные множества; В А С. Тема 1.2. Введение в математическую логику Согласно одному из самых распространенных определений, логика есть анализ методов рассуждений. Изучая эти методы, логика интересуется в первую очередь формой, а не содержанием доводов в том или ином рассуждении. Логику не интересует истинность или ложность отдельных посылок или заключений, она лишь желает знать, вытекает ли истинность заключения из истинности посылок. Одна из основных задач логики – систематическая формализация и каталогизация правильных способов рассуждений. Математическая логика, как любая другая математическая дисциплина предметом своего изучения имеет математическую модель, в данном случае - модель человеческих рассуждений и правил умозаключений. И как всякая модель она и адекватна, и не совпадает с самой содержательной логикой. Исчисление высказываний (Семантика, синтаксис). Элементарные высказывания. Логические связки. Формулы. В содержательной логике под высказыванием понимается законченная мысль. Это может быть некоторое предложение, о котором имеет смысл говорить истинно оно или ложно, или несколько предложений, связанных между собой определенным образом. Таким образом, можно выделить элементарные высказывания (первокирпичики) и более сложные высказывания, которые по определенным правилам строятся из элементарных. В математической логике элементарные высказывания моделируются элементами некоторого произвольного множества. Пусть М - некоторое множество, его элементы будем называть элементарными высказываниями, и обозначать, как это принято в математической логике, большими латинскими буквами (иногда с индексами). Само множество М = {A, B, C, ... , A 1, ... , A i, ...} будем называть множеством элементарных высказываний. При анализе способов построения сложных высказываний в разговорной речи можно выделить основные связки: “не”, “и”, “или”, “если ..., то...”, “тогда и только тогда” и др. В математической модели им соответствует другое множество, элементы которого называются логическими (пропозициональными) связками. Множество логических связок включает в себя следующие связки : - отрицание (читается: “не”), & () - конъюнкция (“и“), - дизъюнкция (“или”), - импликация (“если..., то ...”), - эквивалентность (“тогда и только тогда”). Кроме того, в математической логике используются и другие связки, в частности, - квантор всеобщности (“каждый”, “любой”, “всякий”), - квантор существования (“существует”, “найдется”). Множество элементарных высказываний и множество логических связок никогда не пересекаются. Теперь мы должны формализовать правила построения сложных высказываний из элементарных. Из множества элементарных высказываний М с помощью множества логических связок построим новое множество Ф, которое будем называть множеством формул. Правило построения множества Ф состоит из 3-х условий ( такой способ определения называют индуктивным). Определение 1. Множество Ф является множеством формул, если выполняются следующие условия: 1) всякое элементарное высказывание есть формула, (М Ф); 2) если F1 и F2 - формулы (F1 , F2 Ф), то ( F1), (F1 & F2), (F1 F2), (F1 - F2), (F1 F2) - формулы; 3) других формул нет. В качестве примера выясним, является ли высказывание А(В) формулой ? Это не элементарное высказывание (в его записи присутствуют логические связки), следовательно, по условию 1) оно не может быть формулой. Так как А и В - элементарные высказывания, то по условию 1) это формулы, тогда (В) - формула по условию 2). Но само выражение А (В) формулой не является, так как не заключено в скобки (сравните с условием 2), а условие 3) утверждает, что других формул нет. Таким образом, по формальным основаниям указанное выражение формулой не является. Значения формул. Таблицы истинности. Теперь рассмотрим высказывания с точки зрения их истинностных значений. В содержательной логике под высказыванием подразумевается повествовательное предложение, о котором можно определенно сказать истинно оно или ложно. Например, предложение “ квадрат является ромбом” - высказывание, причем истинное, а предложение “рассмотрим множество всех функций” высказыванием не является, так как нельзя с определенностью утверждать, истинно оно или ложно. Таким образом, в нашей математической модели каждое элементарное высказывание нужно рассматривать как переменную величину (пропозиционную переменную), которая принимает только два значения “истина” и “ложь”. Значение “истина” принято обозначать через единицу - 1, а “ложь” через ноль - 0. Итак, всякое элементарное высказывание (пропозиционная переменная) формально может принимать одно из значений: 1или 0. Формулы логики высказываний, которые мы определили, выше являются высказываниями, следовательно, тоже должны принимать одно из истинностных значений. Для формул, которые являются таковыми по условию 1), мы уже приняли соглашения (элементарные высказывания). Чтобы определить истинностное значение любой формулы из условия 2), нужно, прежде всего, определить значения формул: А, (А & В), (А В), (А В), (А В) в зависимости от значений входящих в них элементарных высказываний. Это делается с помощью, так называемой таблицы истинности.
Логические связки отрицание, конъюнкцию, дизъюнкцию, импликацию, эквивалентность можно рассматривать как функции, которые определены на двуэлементном множестве {0, 1} со значениями в этом же множестве. Их называют логическими (булевыми) функциями или операциями. Операция отрицания - унарная, а все остальные - бинарные. Таблицу истинности для каждой из операций можно рассматривать как определение этой операции. Из определения формулы следует, что с помощью таблицы истинности можно определить истинностные значения любой формулы. Рассмотрим это на примере. Пример 1. Найти истинностные значения формулы F = ((A B) (( A) & B)). Убедимся, что F формула. Так как А и В - формулы, то (A), (A B) - формулы по условию 2). Тогда в силу этого же условия формулами являются ((A) & B) и F = ((A B) (( A) & B)). Рассмотренные нами выше составные части формулы F, которые сами являются формулами, называются подформуламиформулы F. Для нахождения всех истинностных значений формулы F последовательно найдем значения подформул. Представимы эти вычисления в виде общей таблицы истинности.
Тавтологии. Среди всех логических формул особый интерес представляют такие, которые истинны уже в силу одной только своей функционально- истинностной структуры. Такую формулу можно рассматривать как модель логического закона. Определение 2. Формула А называется тавтологией (тождественно-истинной формулой), если при любых значениях пропозициональных переменных она принимает значение “истина” (1). С помощью таблицы истинности тавтологию можно определить как формулу, для которой соответствующий ей в таблице столбец целиком состоит из 1. Таким образом, построение таблицы истинности это эффективная процедура для решения вопроса о том, является ли данная формула тавтологией. Из таблицы истинности для импликации очевидно следует, что при любых значениях пропозиционной переменной А формула (А А) принимает значение 1, т.е. является тавтологией. Из определения конъюнкции легко получаем, что формула (&()) всегда принимает значение 0 (“ложь”). Тогда формула ((&())) принимает только одно значение -1 (“истина”), т.е. является тавтологией. В данном примере мы встретились с формулой ( & ()), которая всегда принимает значение Л. Такие формулы называют противоречиями (тождественно-ложными формулами). Очевидно, что формула А является тавтологией тогда и только тогда, когда формула () - противоречие. |
