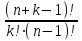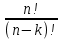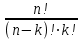Методичекое пособие по математике 2011. Тема Представления о множествах Интуитивные представления (Элемент, принадлежность, равенство, интуитивный принцип объемности)
 Скачать 231.99 Kb. Скачать 231.99 Kb.
|
Двоичная система счисления.Самая часто употребимая система счета – это счет двойками. За основу взято число два. Две единицы образуют уже второй разряд – разряд двоек, две двойки – это третий разряд – разряд четверок. Следующий разряд – это четверки и т.д. Число в двоичной системе изображается только двумя цифрами – единицей и нулем. Единица второго разряда – это два. Единица третьего разряда – четыре, (т.к. 2*2 = 4). Единица четвертого разряда – восемь (2*2*2 = 8), пятого – 8*2 = 16 и т.д. Примеры: В двоичной системе число 101 – это не сто один как в десятеричной. В этом числе последняя цифра – разряд единиц – один. Ноль показывает, что второго разряда нет, т.е. двоек, нет. Первая в числе единица – это единица третьего разряда, т.е. четверка; следовательно, 101 – это 4 + 0 + 1 = 5. А в числе 1110 по двоичной системе единиц ноль, т.е. их нет. Во втором разряде – одна двойка, в третьем – одна четверка, в четвертом – цифра 1 означает, что в этом случае ее надо принять за 8. Все число составит 8 + 4 + 2 + 0 = 14. Вычисления в такой системе счисления самые простые, но требуют длинных записей, на что тратится много времени. Упражнения: Какое самое большое число можно записать тремя цифрами в десятеричной системе счисления, в двоичной системе счисления? Сколько необходимо цифр для того, чтобы записать все двузначные цифры? Постройте пятеричную систему счисления? Контрольные вопросы: Сформулируйте теорему о делении натуральных чисел с остатком, а теперь воспользуйтесь этим алгоритмом и разделите два любых натуральных числа. Сформулируйте теорему о разложении натурального числа. Что мы называем позиционной записью числа? Какие еще системы счисления вы знаете? Контрольные задачи: Доказать, что свойство непрерывности действительных чисел равносильно следующему: каковы бы ни были непустые множества А R, В R, у которых для любых элементов а А, b B выполняются неравенства а b, существует такое число , что для всех а А иb B имеет место соотношение а b. Опишите процесс измерения длины отрезка, если отчет о нем представляется дробью:
Известно, что любое число можно изобразить точкой на числовой прямой. Исчерпывают ли точки с рациональными координатами всю координатную прямую? А точки с действительными координатами? Посчитайте, какова толщина листа бумаги. Сделайте простую линейку для деления величин на целое число частей, в пределах 10. Вычислите несколько знаков бесконечной десятичной дроби, изображающей число  . .Доказать, что между любыми двумя различными действительными числами имеется рациональное число. Доказать, что неравенство 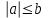 эквивалентно соотношениям эквивалентно соотношениям 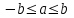 . .Доказать, что для любых двух действительных чисел а и b справедливо неравенство 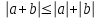 . . Решить уравнение 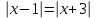 , используя числовую ось. , используя числовую ось.Обладают ли операции вычитания и деления свойствами коммутативности и ассоциативности? Может ли сумма рационального и иррационального чисел числом рациональным? Может ли сумма двух рациональных чисел быть рациональным числом? 4.1. АКСИОМАТИКА НАТУРАЛЬНЫХ ЧИСЕЛ Наряду с геометрией арифметика является наиболее непосредственно интуитивной областью математики. Вполне естественно, поэтому именно с арифметики начать попытку формализации и строгого обоснования математики. Первое полуаксиоматическое построение этой дисциплины было предложено Дедекиндом (1901) и стало известно под названием “системы аксиом Пеано”. Эту систему можно сформулировать следующим образом: 1 есть натуральное число; для любого натурального числа х существует другое натуральное число, обозначаемое х и называемое: (непосредственно) следующее за х; 1 х для любого натурального числа; если х = y, то х = y; если Q есть свойство, которым, быть может, обладают одни и не обладают другие натуральные числа, и если натуральное число 1 обладает свойством Q; для всякого натурального числа х из того, что х обладает свойством Q, следует, что и натуральное число х обладает свойством Q, то свойством Q обладают все натуральные числа (принцип математической индукции). Так выстроенная аксиоматика позволяет моделировать натуральные числа как потенциальную бесконечность, как возможность. В этом смысле натуральные числа могут быть рассмотрены как порядковые числа, то есть моделируются как представители: первый, второй, третий и т.д., в отличие от моделирования количественных представлений. К этому вопросу мы вернемся в последующих параграфах. Контрольные вопросы: Сформулируйте систему аксиом Пеано (Дедекинда). Для чего она необходима? В чем состоит принцип математической индукции? Определите множество натуральных чисел как вполне упорядоченное кольцо. Что такое порядковый тип числа? Постройте модель натурального числа. В чем заключается двойственная природа чисел? Контрольные задачи: Сформулируйте определение отношения a > b и докажите, что оно транзитивно и антисимметрично. Докажите, что если a,b, c – натуральные числа, то:
3. Опишите в общем виде процесс доказательства методом математической индукции. Из скольких этапов он состоит? Используя метод математической индукции, докажите, что для любого натурального числа n истины утверждения:
Теория вероятностей и математическая статистика Теория вероятностей Введение Предмет теории вероятностей. Наблюдаемые нами события (явления) можно подразделить на следующие три вида: достоверные, невозможные и случайные. Достоверным называют событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий S. Например, если в сосуде содержится вода при нормальном атмосферном давлении и температуре 20°, то событие «вода в сосуде находится в жидком состоянии» есть достоверное. В этом примере заданные атмосферное давление и температура воды составляют совокупность условий S. Невозможным называют событие, которое заведомо не произойдет, если будет осуществлена совокупность условий S. Например, событие «вода в сосуде находится в твердом состоянии» заведомо не произойдет, если будет осуществлена совокупность условий предыдущего примера. Случайным называют событие, которое при осуществлении совокупности условий 5 может либо произойти, либо не произойти. Например, если брошена монета, то она может упасть так, что сверху будет либо герб, либо надпись. Поэтому событие «при бросании монеты выпал «герб» - случайное. Каждое случайное событие, в частности выпадение «герба», есть следствие действия очень многих случайных причин (в нашем примере: сила, с которой брошена монета, форма монеты и многие другие). Невозможно учесть влияние на результат всех этих причин, поскольку число их очень велико и законы их действия неизвестны. Поэтому теория вероятностей не ставит перед собой задачу предсказать, произойдет единичное событие или нет, - она просто не в силах это сделать. По-иному обстоит дело, если рассматриваются случайные события, которые могут многократно наблюдаться при осуществлении одних и тех же условий S, т. е. если речь идет о массовых однородных случайных событиях. Оказывается, что достаточно большое число однородных случайных событий независимо от их конкретной природы подчиняется определенным закономерностям, а именно вероятностным закономерностям. Установлением этих закономерностей и занимается теория вероятностей. Итак, предметом теории вероятностей является изучение вероятностных закономерностей массовых однородных случайных событий. Знание закономерностей, которым подчиняются массовые случайные события, позволяет предвидеть, как эти события будут протекать. Например, хотя, как было уже сказано, нельзя наперед определить результат одного бросания монеты, но можно предсказать, причем с небольшой погрешностью, число появлений «герба», если монета будет брошена достаточно большое число раз. При этом предполагается, конечно, что монету бросают в одних и тех же условиях. Методы теории вероятностей широко применяются в различных отраслях естествознания и техники: в теории надежности, теории массового обслуживания, в теоретической физике, геодезии, астрономии, теории стрельбы, l теории ошибок наблюдений, теории автоматического управления, общей теории связи и во многих других теоретических и прикладных науках. Теория вероятностей служит также для обоснования математической и прикладной статистики, которая в свою очередь используется при планировании и организации производства, при анализе технологических процессов, предупредительном и приемочном контроле качества продукции и для многих других целей. В последние годы методы теории вероятностей все шире и шире проникают в различные области науки и техники, способствуя их прогрессу. Краткая историческая справка. Первые работы, в которых зарождались основные понятия теории вероятно стей, представляли собой попытки создания теории азартных игр (Кардано, Гюйгенс, Паскаль, Ферма и другие в XVI—XVII вв.). Следующий этап развития теории вероятностей связан с именем Якоба Бернулли (1654—1705). Доказанная им теорема, получившая впоследствии название «Закона больших чисел», была первым теоретическим обоснованием накопленных ранее фактов. Дальнейшими успехами теория вероятностей обязана Муавру, Лапласу, Гауссу, Пуассону и др. Новый, наиболее плодотворный период связан с именами П. Л. Чебышева (1821—1894) и его учеников А.А.Маркова (1856—1922) и А.М.Ляпунова (1857—1918). В этот период теория вероятностей становится стройной математической наукой. Ее последующее развитие обязано в первую очередь русским и советским математикам (С. Н. Бернштейн, В. И. Романовский, А. И. Колмогоров, А. Я. Хинчин, Б. В. Гнеденко, И. В. Смирнов и др.). В настоящее премя ведущая роль в создании новых ветвей теории вероятностей также принадлежит советским математикам. Комбинаторика – раздел математики, который посвящен решению задач выбора и расположения элементов некоторого (конечного) множества в соответствии с заданным правилом, а так же подсчету числа возможных конфигураций. Общие задачи пересчета связаны с выборкой некоторого числа элементов из заданного базисного множества Х, состоящего из n элементов (n-множества). Такие задачи полезно делить на типы в зависимости от того, как выбираются элементы: с повторением или без повторения, с учетом порядка выбора или без него. Пример 1. В мешке 2 типа конфет А и В. Ребенку разрешили взять 2. Сколькими способами он может взять конфеты. Возможны 4 различных уточнения. 1. Повторения возможны и порядок важен. АА, АВ, ВА, ВВ. 2. Нельзя брать одинаковые, но порядок важен: АВ, ВА. 3. Повторения возможны, но порядок не имеет значения: АА, АВ, ВВ. 4. Нельзя брать одинаковые и порядок не имеет значения: АВ. Чтобы различать на уровне терминологии тип конкретной задачи, введем несколько определений. Любое подмножество Y мощности k базисного n-множества – выборка объема k из n элементов или (n,k)-выборка. Выборка называется упорядоченной, если порядок следования элементов в ней задан, т.е. две выборки, различающиеся лишь порядком следования элементов, считаются разными. В противном случае выборка называется неупорядоченной (в примере 1, 2 - упорядоченные выборки, а 3,4 – нет). (n,k)-размещением без повторений называется упорядоченная (n,k)-выборка, в которой элементы не могут повторяться. (n,k)-размещением с повторениями называется упорядоченная (n,k)-выборка, в которой элементы могут повторяться. (n,k)-сочетанием без повторений называется неупорядоченная (n,k)-выборка, элементы которой не могут повторяться. (n,k)-сочетанием с повторениями называется неупорядоченная (n,k)–выборка, элементы которой могут повторяться. Число (n,k)-размещений без повторений обозначается 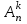 и определяется формулой: и определяется формулой:  . При n=kполучаем число возможных упорядочений n-множества (число перестановок): . При n=kполучаем число возможных упорядочений n-множества (число перестановок): 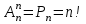 Число (n,k)-размещений с повторениями 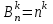 . .Число (n,k)-сочетаний без повторений обозначается 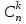 и определяется формулой: и определяется формулой: 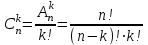 . .Число (n,k)-сочетаний с повторениями равно 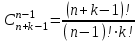 . .
Пример 2. Секрет замка. Всего 12 букв, секретное «слово» состоит из 5 букв. Число различных кодов замка 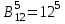 . .Пример 3. Найти число возможных распределений золотой, серебряной и бронзовых медалей в первенстве страны по футболу, если в нем участвует16 команд. 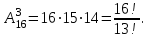 Пример 4. Сколькими способами можно разбить на подгруппы из 4 человек 16 участников шахматного первенства. 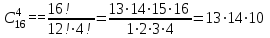 . .Пример 5. Сколько различных вариантов можно получить, бросая 5 игральных костей? Результат бросания 5 костей можно рассматривать как неупорядоченный набор 5 объектов (для каждого из которых есть 6 вариантов) с повторениями, т.е. это (6,5)-сочетание с повторениями. По общей формуле получаем общее число вариантов: 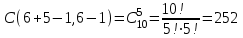 . .I. Предмет теории вероятностей и историческая справка. Теория вероятностей – это раздел математики, который изучает математические модели случайных явлений. Основой исследований в ТВ является наблюдение и опыт. Различают две основные характеристики опыта: случайное событие – качественная характеристика и случайная величина – количественная характеристика опыта. Случайное событие характеризуется тем, что исход опыта, в результате которого оно наблюдается, неоднозначен, так как зависит от многих факторов, каждый из которых отдельно не оказываете определяющего значения на результат. Случайная величина (функция, вектор и т.д.) принимает одно из своих возможных значений, до опыта неизвестно, какое именно. В ТВ рассматриваются (изучаются) массовые случайные события, которые возникают в результате осуществления условий, повторяющихся много раз. Теория вероятностей находит применение в различных разделах физики, в баллистике, лежит в основе математической и прикладной статистики. Теория вероятностей зародилась в середине 17 века, первоначально была связана с решением задач в азартных играх (поиск стратегии выигрыша). Успехи в развитии ТВ в это время связаны с именами следующих ученых: Паскаль, Ферма, Гюйгенс. Во второй половине 17 века Яков Бернулли, на основе обобщения результатов множества опытов формулирует статистическое определение вероятности. В 18 веке развитие ТВ связано с именами Муавра, Лапласа, Гаусса, Пуассона. А в 19 веке ведущее положение в ТВ занимает Российская (Петербургская) математическая школа: Чебышев, Марков, Ляпунов. Их приемниками в 20 веке стали российские математики: Хинчин, Бернштейн, Колмогоров, Гнеденко и др. II. Понятие частоты случайного события. Статистическое определение вероятности. Проведем опыт (эксперимент), который заключается в подбрасывании игрального кубика (кости). В результате мы можем наблюдать одно из возможных случайных событий: «выпало k очков» (k=1,2,3,4,5,6). Обозначим через А событие «выпало 6 очков». Проведем наш опыт n раз, через nA обозначим число опытов, в которых выпало 6 очков, т.е. произошло событие А. Частотой случайного события А называется число 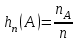 (1). Экспериментально было установлено (Я. Бернулли), что с увеличением числа опытов ( (1). Экспериментально было установлено (Я. Бернулли), что с увеличением числа опытов (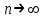 ) частота случайного события стремится к определенному числу ( ) частота случайного события стремится к определенному числу (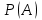 ), т.е. ), т.е. 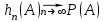 . Это свойство называется статистической устойчивостью частот. Массовые случайные события этим свойством обладают. Ясно, что число P(A) можно рассматривать, как объективную оценку возможности появления случайного события А. Сформулируем статистическое определение вероятности . Это свойство называется статистической устойчивостью частот. Массовые случайные события этим свойством обладают. Ясно, что число P(A) можно рассматривать, как объективную оценку возможности появления случайного события А. Сформулируем статистическое определение вероятностиОпределение 1.1. Конечное число P(A), к которому стремится частота события А при неограниченном увеличении числа опытов, называется вероятностью этого события, т.е. 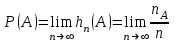 . (1.1) . (1.1)Это определение грешит тем, что для определения вероятности нужно найти частоту, т.е. произвести опыты. III. Пространство элементарных событий. Мы хотим построить математическую модель случайного явления. Для этого, прежде всего, нужно дать математическое описание опыта, для исходов которого мы собираемся вычислять вероятность.Предварительно рассмотрим несколько примеров. Пример 6. Опыт заключается в том, что один раз выбрасывают игральную кость. В результате возникают различные случайные события, например, выпало 1очко, выпало 3 очка, выпало 6 очков, выпало четное число очков и т.д. Первые три события неразложимы на более простые события, их принято называть элементарными событиями. Последнее событие происходит в том случае, если выпало или 2, или 4, или 6 очков, т.е. оно не является элементарным. Обозначим через 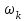 событие «выпало k очков». Тогда все элементарные события, которые могут наступить в нашем опыте, можно представить как множество событие «выпало k очков». Тогда все элементарные события, которые могут наступить в нашем опыте, можно представить как множество 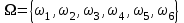 . Любое составное событие можно интерпретировать как подмножество . Любое составное событие можно интерпретировать как подмножество 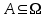 . Например, событие «выпало четное число очков» – это подмножество . Например, событие «выпало четное число очков» – это подмножество 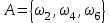 . С другой стороны, любое подмножество . С другой стороны, любое подмножество 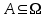 ( в частности и ( в частности и 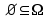 , например, , например, 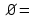 {выпало более 6 очков}) можно считать случайным событием, произошедшим в результате данного опыта. Таким образом, задав множество {выпало более 6 очков}) можно считать случайным событием, произошедшим в результате данного опыта. Таким образом, задав множество 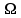 , мы описали данный опыт, построили его модель. Множество , мы описали данный опыт, построили его модель. Множество 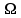 принято называть пространством элементарных событий. принято называть пространством элементарных событий.Пример 7. Опыт заключается в том, что три раза подбрасывают монету и фиксируют сторону, на которую она упала: герб отмечают 1, а решку – 0. Результат любого опыта – это упорядоченная тройка, каждый элемент которой либо 0, либо 1. Перебирая все возможности построения таких троек, получим множество всех элементарных событий в этом опыте – конечное множество  . Любое случайное событие можно отождествить с подмножеством множества . Любое случайное событие можно отождествить с подмножеством множества 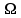 . Например, событие А={герб выпал на 1–м броске} это подмножество . Например, событие А={герб выпал на 1–м броске} это подмножество 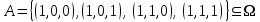 . И наоборот, любое подмножество . И наоборот, любое подмножество 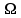 можно описать, как некоторое случайное событие, наступившее в этом опыте. Например, можно описать, как некоторое случайное событие, наступившее в этом опыте. Например, 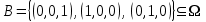 – «в результате опыта решка появилась точно два раза». – «в результате опыта решка появилась точно два раза».Пример 8. Опыт заключается в выстреле по неограниченной плоской мишени. Наблюдаемый результат (элементарное событие) точка на мишени (на плоскости), т.е. элементарное событие – 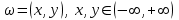 , а пространство элементарных событий – это множество всех точек плоскости, на которой введена декартова система координат. Любое подмножество является случайным событием, и любое событие можно представить как некоторое подмножество. Например, , а пространство элементарных событий – это множество всех точек плоскости, на которой введена декартова система координат. Любое подмножество является случайным событием, и любое событие можно представить как некоторое подмножество. Например, 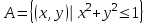 можно рассматривать как «попадание в десяточку». можно рассматривать как «попадание в десяточку».Анализируя эти примеры, видим, что для описания опыта нужно ввести в рассмотрение все его мыслимые простейшие исходы – множество всех элементарных событий. Тогда любое событие – это некоторое подмножество данного множества. Определение 1.2. Пространством элементарных событий называется произвольное множество 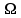 , а любой его элемент называется элементарным событием. , а любой его элемент называется элементарным событием.Отметим, что для описания реального опыта пространство элементарных событий выбирают подходящим образом, причем, выбор зависит и от того, какие события нас интересуют в данной задаче. IV. Алгебра событий. Если множество 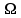 – пространство элементарных событий, то любое случайное событие является его подмножеством. В случае, когда – пространство элементарных событий, то любое случайное событие является его подмножеством. В случае, когда 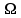 конечное или счетное множество любое подмножество – это событие. Но если конечное или счетное множество любое подмножество – это событие. Но если 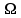 – несчетное множество, случайными событиями являются не все подмножества, а только определенный класс подмножеств, который будет введен после определения операций над событиями. Событие – несчетное множество, случайными событиями являются не все подмножества, а только определенный класс подмножеств, который будет введен после определения операций над событиями. Событие 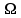 – достоверное событие, а событие – достоверное событие, а событие 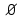 – невозможное событие. – невозможное событие. Сумма событий. 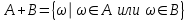 . Пример. Диаграмма. . Пример. Диаграмма.Произведение событий. 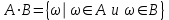 . Пример. Диаграмма. . Пример. Диаграмма.Разность событий. 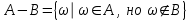 . Пример. Диаграмма. . Пример. Диаграмма.Противоположное событие. 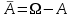 , т.е. событие А не происходит. Пример. Диаграмма. , т.е. событие А не происходит. Пример. Диаграмма.События А и В называются несовместными, если 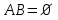 . Если . Если 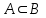 ,то наступление события А влечет за собой событие В. События А и В называются равными или равносильными (А=В), если ,то наступление события А влечет за собой событие В. События А и В называются равными или равносильными (А=В), если 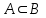 и и 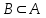 . .Определение суммы и произведения событий переносится на бесконечную последовательность событий: 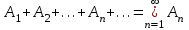 , , 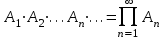 . .Свойства операций над событиями – это фактически свойства операций над множествами, т.к. 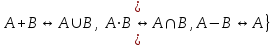 а противоположное событие соответствует операции дополнения. а противоположное событие соответствует операции дополнения.Определение 1.3. Класс 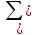 подмножеств пространства элементарных событий подмножеств пространства элементарных событий 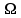 называется алгеброй событий, если 1) называется алгеброй событий, если 1) 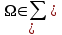 , 2) , 2) 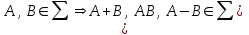 (класс замкнут относительно операций). Если замкнут относительно бесконечных сумм и произведений, то класс называется (класс замкнут относительно операций). Если замкнут относительно бесконечных сумм и произведений, то класс называется 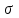 –алгеброй (сигма–алгеброй). –алгеброй (сигма–алгеброй).V. Определение вероятности и вероятностного пространства. Не существует определения вероятности, по которому можно найти числовое значение вероятности события в любой задаче. В качестве общего определения используют аксиоматическое определение (система аксиом определяется неоднозначно). Выделяются условия, которым должна удовлетворять любая функция, претендующая на роль вероятностной функции. Эти условия являются не чем иным, как обобщенными (характеристическими) свойствами частоты события. Определение 1.4 (аксиоматическое определение вероятности). Числовая функция Р=Р(А), определенная на алгебре событий 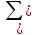 ( (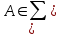 ) называется вероятностью, если выполняются следующие аксиомы: ) называется вероятностью, если выполняются следующие аксиомы:А1. 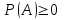 для для 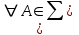 (аксиома неотрицательности). (аксиома неотрицательности).А2. 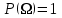 (аксиома нормированности). (аксиома нормированности).А3. 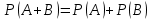 для любых несовместных событий для любых несовместных событий 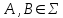 (аксиома аддитивности). (аксиома аддитивности).В некоторых случаях добавляют аксиому расширенной аддитивности. А4. 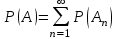 , если , если 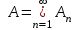 , ,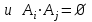 . .Определение 1.5. Тройка 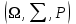 , где , где 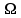 – пространство элементарных событий, – пространство элементарных событий, 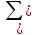 – алгебра событий и Р – вероятностная функция, удовлетворяющая аксиомам А1–А3 (А1–А4) называется вероятностным пространством. – алгебра событий и Р – вероятностная функция, удовлетворяющая аксиомам А1–А3 (А1–А4) называется вероятностным пространством.Вероятностное пространство – это самая общая модель случайного явления. Математическая статистика ВЫБОРОЧНЫЙ МЕТОД | ||||||||||||||||||||||||||

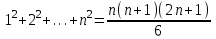 ;
;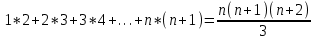 ;
;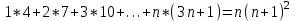 ;
;