производные. Тема производная и дифференциал

• Название: Тема производная и дифференциал
• Анкор: ....
• Дата: 14.09.2021
• Размер: 1.39 Mb.
• Имя файла: производные.doc
• Тип: Решение; #232184
• страница: 1 из 5

Производная и дифференциал

ТЕМА 5. Производная и дифференциал
1. Производная.

2. Дифференциал.

3. Производные и дифференциалы высших порядков.

4. Свойства дифференцируемых функций.

Решение типового варианта
Пример 1.

Найти производные заданных функций
а) ;

Решение:

;

.
б) ;

Решение:

Используем формулу .

.
в) ;

Решение:

Используем формулу .

.
г) ;

Решение:

Используем формулу .

, где ;

.
д) ;

Решение:

Используем формулу .

, где ;

.
е) ;

Решение:


Пример 2.

Найти :
а) .

Решение:

Функция в примере задана неявно. Чтобы найти ее производную продифференцируем обе части равенства по x, полагая, что у есть функция от х и обозначая производную у через :

.

Выразим из полученного равенства :

;

.
б) .

Решение:

Аналогично предыдущему примеру:

;

;

.
в)

Решение:

Используем формулу .

.
Пример 3.

Найти :
а) ;

Решение:

;



б) .

Решение:




Пример 4.

Найти дифференциал функции , если .
Решение:

Воспользуемся свойством логарифма частного для упрощения формулы:

.

Используем формулу .

;


Пример 5.

Составить уравнения касательной и нормали к кривой в точке с абсциссой .
Решение:

Найдем ординату точки касания:

.

Угловой коэффициент касательной равен значению производной в точке :

.

Подставляем значения и в уравнение касательной :

,

получили уравнение касательной .

Подставляем значения и в уравнение нормали :

,

получили уравнение нормали .

Вариант 1
1. Найти производные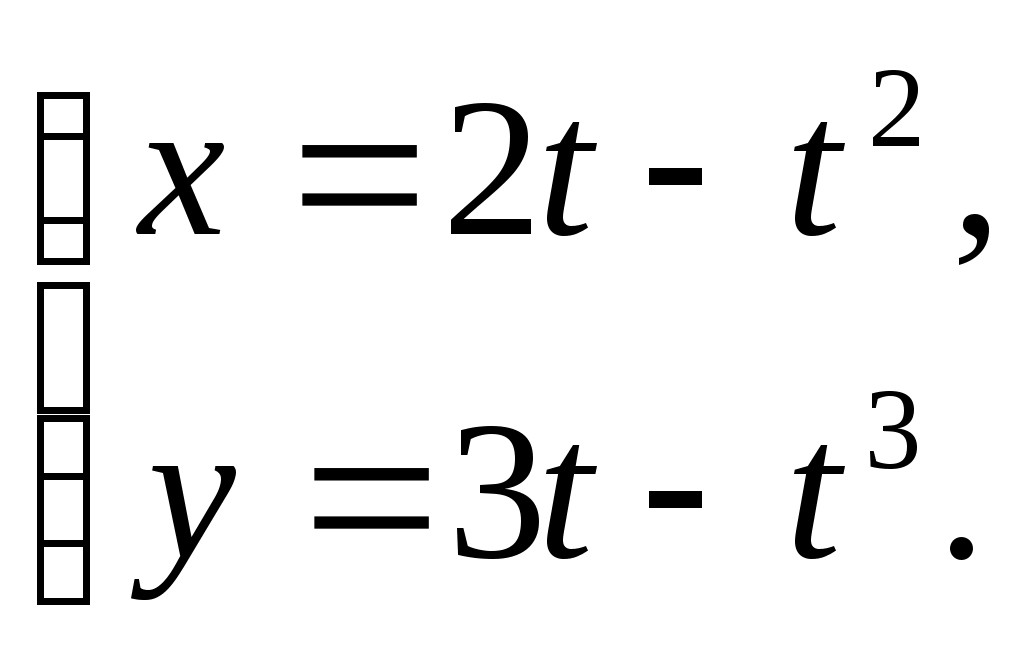

1. 
   ,
   
2. 
   ,
   
3. 
   ,
   
4. 
   ,
   
5. 
   ,
   
6. 
   ,
   
7. 
   ,
   
8. 
   ,
   
9. 
   ,
   
10. 
    ,
    
11. 
    ,
    
12. 
    .
    

2. Найти :

1. 
   ,
   
2. 
   ,
   
3. 
   
   

3. Найти :



4. Найти дифференциал функции:



5. Составить уравнения касательной и нормали к линии в точке с абсциссой .
Вариант 2

1. Найти производные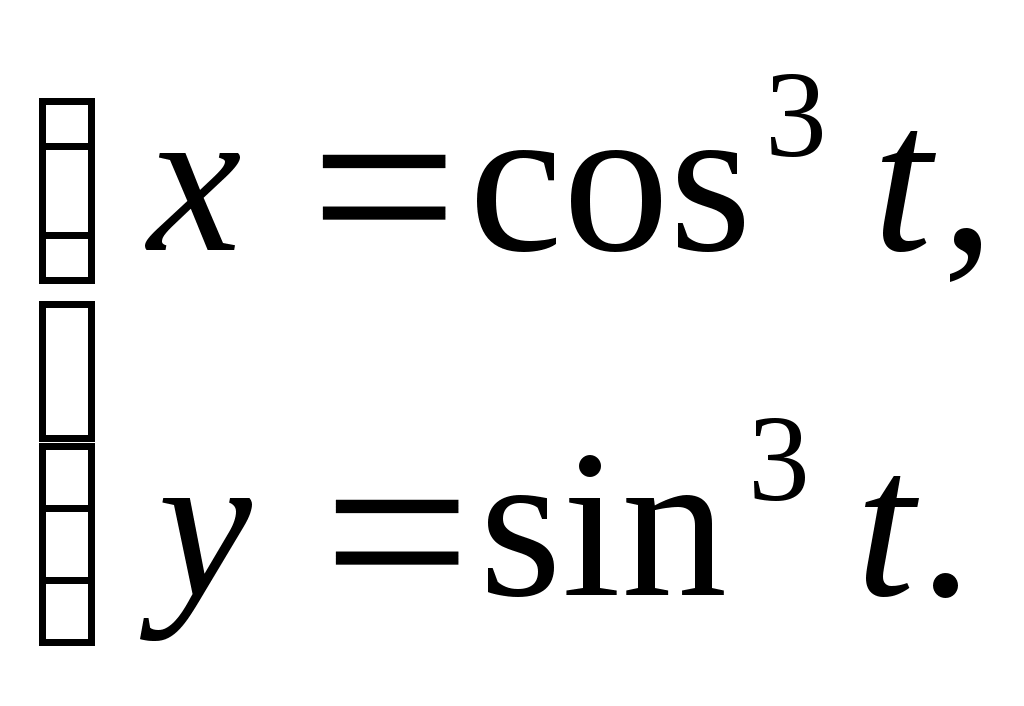

1. 
   ,
   
2. 
   ,
   
3. 
   ,
   
4. 
   ,
   
5. 
   ,
   
6. 
   ,
   
7. 
   ,
   
8. 
   ,
   
9. 
   ,
   
10. 
    ,
    
11. 
    ,
    
12. 
    ,
    

2. Найти :

1. 
   ,
   
2. 
   ,
   
3. 
   
   

3. Найти :



4. Найти дифференциал функции:



5. Составить уравнения касательной и нормали к линии в точке с абсциссой .
Вариант 3

1. Найти производные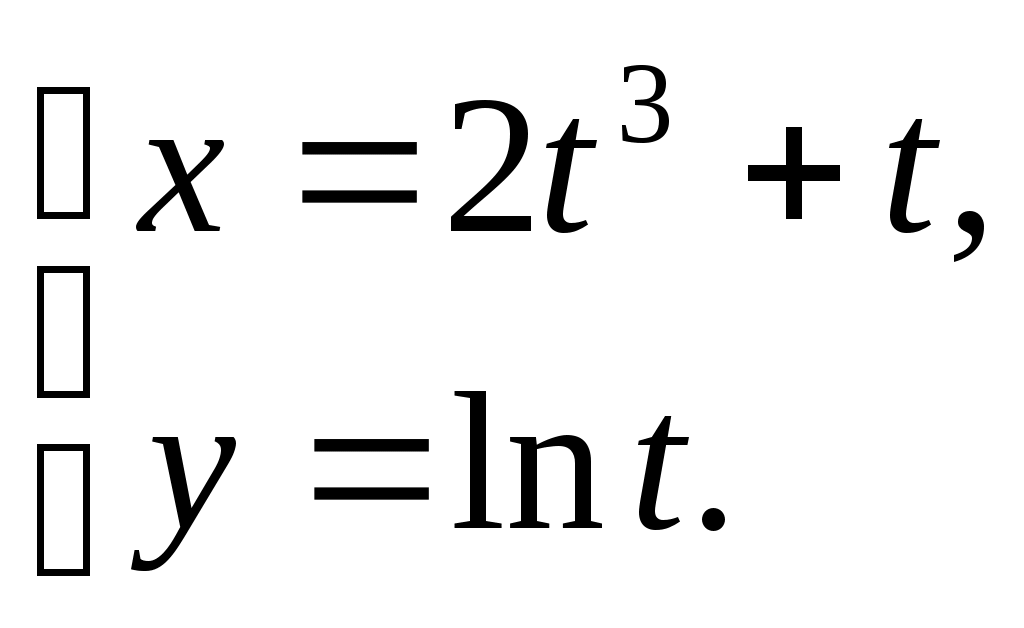

1. 
   ,
   
2. 
   ,
   
3. 
   ,
   
4. 
   ,
   
5. 
   ,
   
6. 
   ,
   
7. 
   ,
   
8. 
   ,
   
9. 
   ,
   
10. 
    ,
    
11. 
    ,
    
12. 
    .
    

2. Найти :

1. 
   ,
   
2. 
   ,
   
3. 
   
   

3. Найти :



4. Найти дифференциал функции:



5. Составить уравнения касательной и нормали к линии в точке с абсциссой .

Вариант 4

1. Найти производные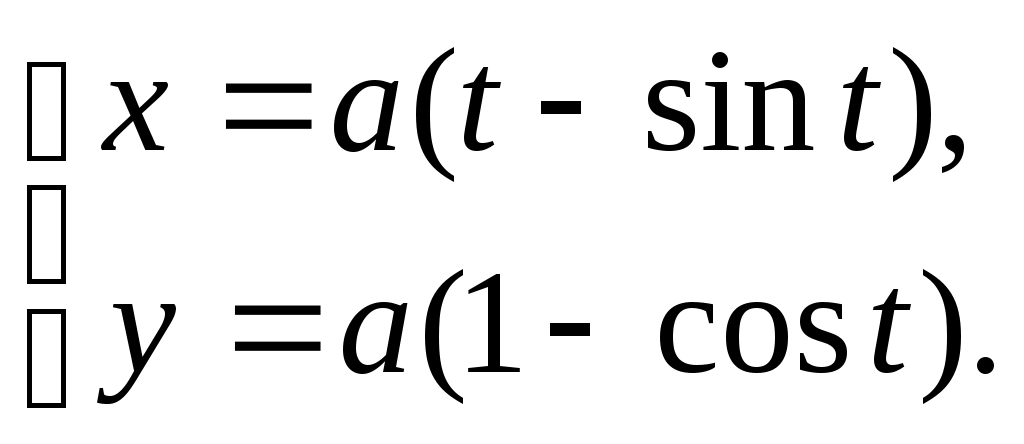

1. 
   ,
   
2. 
   ,
   
3. 
   ,
   
4. 
   ,
   
5. 
   ,
   
6. 
   ,
   
7. 
   ,
   
8. 
   ,
   
9. 
   ,
   
10. 
    ,
    
11. 
    ,
    
12. 
    .
    

2. Найти :

1. 
   ,
   
2. 
   ,
   
3. 
   
   

3. Найти :



4. Найти дифференциал функции:



5. Составить уравнения касательной и нормали к линии в точке с абсциссой .