Тема Технология получения статистических показателей (основные теоретические положения)
 Скачать 194.84 Kb. Скачать 194.84 Kb.
|
1.3. Абсолютные и относительные показателиПод статистическим показателем понимают обобщающую количественную характеристику какого-то свойства (признака) группы единиц или совокупности в целом. По форме выражения статистические показатели подразделяются на абсолютные, относительные и средние показатели или величины. Абсолютные показатели являются первичной формой выражения статистических показателей и получаются в результате сводки. Они характеризуют абсолютные размеры изучаемых явлений и процессов (массу, площадь, объем, протяженность и т. д.), отражают их временные характеристики, а также могут представлять объем совокупности, т. е. число составляющих ее единиц. Абсолютные показатели всегда имеют размерность, т. е. являются именованными числами. В зависимости от сущности изучаемых явлений, их физических свойств, они выражаются в натуральных, трудовых или стоимостных единицах измерения. Под натуральными понимают физические единицы измерения величин (тонны, килограммы, метры простые, квадратные и кубические, мили, литры, баррели, штуки и т. д.). В группу натуральных входят также условно-натуральные измерители, которые используются в тех случаях, когда какой-либо продукт имеет несколько разновидностей и общий объем можно определить исходя из общего для всех разновидностей свойства. Например, различные виды органического топлива переводят в условное топливо с теплотой сгорания 29,3 мДж/кг (7000 ккал/кг), мыло разных сортов – в условное мыло с 40%-ным содержанием кислот, консервы различного объема – в условные консервные банки объемом 353,4 см3 и т. д. Перевод в условные единицы измерения осуществляется на основе коэффициентов, рассчитываемых как отношение значений, характеризующих взятое за основу свойство по разновидностям продукции, к эталонному значению. Например, предприятие в отчетном периоде выпустило 10 т мыла 40%-ной , 20 т – 68%-ной и 30 т – 72%-ной жирности. Если в качестве эталона взять 1 т мыла 40%-ной жирности, то можно говорить о том, что выпуск 1 т мыла 68%-ной жирности адекватен выпуску 1,7 т мыла 40%-ной жирности (68/40), а выпуск 1 т мыла 72%-ной жирности эквивалентен выпуску 1,8 т мыла 40%-ной жирности. Общий выпуск продукции предприятием составил 98 т условного мыла 40%-ной жирности (10+20·1,7+30·1,8). Трудовые единицы измерения позволяют учитывать затраты рабочего времени на предприятиях, а также трудоемкость отдельных операций технологического процесса. К ним относятся человеко-дни и человеко-часы. Стоимостные единицы измерения основаны на использовании цен и позволяют получать обобщающие денежные оценки социально-экономических процессов и явлений. Стоимостные единицы измерения являются наиболее универсальными. Для того, чтобы сделать полный анализ исследуемых явлений, выявить их взаимосвязи и установить закономерности развития, абсолютных показателей недостаточно. При сравнении и сопоставлении социально-экономических явлений используются относительные показатели. Относительный показатель представляет собой результат деления одного абсолютного показателя на другой и выражает соотношение между количественными характеристиками социально-экономических явлений и процессов. При расчете относительных показателей абсолютный показатель, находящийся в числителе соотношения, называется текущим или сравниваемым. Показатель, с которым производится сравнение и который находится в знаменателе, называется основанием или базой сравнения. Относительный показатель указывает, во сколько раз сравниваемый показатель больше базисного либо какую он составляет от него долю, либо сколько единиц первого приходится на 1, 100, 1000, 10 000 и т. д. единиц знаменателя. Относительные показатели могут выражаться в коэффициентах, процентах, промилле, продецимилле или быть именованными числами. По сущности и назначению выражаемых количественных соотношений различают следующие виды относительных величин: планового задания, выполнения плана, динамики, сравнения, структуры, координации, интенсивности. Относительная величина планового задания (ОВПЗ) – отношение планового задания текущего (отчетного) периода к фактическому значению показателя в предыдущем периоде. Например, в 2015 г. предприятие выпустило продукции на 200 млрд. руб., в 2016 г. запланирован выпуск продукции на 240 млрд. руб. ОВПЗ = план отчетного периода / факт предыдущего периода = = 240 / 200=1,20 (120%). Плановое задание составляет 120% от факта предыдущего периода, или на 20% превосходит выпуск предыдущего периода. Относительная величина выполнения планового задания (ОВВП) – отношение фактического значения к плановому заданию по нему за один и тот же период. Например, по плану на 2016 г. предприятие должно было выпустить продукции на 240 млрд. руб., а фактически выпустило продукции на 252 млрд. руб. ОВВП = факт отчетного периода / план отчетного периода = = 252 / 240 = 1,05 (или 105%). Выполнение плана по выпуску продукции составило 105%,т. е. план перевыполнен на 5%. Относительная величина динамики (ОВД) характеризует изменение явления во времени и представляет собой соотношение значений одного и того же показателя за различные периоды времени. Например, в 2015 г. выпуск продукции на предприятии составил 200 млрд. руб., а в 2016 г. – 252 млрд. руб. ОВД = факт отчетного года / факт предыдущего года = = 252 / 200 =1,26 (126%). Выпуск продукции предприятия в 2016 г. составил 126% от выпуска предыдущего года, т. е. предприятием выпущено продукции на 26% больше. Относительные величины динамики за ряд лет могут быть исчислены по отношению как к предыдущему периоду, так и к одному и тому же базисному году (например, к 2000 г.). В первом случае они называются цепными, во втором – базисными. Относительные величины динамики, планового задания и выполнения планового задания находятся во взаимосвязи – произведение относительных величин выполнения плана и планового задания равно относительной величине динамики. ОВД = ОВПЗ ОВВП = 1,20 1,05 = 1,26. Относительная величина сравнения (ОВСр) – отношение одного и того же показателя за один и тот же момент времени, но по различным территориям или объектам. Например, численность работников предприятия А – 300 чел., а предприятия Б – 200 чел. ОВСр = значение показателя по объекту А / / значение показателя по объекту Б = = 300 / 200 = 1,5 (150%). Численность работников предприятия А составляет 150% от численности работников предприятия Б, или численность работников предприятия А в 1,5 раза больше, чем предприятия Б. Относительная величина структуры (ОВСт) характеризует состав изучаемой совокупности и представляет собой отношение части целого к целому. Например, на предприятии с общей численностью работников 300 чел. трудятся 90 женщин. ОВСт= часть целого / целое = 90 / 300 = 0,3 (30%). Доля (удельный вес) женщин в общей численности работников предприятия составляет 30%. Относительная величина координации (ОВК) характеризует пропорции между отдельными частями совокупности и представляет собой отношение отдельных частей целого друг к другу. Например, на предприятии работает 210 мужчин и 90 женщин. ОВК = часть целого / часть целого = 210 / 90 = 2,2. На предприятии работает в 2,2 раза больше мужчин, чем женщин. Относительная величина интенсивности (ОВИ) характеризует степень распространения явления в определенной среде или по отношению к другому показателю. В отличие от всех других относительных величин, это единственная именованная величина, поскольку она представляет собой результат сопоставления разноименных величин и характеризует итог числителя, приходящийся на 1, 10, 100, 1000 и т. д. единиц знаменателя. Пример. В одном из районов города, где проживает 200 тыс. чел., в отчетном периоде зарегистрировано 80 браков. ОВИ = 80 / 200 000 = 4 / 10 000 брака/чел. Уровень брачности в этом районе города составляет 4 брака на 10 000 человек. Средняя арифметическая величина Наиболее распространенной формой статистического показателя является средняя величина. В статистике применяют различные виды средних величин: степенные средние (арифметическая, гармоническая, геометрическая, квадратическая, кубическая и т.д.), средняя хронологическая, а также структурные средние (мода и медиана). Однако наиболее часто в социально-экономических исследованиях используется средняя арифметическая величина, которая отражает типичный уровень признака в совокупности. Ее широкое применение объясняется тем, что она позволяют сравнивать значения признака у единиц, относящихся к разным совокупностям. Например, можно сравнивать среднюю продолжительность рабочего дня, средний тарифный разряд рабочих, средний уровень заработной платы по различным предприятиям. Сущность средней арифметической заключается в том, что в ней взаимопогашаются отклонения значений признака у отдельных единиц совокупности, обусловленные действием случайных факторов. Поэтому средняя арифметическая величина должна рассчитываться для достаточно многочисленных совокупностей (действует закон больших чисел). Ее надежность зависит также от колеблемости значений признака в совокупности. В общем случае, чем меньше вариация признака и чем больше совокупность, по которой определяется средняя арифметическая величина, тем она надежнее. Типичность средней арифметической величины непосредственным образом связана также с однородностью статистической совокупности. Она только тогда будет отражать типичный уровень признака, когда рассчитана по однородной совокупности. В противном случае метод средних используется в сочетании с методом группировок: общие средние заменяются или дополняются групповыми средними, рассчитанными по однородным группам. Средняя арифметическая величина применяется в форме простой средней и взвешенной средней. Средняя арифметическая простая рассчитывается по несгруппированным данным на основании формулы 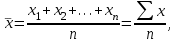 где х – индивидуальные значения признака; n – число единиц в статистической совокупности. Пример. Требуется найти среднюю выработку рабочего в бригаде, состоящей из 15 человек, если известно количество изделий (штук), произведенных одним рабочим в смену: 21; 20; 20; 19; 21; 19; 18; 22; 19; 20; 21; 20; 18; 19; 20. 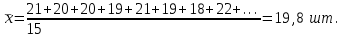 Таким образом, сменная выработка одного рабочего бригады в среднем составляет 19,88 тук. Средняя арифметическая взвешенная рассчитывается по сгруппированным данным: 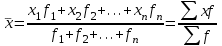 , ,где f – частота повторения соответствующего варианта значения признака в статистической совокупности. Пример. На основании имеющихся данных о распределении рабочих бригады по количеству выработанных ими изделий (гр.1 и гр. 2) требуется найти среднюю выработку рабочего в бригаде.
Решение. Для упрощения расчетов таблица дополнена графой 3, суммарный итог по которой подставлен в формулу: 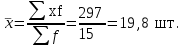 Поскольку в задаче использованы исходные данные предыдущей задачи, но в сгруппированном виде, то результаты расчетов совпадают – сменная выработка одного рабочего бригады в среднем составляет 20 штук. Средняя величина признака в совокупности может рассчитываться на базе как индивидуальных значений признака, так и групповых (частных) средних, исчисленных по отдельным частям совокупности. При этом используется формула средней арифметической взвешенной, где в качестве вариантов значений признака рассматриваются групповые (частные) средние ( 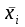 ). ).Пример. Имеются данные о среднем стаже рабочих по цехам завода (гр.1 и гр. 2). Требуется определить средний стаж рабочих в целом по заводу.
Решение. Для упрощения расчетов таблица дополнена графой 3, суммарный итог по которой подставлен в формулу: Р 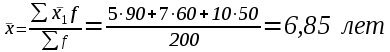 асчеты показывают, что средний стаж рабочих в целом по заводу составляет 6,85 лет. В случае, когда значения осредняемого признака заданы в виде интервалов, при расчете средней арифметической величины используются средние значения признака в интервалах (x´). При этом величина открытых интервалов (как правило, это первый и последний), условно приравнивается к величине интервалов, примыкающих к ним. Пример. Имеются данные о распределении рабочих предприятия по уровню заработной платы (гр.1 и гр. 2). Требуется определить среднюю заработную плату рабочих предприятия.
Решение. Для упрощения расчетов таблица дополнена графой 3, где указано среднее значение заработной платы в каждом интервале, а также графой 4 с промежуточными расчетами. Суммарный итог по графе 4 подставлен в формулу: 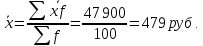 Расчеты показывают, что средняя заработная плата рабочих завода составляет 479 руб. Показатели вариации признака Зарегистрированные в процессе статистического наблюдения различия величины признака у отдельных единиц совокупности называются вариацией признака. По степени вариации признака можно судить о процессах развития изучаемых явлений, о типичности средних величин. Дело в том, что средняя величина дает обобщающую характеристику признака изучаемой совокупности, но она не раскрывает строения совокупности. Она не показывает, как относительно нее располагаются варианты осредняемого признака – сосредоточены ли они вблизи средней или значительно отклоняются от нее. Средняя величина признака в двух совокупностях может быть одинаковой, но в одном случае все индивидуальные значения могут мало отличаться от нее, а в другом – эти отличия могут быть велики, т. е. в одном случае вариация признака мала, а в другом – велика, что имеет большое значение для характеристики надежности средней величины. Для определения меры вариации признака в статистике используются абсолютные и относительные показатели вариации. К абсолютным показателям вариации относятся: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение. Размах вариации (R) является самым простым из абсолютных показателей вариации и представляет собой разность между максимальным и минимальным значениями признака: |
