Тема Технология получения статистических показателей (основные теоретические положения)
 Скачать 194.84 Kb. Скачать 194.84 Kb.
|
R = Xmax – Xmin ,где Xmax и Xmin – максимальное и минимальное значение признака в статистической совокупности;Величина размаха вариации зависит только от крайних значений и не учитывает всех изменений признака в пределах изучаемой совокупности. Поэтому при изучении вариации нельзя ограничиваться расчетом только этого показателя. Для анализа вариации необходимы показатели, дающие обобщенную характеристику всех колебаний варьирующего признака. Среднее линейное отклонение – простейший обобщающий показатель. Он представляет собой среднюю величину абсолютных отклонений индивидуальных значений признака от их средней арифметической величины. Среднее линейное отклонение для несгруппированных данных определяется по формуле 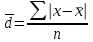 . .Среднее линейное отклонение для сгруппированных данных рассчитывается так: 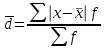 . .Среднее линейное отклонение не всегда улавливает степень вариации значений признака. Поэтому в статистике применяется более чувствительный обобщающий показатель – дисперсия, которая представляет собой средний квадрат отклонений индивидуальных значений признака от их средней арифметической величины. Дисперсия для несгруппированных данных вычисляется по формуле 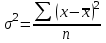 . .Дисперсия для сгруппированных данных рассчитывается так: 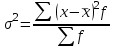 . .Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии: 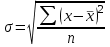 , ,или 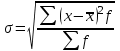 . .Среднее квадратическое отклонение также, как и среднее линейное отклонение показывает, на сколько в среднем отличаются индивидуальные значения признака от их среднего значения. Однако по величине среднеквадратическое отклонение во всех случаях превышает среднее линейное, так как более чутко реагирует на вариацию. Для симметричных и умеренно асимметричных распределений имеет место следующее соотношение: 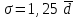 . .Размах вариации, средние линейное и квадратическое отклонения выражаются именованными числами, т. е. имеют единицу измерения (такую же, как и значения признака). Поэтому их нельзя непосредственно использовать для сравнения степени вариации по одному и тому же признаку в двух группах с разным уровнем средних, а также для сравнения вариации двух различных признаков в одной группе. В этих случаях применяются следующие относительные показатели вариации. Коэффициент осцилляции: 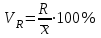 . .Относительное линейное отклонение (линейный коэффициент вариации). 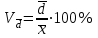 . .Коэффициент вариации.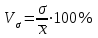 . .Коэффициент вариации позволяет не только получить обобщающую характеристику вариации признака в совокупности, но и дает возможность сделать выводы об однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33%. Средние величины, рассчитанные по однородной совокупности. Пример. Имеются данные о распределении рабочих организации по тарифному разряду (гр. 1, гр. 2). Требуется определить средний тарифный разряд рабочих, рассчитать абсолютные и относительные показатели вариации и сделать выводы о типичности средней величины для изучаемой совокупности.
Решение. Средний тарифный разряд рассчитаем по формуле средней арифметической взвешенной, поскольку исходные данные сгруппированы: 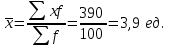 Для расчета показателей вариации выполним промежуточные вычисления в таблице (гр. 3–гр.7), учитывая что исходные данные сгруппированы. Определяем абсолютные показатели вариации: – размах вариации: 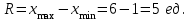 – среднее линейное отклонение: 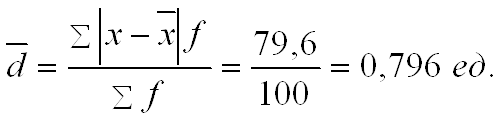 – дисперсия: 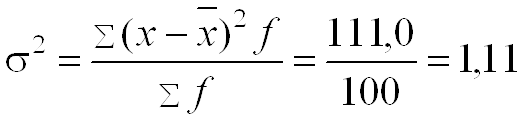 – среднее квадратическое отклонение: 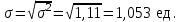 Определяем относительные показатели вариации: – коэффициент осцилляции: 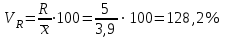 – относительное линейное отклонение: 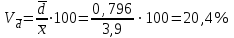 – коэффициент вариации: 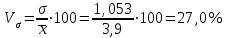 Таким образом, средний тарифный разряд (3,9) является типичным для этой совокупности рабочих, которая является однородной, о чем свидетельствует расчетное значение коэффициента вариации (27%), не превышающее 33%. 1.6. Показатели структуры распределения признака Помимо средней арифметической величины в статистике используются структурные средние величины, характеризующие распределение признака в совокупности. К ним относятся мода и медиана. Модой (Мо) называется значение изучаемого признака (вариант), которое чаще всего встречается в совокупности. В дискретном ряду мода определяется достаточно просто – по максимальному показателю частоты. В интервальном вариационном ряду мода приблизительно соответствует центру модального интервала, т. е. интервала, имеющего большую частоту (частость). Конкретное значение моды рассчитывается по формуле 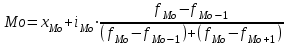 , ,где хMo – нижняя граница модального интервала; iMo– ширина модального интервала; fMo – частота, соответствующая модальному интервалу; fMo–1 – частота интервала, предшествующего модальному; fMo+1 – частота интервала, следующего за модальным. Медианой (Ме) называется значение признака, расположенное в середине ранжированного ряда (упорядоченного в порядке возрастания или убывания значений признака). Медиана делит ранжированный ряд на две части, одна из которых имеет значения признака не большие, чем медиана, а другая – не меньшие. Для ранжированного ряда с нечетным числом членов медианой является вариант, расположенный в центре ряда. Положение медианы определяется порядковым номером единицы ряда в соответствии с формулой 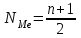 , (4.13) , (4.13)где n – число членов ранжированного ряда. Для ранжированного ряда с четным числом членов медианой является среднее арифметическое из двух смежных значений, находящихся в центре ряда. В интервальном вариационном ряду для нахождения медианы применяется следующая формула: 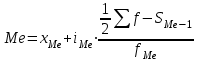 , (4.14) , (4.14)где xMе – нижняя граница медианного интервала; iMе – ширина медианного интервала; SMе-1 – накопленная частота интервала, предшествующего медианному; fMе – частота медианного интервала. Пример 1. Рабочие бригады, состоящей из 9 чел., имеют следующие тарифные разряды: 4; 3; 4; 5; 3; 3; 6; 2; 6. Требуется определить модальное и медианное значения тарифного разряда. Решение. Поскольку в данной бригаде больше всего рабочих 3-го разряда, то этот разряд и будет модальным (Мо=3), т. е. в бригаде чаще всего встречается пятый разряд. Для определения медианы осуществим ранжирование исходного ряда в порядке возрастания значений признака: 2; 3; 3; 3; 4; 4; 5; 6; 6. Центральным в этом ряду является пятое по счету значение признака. Соответственно Ме=4, т.е. половина рабочих имеет разряд не больше, чем четвертый, вторая – не меньше. Пример 2. Требуется определить модальный и медианный тарифный разряд рабочих завода по данным следующего ряда распределения.
Решение. Поскольку исходный ряд распределения является дискретным, то модальное значение определяется по максимальному показателю частоты. В данном примере на заводе больше всего рабочих 3-го разряда (fмах=30), т. е. этот разряд и является модальным (Мо=3). Определим положение медианы. Исходный ряд распределения построен на основании ранжированного ряда, упорядоченного по возрастанию значений признака. Середина ряда находится между 50-м и 51-м порядковыми номерами значений признака. Выясним, к какой группе относятся рабочие с этими порядковыми номерами. Для этого рассчитаем накопленные частоты. Накопленные частоты указывают на то, что третий разряд является медианным (Ме=3), поскольку значения признака с порядковыми номерами от 39-го до 68-го, в том числе 50-е и 51-е, равны 3. Пример 3. Требуется определить модальную и медианную заработную плату рабочих завода по данным следующего ряда распределения.
Решение. Поскольку исходный ряд распределения является интервальным, то модальное значение заработной платы рассчитывается по формуле. При этом модальным является интервал 360–420 с максимальной частотой, равной 30. М 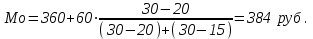 едианное значение заработной платы также рассчитывается по формуле. При этом медианным является интервал 360–420, накопленная частота которого равна 70, тогда как накопленная частота предыдущего интервала составляла только 40 при общем числе единиц, равном 100. Т 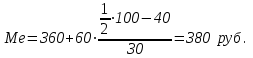 аким образом, модальная и медианная заработная плата составляют 384 руб. и 380 руб. соответственно. Помимо структурных средних более глубоко охарактеризовать изучаемую совокупность можно с помощью квартилей, децилей и перцентилей. Определяются они по аналогии с медианой и делят ранжированный ряд соответственно на 4, 10, 100 равных частей. Квартили представляют собой значения признака, разделяющие ранжированный ряд на четыре равновеликие части. Для расчета квартилей по интервальному ряду используются формулы: 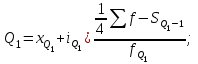 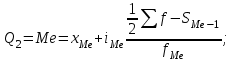 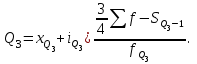 где хQ1 – нижняя граница интервала, содержащего нижний квартиль (накопленная частотам этого интервала превышает 25%); хQ2 – нижняя граница интервала, содержащего средний квартиль (накопленная частотам этого интервала превышает 50%); хQ3 – нижняя граница интервала, содержащего верхний квартиль (накопленная частотам этого интервала превышает 75%); iQ1, iQ2 и iQ3 – ширина интервала, содержащего нижний, средний и верхний квартиль соответственно; SQ1-1 , SQ2-1 , SQ3-1 – накопленная частота интервала, предшествующего интервалу, содержащему нижний, средний и верхний квартиль соответственно; fQ1, fQ2, fQ3 – частота интервала, содержащего нижний, средний и верхний квартиль соответственно. Децили – значения признака, разделяющие ранжированную совокупность на десять равных частей. Вычисляются по той же схеме, что и квартили: 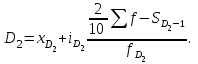 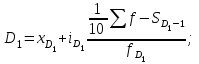 Перцентили – это значения признака, разделяющие ранжированный ряд на 100 равных частей. Определяются по аналогии с квартилями и децилями: 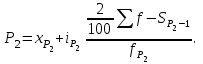 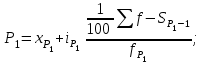 Квартили, децили и перцентили используют для расчета различных квинтильных показателей дифференциации, которыеиспользуются при изучении распределения населения по уровню доходов или работников по уровню заработной платы и т.п. Наиболее известным из них является децильный коэффициент дифференциации (табл.): 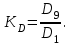 Таблица – Дифференциация доходов населения в Республике Беларусь
Источник: Статистическая база данных Национального статистического комитета Республики Беларусь [Электронный ресурс]. Режим доступа: www.belstat.gov.by. Дата доступа: 26.02.2016 г. |
