Статистика (3-5 теми). Тема зведення, класифікації та групування статистичних даних
 Скачать 333.56 Kb.
|
ТЕМА 5. ВИБІРКОВЕ СПОСТЕРЕЖЕННЯ
1. Поняття про вибіркове спостереження. Генеральна та вибіркова сукупність Під час завершення переходу до ринкової економіки вибірковий метод стає все актуальнішим. Зміни в характері економічних відносин, широке розповсюдження оренди та власності окремих колективів і осіб зумовлюють зміни функцій обліку та статистики, зменшення обсягу та спрощення звітності. Однак менеджмент потребує надійної оперативної інформації. Тому в економіці широко застосовують вибірковий метод. Нині немає жодної галузі статистики, де б не використовували цей метод. Як відомо, статистичне спостереження може бути суцільним і не-суцільним. Несуцільне спостереження найбільшого розповсюдження набуло у формі вибіркового, або, як його часто називають у літературі, репрезентативного, методу. Вибірковим називається таке спостереження, коли обстежують лише частину одиниць досліджуваної сукупності та за його результатами характеризують усю сукупність. Вибіркове спостереження застосовують у таких випадках:
Особливість вибіркового методу полягає в тому, що в основі відбору одиниць для обстеження покладено принцип рівних можливостей потрапляння одиниці генеральної сукупності у вибірку. Тому у вибіркову сукупність не можуть потрапити одиниці, що характеризуються тільки за однією ознакою. Це попереджує появу систематичних (тенденційних) помилок і вможливлює кількісну оцінку помилки репрезентативності. Як було зазначено, вибіркове спостереження багато в чому переважає суцільне, проте воно має недоліки. Результати вибіркового спостереження зазвичай не збігаються з даними суцільного, а отже вибіркове спостереження не таке точне. За допомогою вибіркового спостереження, вивчають переважно такі показники:
Вибіркове спостереження дає можливість одержати узагальнювальні показники (середні, відносні), які досить правильно характеризують усю генеральну сукупність, проте його результати майже завжди відрізняються від результатів суцільного спостереження. Сукупність одиниць, з якої провадиться вибірка, називається генеральною. Обстежувані одиниці генеральної сукупності, називають вибірковою сукупністю. Різниця між зведеними показниками вибіркової та генеральної сукупності називається помилкою вибірки (репрезентативності). Організовуючи вибіркове спостереження, важливо уникати виникнення систематичних помилок. Випадкових помилок вибірки уникнути неможливо, але за допомогою вибіркового методу (для двох схем формування вибірки: повторної та безповторної) можна визначити можливі їх межі з практично достатньою точністю та надійністю, а також регулювати їх розміри. Середня будь-якої ознаки, обчислена з усіх одиниць генеральної сукупності, називається генеральною середньою. Середня всіх одиниць вибіркової сукупності називається вибірковою середньою. Крім середньої величини як для генеральної, так і для вибіркової сукупності часто виникає потреба визначити відносний показник — частку одиниць, які мають досліджувану ознаку. Така величина в генеральній сукупності називається генеральною часткою, а у вибірковій сукупності — вибірковою часткою. Поняття, що стосуються вибіркового спостереження та перенесення результатів вибірки на генеральну сукупність, позначають такими символами:  — кількість одиниць генеральної сукупності; — кількість одиниць генеральної сукупності з однаковою ознакою; — кількість одиниць вибіркової сукупності; — кількість одиниць вибіркової сукупності з однаковою ознакою; — генеральна середня сукупності; — вибіркова середня; — генеральна частка; — вибіркова частка; — дисперсія; — середнє квадратичне відхилення; — середня помилка вибірки для середньої величини; — середня помилка для частки; — коефіцієнт довіри; — гранична похибка вибірки для середньої величини; — гранична похибка для частки.Типова задача. За даними суцільного спостереження в магазинах мікрорайону міста, 2000 продавців, із яких 1600 мають спеціальну освіту, нараховано заробітну плату в розмірі 600 тис. грн. Через тиждень проведено 10-процентне вибіркове обстеження 200 продавців, яким нараховано 60,6 тис. грн заробітної плати. У результаті вибіркового обстеження виявилося, що з 200 обстежених продавців 164 мають спеціальну освіту. За даними попереднього обстеження відомо, що середнє квадратичне відхилення становить 30 грн. Визначити середню заробітну плату та мастку продавців зі спеціальною освітою в генеральній і вибірковій сукупностях. Запишемо умову задачі за допомогою символів:  = 2000; = 1600; = 200; = 164; ФЗП = 600000 грн (фонд заробітної плати продавців мікрорайону); Фзп = 60600 грн (фонд заробітної плати повторно обстежених продавців). Потрібно визначити  , , , . Середню заробітну плату продавців у генеральній і вибірковій сукупностях визначають діленням фонду заробітної плати на чисельність продавців: Помилка вибірки (репрезентативності) дорівнює різниці між вибірковою та генеральною середніми.  Частку продавців зі спеціальною освітою в загальній чисельності продавців визначають за формулою відносної величини структури. У нашому прикладі генеральна частка  вибіркова —  Отже, частки продавців зі спеціальною освітою в генеральній сукупності становить 80 %, а у вибірковій — 82 %. Помилка вибірки для части становить  2. Середня помилка вибірки Помилки вибірки залежать насамперед від обсягу вибірки. Чим більше взято одиниць для вибірки, тим менша помилка. Якщо довести чисельність вибірки до чисельності одиниць генеральної сукупності  , то дані вибіркової сукупності дорівнюватимуть даним генеральної сукупності.Помилки вибірки, крім того, залежать і від варіації, коливання ознаки в сукупності. Чим більша варіація, тим більша помилка, і навпаки. Наприклад, якби всі 2000 продавців одержали зарплату 300 грн., то помилки не було б, бо середня заробітна плата у вибірковій сукупності була б такою самою, як і в генеральній. На практиці цього не буває, бо зазвичай є відхилення. Щоб оцінити, наскільки зведені показники вибіркової сукупності відрізняються від генеральної, потрібно обчислити не просто помилку вибірки, а середню помилку вибірки. Чому середню? Перш за все тому, що з будь-якої сукупності можна провести не одну, а багато вибірок, і їх зведені результати зазвичай не збігаються, хоча й близькі. Таблиця 1 Розподіл студентів факультету за успішністю
Обчислимо середню успішність студентів у генеральній і вибірковій сукупностях (середній бал). Середня успішність студентів у генеральній сукупності  а середня успішність у першій і другій вибіркових сукупностях — відповідно  Зазвичай після кожної вибірки її помилка набуває різних значень:   Обчислимо тепер частку студентів у генеральній і вибірковій сукупностях, які навчаються на "4" та "5":   Як бачимо, помилки вибірки для частки також різні:  Оскільки помилки вибірки — змінні величини, що можуть набувати різних значень залежно від чисельності вибірки та варіації ознак, остільки виникає потреба в обчисленні середньої помилки вибірки. Вибірка може бути повторною та безповторною. Повторною називається вибірка, коли одиниці, що вже один раз потрапили у вибірку, повертають у генеральну сукупність, і вони можуть знову бути у вибірці кілька разів. Наприклад, усі громадяни формально можуть одержати путівку в санаторій, а отримують часто одні й ті самі. Те саме можна сказати про відвідування магазину, театру, обмін валют, поїздки за кордон тощо. Безповторною називається вибірка, коли один раз відібрані одиниці для обстеження не повертають знову в генеральну сукупність, і вони не беруть участі в подальших відборах (наприклад, розіграш лотереї, народження людини, її смерть тощо). У разі безповторної вибірки помилки репрезентативності менші, ніж у разі повторної. Для визначення середньої помилки вибірки для середньої та частки в разі повторної вибірки користуються такими формулами:  у разі безповторної - 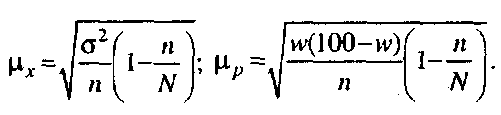 У математичній статистиці доведено, що значення середньої помилки вибірки визначають за допомогою залежності  за умови, що відома генеральна дисперсія  . Але в разі проведення вибіркового обстеження ці показники зазвичай невідомі. Тому на практиці використовують дисперсію вибіркової сукупності . При цьому виходять із того, що в разі застосування принципу випадкового відбору дисперсія достатньо великого обсягу вибірки практично збігається з дисперсією генеральної сукупності. У математичній ста-тистиці доведено таке співвідношення між дисперсіями в генеральній і вибірковій сукупностях: Згідно з ним дисперсія у вибірковій сукупності менша, ніж дисперсія в генеральній, в разів. Зі збільшенням  відношення наближається до одиниці, а — до Якщо замінити генеральну дисперсію вибірковою  , то Для показника середньої величини дисперсії кількісної ознаки у вибірці визначають за такими залежностями:  де  — частота.Середня помилка вибірки показує, наскільки в середньому вибіркова середня величина (частка) відрізняється від генеральної. її обчислюють для того, щоб перенести результати вибірки на генеральну сукупність за допомогою формул  Продемонструємо обчислення середньої помилки вибірки та перенесемо результати на генеральну сукупність. Нехай =303 грн; =2000; =200; =30 грн; = 82 Обчислимо середню помилку вибірки для середньої зарплати за формулою повторної вибірки:  і безповторної:  Отже, середня заробітна плата у вибірковій сукупності відрізняється від генеральної на 2,12 грн. в разі повторної вибірки та на 2,01 грн. — у разі безповторної. Перенесемо результати вибіркового спостереження на генеральну сукупність:  . У разі повторної вибірки  , а в разі без повторної  .Отже, середня заробітна плата продавця в генеральній сукупності лежить у межах від 300,88 до 305,12 грн. в разі повторної вибірки та в межах від 300,99 до 305,01 грн. — у разі безповторної.  Обчислимо середню помилку вибірки для частки продавців зі спеціальною освітою за формулою повторної вибірки:  і безповторної: Отже, під час визначення частки продавців зі спеціальною освітою допущено помилку 2,7 % у разі повторної вибірки та 2,6 % — у разі безповторної. Перенесемо результати вибіркового спостереження на генеральну сукупність:  . У разі повторної вибірки  , а в разі безповторної —  Отже, частка продавців зі спеціальною освітою в генеральній сукупності лежить у межах від 79,3 до 84,7 % у разі повторної вибірки, та в межах від 79,4 до 84,6 % — у разі безповторної. Математична статистика гарантує такі висновки щодо середньої заробітної плати та частки продавців зі спеціальною освітою лише з імовірністю 0,683 (див. підрозд. 9.3). Якщо дослідника влаштовує така ймовірність, обчислення завершують, а не то визначають так звану граничну помилку вибірки, що залежить від коефіцієнта довіри, кожному значенню якого відповідає конкретний показник імовірності. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||