практическая занятие. Практическое занятие 6. Темы Квадратные и иррациональные уравнения и неравенства. Метод интервалов. Степенная, показательная и логарифмическая функции. Решение тригонометрических уравнений и неравенств.
 Скачать 132.94 Kb. Скачать 132.94 Kb.
|
|
Практическое занятие 6 Темы: Квадратные и иррациональные уравнения и неравенства. Метод интервалов. Степенная, показательная и логарифмическая функции. Решение тригонометрических уравнений и неравенств. Производная функции. Исследование функции с помощью производной. Неопределенный интеграл. Определенный интеграл. Многогранники и площади их поверхностей. Объем многогранников. Элементы математической статистики. Цель занятия: закрепление навыков решения квадратных, дробно-рациональных и иррациональных уравнений и неравенств, нахождения значений показательных и логарифмических выражений; закрепление навыков решения тригонометрических уравнений и неравенств, а также задач дифференциального исчисления и интегрального исчисления; нахождения площади поверхности и объема многогранника; овладение навыками решения простейших задач математической статистики. Задание 1. (Максимальное количество баллов – 1 балл) Решите предложенные уравнения, подробно описывая ход решения (указывайте формулы, которыми пользуетесь, записывайте промежуточные результаты): 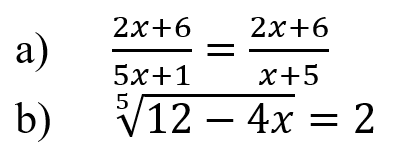 Задание 2. (Максимальное количество баллов – 1 балл) Решите предложенные неравенства методом интервалов, подробно описывая ход решения: 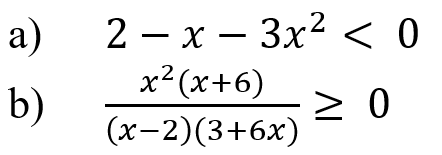 Задание 3. (Максимальное количество баллов – 2 балла) Найдите значение выражений, подробно описывая ход решения (указывайте формулы, которыми пользуетесь, записывайте промежуточные результаты): 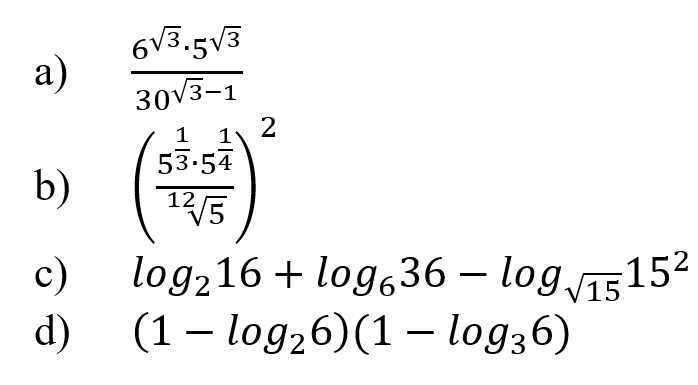 Задание 4. (Максимальное количество баллов – 2 балла) Решите предложенные уравнения, подробно описывая ход решения (указывайте формулы, которыми пользуетесь, записывайте промежуточные результаты): 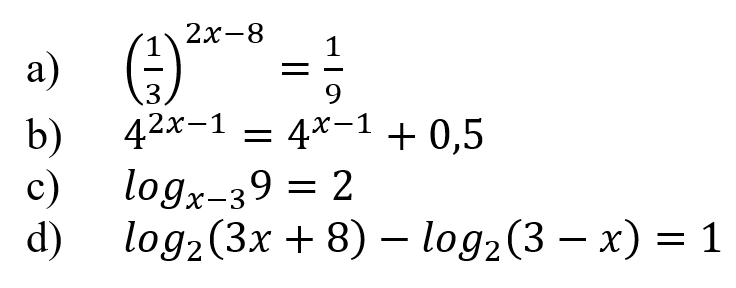 Задание 5. (Максимальное количество баллов – 2 балла) Решите предложенные неравенства, подробно описывая ход решения (указывайте формулы и положения, которыми пользуетесь, записывайте промежуточные результаты): 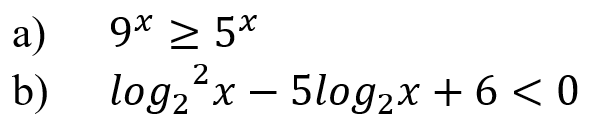 Задание 6. (Максимальное количество баллов – 3 балла) Решите предложенные тригонометрические уравнения и неравенства, подробно описывая ход решения (указывайте формулы, которыми пользуетесь, отобразите графически на единичной окружности соответствующие точки и интервалы): 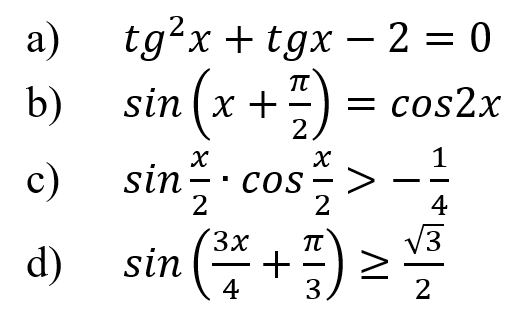 Задание 7. (Максимальное количество баллов – 2 балла) Вычислите предложенные производные функций, подробно описывая ход решения (указывайте формулы, которыми пользуетесь, записывайте промежуточные результаты): 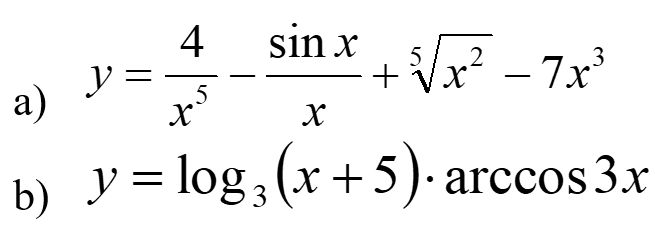 Задание 8. (Максимальное количество баллов - 4 балла) Вам предложена функция 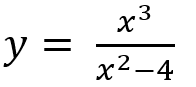 Проведите исследование, согласно схеме: 1. Найти область определения функции. 2. Найти точки пересечения с осями. 3. Исследовать функцию на четность/нечетность. 4. Найти асимптоты. 5. Найти экстремумы и интервалы монотонности функции. 6. Найти интервалы выпуклости функции и точки перегиба. 7. Найти дополнительные точки, уточняющие график. 8. Построить график. Задание 9. (Максимальное количество баллов – 2 балл) Вычислите предложенные неопределенные интегралы, подробно описывая ход решения (указывайте формулы, которыми пользуетесь, записывайте промежуточные результаты). 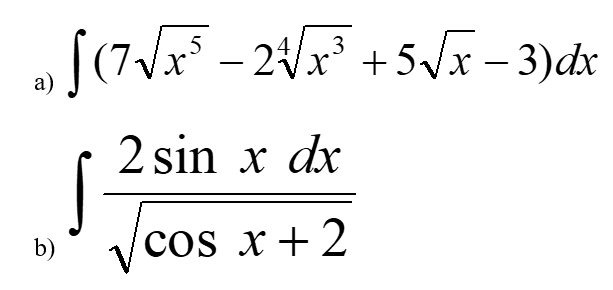 Задание 10. (Максимальное количество баллов – 2 балла) Вычислите площадь предложенной криволинейной трапеции, ограниченной графиками функций f(x) и g(x), подробно описывая ход решения (указывайте формулы, которыми пользуетесь, отобразите графики функций и получившуюся фигуру, записывайте промежуточные результаты): 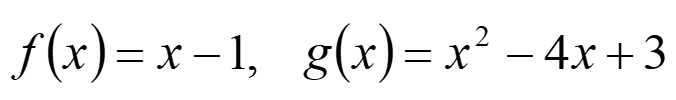 Задание 11. (Максимальное количество баллов – 1 балл) Решите предложенную задачу, подробно описывая ход решения (указывайте формулы, которыми пользуетесь, отобразите графически полученное решение): Найдите объем многогранника, вершинами которого являются точки A, A1, B1, C1 правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 6 см2, а боковое ребро равно 4 см. Задание 12. (Максимальное количество баллов – 3 балла) Изучите предложенные исходные данные, полученные при измерении:
Выполните задания с учетом исходных данных, подробно описывая ход вашего решения: Построить полигон распределения. Вычислить выборочную среднюю, дисперсию, моду, медиану. Построить выборочную функцию распределения. |
