статистическое изображение рядов распределения. Теоретическая часть. 11. Ряды распределения, их виды и графическое изображение
 Скачать 218.48 Kb. Скачать 218.48 Kb.
|
|
|
| Годы | Мощность ГЭС, млн. кВт | Трехлетняя сумма уровней для скользящего периода, млн.кВт | Трехлетняя скользящая средняя, млн.кВт |
| 1997 | 22,2 | — | — |
| 1998 | 31,4 | 94,5 | 31,5 |
| 1999 | 40,9 | 124,6 | 41,53 |
| 2000 | 52,3 | 154,9 | 51,63 |
| 2001 | 61,7 | 177,8 | 59,27 |
| 2002 | 63,8 | 189,8 | 63,27 |
| 2003 | 64,3 | — | — |
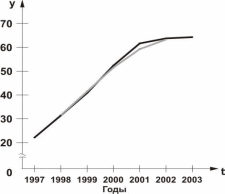
Рисунок 4. Сглаживание ряда динамики мощности ГЭС скользящей средней: линия черным цветом - фактические данные, серым цветом - сглаженные.
5. Выровняем ряд по прямой.
П
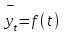 ри выравнивании по прямой линии закономерно изменяющиеся уровни динамического ряда рассчитываются как функция времени, выражающаяся уравнением:
ри выравнивании по прямой линии закономерно изменяющиеся уровни динамического ряда рассчитываются как функция времени, выражающаяся уравнением:П
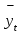 араметры аналитического уравнения выбранной линии находят, используя способ наименьших квадратов. В этом случае предполагается, что сумма квадратов отклонений фактических уровней (y) от выровненных (), т.е. расположенных на искомой линии, должна быть минимальной:
араметры аналитического уравнения выбранной линии находят, используя способ наименьших квадратов. В этом случае предполагается, что сумма квадратов отклонений фактических уровней (y) от выровненных (), т.е. расположенных на искомой линии, должна быть минимальной: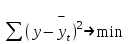
Рассмотрим технику выравнивания ряда динамики по уравнению тренда прямой:
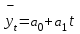
,
где t – условное обозначение времени; a0 и a1 – параметры искомой прямой.
П
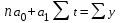 араметры a0 и a1, удовлетворяющие методу наименьших квадратов, находятся путем решения следующей системы нормальных уравнений:
араметры a0 и a1, удовлетворяющие методу наименьших квадратов, находятся путем решения следующей системы нормальных уравнений: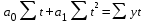 ; ;
; ;,
где y - фактические уровни ряда динамики; n – число уровней ряда;t– нумерация фактора времени.
Э
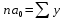 та система уравнений значительно упрощается, если значения tподобрать так, чтобы их сумма равнялась нулю. Тогда получается следующая система уравнений:
та система уравнений значительно упрощается, если значения tподобрать так, чтобы их сумма равнялась нулю. Тогда получается следующая система уравнений:;
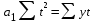
,
решая которую, получаем:
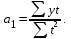
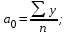
; ..
Так как у нас уровней в ряду динамики нечетное число, от отсчет ведется от середины, принятой за ноль (таблица 6.):
Таблица 6. Условные обозначения времени
| Годы | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 |
| t | -3 | -2 | -1 | 0 | +1 | +2 | +3 |
Таблица 7. Расчет параметров уравнения тренда прямой и теоретических значений ряда динамики мощности ГЭС
| Год | Фактическая мощность ГЭС, млн.кВт (y) | t | t2 | yt | |
| 1997 | 22,2 | -3 | 9 | -66,6 | 25,382 |
| 1998 | 31,4 | -2 | 4 | -62,8 | 32,95 |
| 1999 | 40,9 | -1 | 1 | -40,9 | 40,518 |
| 2000 | 52,3 | 0 | 0 | 0 | 48,086 |
| 2001 | 61,7 | +1 | 1 | 61,7 | 55,654 |
| 2002 | 63,8 | +2 | 4 | 127,6 | 63,222 |
| 2003 | 64,3 | +3 | 9 | 192,9 | 70,79 |
| Итого | 336,6 | 0 | 28 | 211,9 | 336,6 |
П
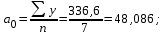 о данным таблицы находим:
о данным таблицы находим: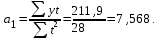
Искомое уравнение прямой будет иметь вид:
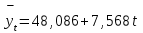
П
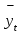 одставляем в это уравнение соответствующие значения t, находим выровненные (теоретические) уровни .
одставляем в это уравнение соответствующие значения t, находим выровненные (теоретические) уровни .Д
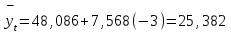 ля 1997 г. (t= - 3) получим:
ля 1997 г. (t= - 3) получим:Д
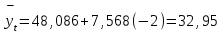 ля 1998 г. .(t= - 2) получим:
ля 1998 г. .(t= - 2) получим:Д
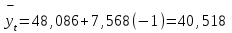 ля 1999 г. (t= - 1) получим:
ля 1999 г. (t= - 1) получим:Д
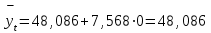 ля 2000 г. (t= 0) получим:
ля 2000 г. (t= 0) получим:Для 2001 г. (t= +1) получим:
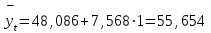
Для 2002 г. (t= +2) получим:
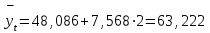
Д
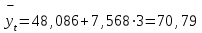 ля 2003 г. (t= +3) получим:
ля 2003 г. (t= +3) получим:7. На основе найденного уравнения тренда определим предполагаемую среднюю мощность ГЭС в 2006 г. (t=+6):
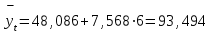 Выводы.
Выводы.
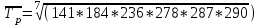
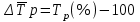
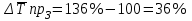
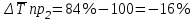
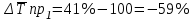
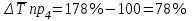
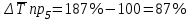
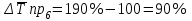
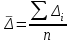
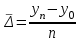 .3. Средний абсолютный прирост:
.3. Средний абсолютный прирост: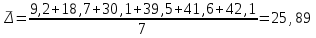
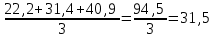 .
.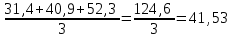 атем за 3 года, но начиная не с 1997, а с 1998 года:
атем за 3 года, но начиная не с 1997, а с 1998 года: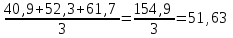 атем за 3 года, но начиная не с 1998, а с 1999 года:
атем за 3 года, но начиная не с 1998, а с 1999 года: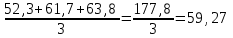 атем за 3 года, но начиная с 2000 года:
атем за 3 года, но начиная с 2000 года: