Тест. Анализ деятельности банка. Теоретические аспекты статистического анализа финансового состояния банков
 Скачать 4.55 Mb. Скачать 4.55 Mb.
|
Расчетные формулы аналитических показателей ряда динамики
Для характеристики среднего изменения определяют: Средний уровень интервального ряда с равностоящими пределами: 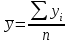 (6) (6)Средний абсолютный прирост, показывающий, насколько в среднем за анализируемый период снизился или возрос уровень ряда: 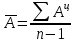 (7) (7)Средний темп роста, показывающий, насколько % или во сколько раз в среднем за анализируемый период снизился или возрос уровень ряда: 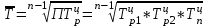 (8) (8)4. Средний темп прироста, показывающий, насколько % или во сколько раз в среднем за анализируемый период снизился или возрос уровень ряда: 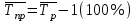 (9) (9)Одной из важнейших задач статистики является определение в рядах динамики общей тенденции развития явления. В некоторых случаях закономерность изменения явления, общая тенденция его развития явно и отчетливо отражается уровнями динамического ряда (уровни на изучаемом периоде непрерывно растут или непрерывно снижаются). Однако часто встречаются такие ряды динамики, в которых уровни ряда претерпевают самые разные изменения, и общая тенденция развития неясна. На развитие явления во времени оказывают влияние факторы, различные по характеру и силе воздействия. Одни из них оказывают практически постоянное воздействие и формируют в рядах динамики определенную тенденцию развития. Воздействие же других факторов может быть кратковременным или носить случайный характер. Поэтому при анализе динамики речь идет не просто о тенденции развития, а об основной тенденции, достаточно стабильной (устойчивой) на протяжении изучаемого этапа развития. Основная тенденция (тренд) – это главное устойчивое изменение, свободное от случайных колебаний.[10] Для характеристики основной тенденции используют следующие методы: Метод укрупнения интервалов – расчет значения по укрупненным данным. Метод скользящей средней – расчет среднего значения для нечетного числа периодов, опускаясь на один период. Метод аналитического выравнивания по прямой – составление уравнения прямой следующего вида:  (10) (10)Параметры ао и а1 находят решение системы уравнений:  (11) (11)Где у-фактические уравнения, t- время(по  рядковый номер периода или момента t). Если t =0,то: рядковый номер периода или момента t). Если t =0,то: (12) (12)Из первого уравнения  ; из второго уравнения ; из второго уравнения  1.3. Методы изучения взаимосвязи между явлениями Корреляция – это статистическая зависимость между случайными величинами, не имеющими строго функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой. [12] В экономических исследованиях часто решают задачу выявления факторов, определяющих уровень и динамику экономического процесса. Такая задача чаще всего решается методами корреляционного и регрессионного анализа. Для достоверного отображения объективно существующих в экономике процессов необходимо выявить существенные взаимосвязи и дать им количественную оценку. Этот подход требует вскрытия причинных зависимостей. Под причинной зависимостью понимается такая связь между процессами, когда изменение одного из них является следствием изменения другого. [12] Основными задачами корреляционного анализа являются: оценка силы связи и проверка статистических гипотез о наличии и силе корреляционной связи. Для измерения тесноты связи меду двумя из рассматриваемых переменных (без учета их взаимодействия с другими переменными) применяется парный коэффициент корреляции. Если известны средние квадратические отклонения (σ) анализируемых величин, то парные коэффициенты корреляции рассчитывают по формулам:  ; (13) ; (13) ; (14) ; (14) . (15) . (15)В реальных условиях все переменные, как правило, взаимосвязаны. Теснота этой связи определяется частными коэффициентами корреляциями, которые характеризуют степень и влияние одного из аргументов на функцию при условии, что остальные независимые переменные закреплены на постоянном уровне. Частный коэффициент корреляции первого порядка между признаками x1и y при исключении влияния признака x2 вычисляют по формуле: 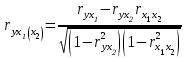 ; (16) ; (16)то же – зависимость y от x2 при исключении влияния x1. Показателем тесноты связи, устанавливаемой между результативным и двумя или более факторными признаками, является совокупный коэффициент множественной корреляции 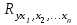 . В случае линейной двухфакторной связи совокупный коэффициент множественной корреляции может быть рассчитан по формуле: . В случае линейной двухфакторной связи совокупный коэффициент множественной корреляции может быть рассчитан по формуле: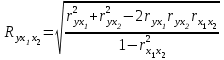 , (17) , (17)где r – линейные коэффициенты корреляции (парные); подстрочные индексы показывают, между какими признаками они исчисляются. Совокупный коэффициент множественной корреляции измеряет одновременное влияние факторных признаков на результативный. Его значения находятся в пределах -1 до +1. Чем меньше наблюдаемые значения изучаемого показателя отклоняются от линии множественной регрессии, тем корреляционная связь интенсивнее, а следовательно, значение R ближе к единице. [11] Величина R2, которая показывает, какая доля вариации изучаемого показателя объясняется влиянием факторов, включенных в уравнение множественной регрессии, называется совокупным коэффициентом множественной детерминации. Значение совокупного коэффициента множественной детерминации находится в пределах от 0 до 1. Поэтому, чем ближе R2 к единице, тем вариация изучаемого показателя в большей мере характеризуется влиянием отобранных факторов. [7] Показатели множественной регрессии и корреляции могут оказаться подверженными действию случайных факторов. Общую оценку адекватности уравнения получают с помощью дисперсионного F-критерия Фишера: 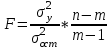 , (18) , (18)где m – число параметров в уравнении регрессии. Не все факторы, влияющие на экономические процессы, являются случайными величинами, поэтому при анализе экономических явлений обычно рассматриваются связи между случайными и неслучайными величинами. Такие связи называются регрессионными, а метод математической статистики, их изучающий, называется регрессионным анализом. Уравнение однофакторной регрессионной связи имеет вид:  , (19) , (19)где  – теоретические значения результативного признака; – теоретические значения результативного признака;а0и а1– параметры уравнения регрессии. При исследовании влияния на результативный фактор нескольких факторных применяется формула множественной регрессии с n-факторами:  (20) (20)Чтобы иметь представление о силе влияния отдельных факторных признаков на результативный, вычисляют следующие коэффициенты: Коэффициент эластичности:  , (21) , (21)где 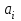 - коэффициент регрессии при i-ом факторе, - коэффициент регрессии при i-ом факторе, 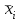 - среднее значение i-го фактора, - среднее значение i-го фактора, 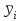 - среднее значение результативного признака. - среднее значение результативного признака.Коэффициент эластичности показывает, на сколько процентов изменяется результативный признак при изменении факторного на 1%. 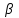 -коэффициент: -коэффициент: 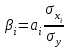 , (22) , (22)где 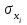 - среднее квадратическое отклонение i-го фактора; - среднее квадратическое отклонение i-го фактора; 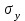 - среднее квадратическое отклонение результативного признака, которые, в свою очередь, находят по следующим формулам: - среднее квадратическое отклонение результативного признака, которые, в свою очередь, находят по следующим формулам: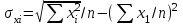 (23) (23)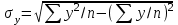 (24) (24)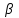 -коэффициент показывает, на какую часть среднего квадратического отклонения изменяется результативный признак с изменением соответствующего факторного. -коэффициент показывает, на какую часть среднего квадратического отклонения изменяется результативный признак с изменением соответствующего факторного.Корреляционный анализ и регрессионный анализ являются смежными разделами математической статистики и предназначаются для изучения по выборочным данным статистической зависимости ряда величин. Корреляция и регрессия тесно связаны между собой: первая оценивает силу (тесноту) статистической связи, вторая исследует ее форму. И корреляция, и регрессия служат для установления соотношений между явлениями и для определения наличия или отсутствия связи между ними. Пользуясь методами корреляционно-регрессионного анализа, аналитики измеряют тесноту связей показателей с помощью коэффициента корреляции. При этом обнаруживаются связи, различные по силе (сильные, слабые, умеренные и др.) и различные по направлению (прямые, обратные). Если связи окажутся существенными, то целесообразно будет найти их математическое выражение в виде регрессионной модели и оценить статистическую значимость модели. В экономике значимое уравнение используется, как правило, для прогнозирования изучаемого явления или показателя. [6] Следует иметь ввиду, что вероятностное или статистическое решение любой экономической задачи должно основываться на подробном осмыслении исходных математических понятий и предпосылок, корректности и объективности сбора исходной информации, в постоянном сочетании с теснотой связи экономического и математико-статистического анализа. Для применения корреляционного анализа необходимо, чтобы все рассматриваемые переменные были случайными и имели нормальный закон распределения. Причем выполнение этих условий необходимо только при вероятностной оценке выявленной тесноты связи. Экономические данные почти всегда представлены в виде таблиц. Числовые данные, содержащиеся в таблицах, обычно имеют между собой явные (известные) или неявные (скрытые) связи. Явно связаны показатели, которые получены методами прямого счета, т. е. вычислены по заранее известным формулам (проценты выполнения плана, уровни, удельные веса, отклонения в сумме, отклонения в процентах, темпы роста, темпы прироста, индексы и т. д.). Связи же второго типа (неявные) заранее неизвестны. Однако необходимо уметь объяснять и предсказывать (прогнозировать) сложные явления для того, чтобы управлять ими. Поэтому специалисты с помощью наблюдений стремятся выявить скрытые зависимости и выразить их в виде формул, т. е. математически смоделировать явления или процессы. Одну из таких возможностей предоставляет корреляционно-регрессионный анализ.[9] Регрессионный анализ называют основным методом современной математической статистики для выявления неявных и завуалированных связей между данными наблюдений. Электронные таблицы делают такой анализ легко доступным. Таким образом, регрессионные вычисления и подбор хороших уравнений – это ценный, универсальный исследовательский инструмент в самых разнообразных отраслях деловой и научной деятельности (маркетинг, торговля, медицина и т. д.). Усвоив технологию использования этого инструмента, можно применять его по мере необходимости, получая знание о скрытых связях, улучшая аналитическую поддержку принятия решений и повышая их обоснованность. Корреляционно-регрессионный анализ считается одним из главных методов в маркетинге, наряду с оптимизационными расчетами, а также математическим и графическим моделированием трендов (тенденций). Широко применяются как однофакторные, так и множественные регрессионные модели. Использование возможностей современной вычислительной техники, оснащенной пакетами программ машинной обработки статистической информации на ЭВМ, делает практически осуществимым оперативное решение задач изучения взаимосвязи показателей биржевых ставок методами корреляционно-регрессионного анализа. При машинной обработке исходной информации на ЭВМ, оснащенных пакетами стандартных программ ведения анализов, вычисление параметров применяемых математических функций является быстро выполняемой счетной операцией. Глава 2. Применение статистических методов для анализа динамики финансового состояния АКБ «Альфа-банк» 2.1. Общая характеристика АКБ «Альфа-Банк» Альфа-Банк — крупнейший частный банк России, успешно работающий с 1990 года. Организационно-правовая форма банка – открытое акционерное общество. Альфа-Банк является высокотехнологичным универсальным банком, предоставляющим полный комплекс услуг корпоративным и частным клиентам. Банк входит в число самых надежных и диверсифицированных финансовых структур России. Альфа-Банк входит в пятерку крупнейших российских банков по величине активов и собственного капитала. По данным аудированной финансовой отчетности (МСФО) за 2004 год, активы группы «Альфа-Банк», куда входят ОАО «Альфа-Банк», дочерние банки и финансовые компании, составили 7 млрд. долларов США, чистая прибыль — 153 млн. долларов США, собственный капитал — 708 млн. долларов США, кредитный портфель — 4,7 млрд. долларов США. [13] Альфа-Банк — один из немногих российских банков, где проводится международная аудиторская проверка с 1993 года. Стратегическое направление деятельности Альфа-Банка — розничный бизнес. В 2003 году Альфа-Банк представил новый стандарт работы с частными клиентами и компаниями малого бизнеса. Сегодня в Москве открыто 28 отделений комплексного банковского обслуживания частных лиц. В 2004 году Банк вышел на рынок потребительского кредитования. Успешно развивается инвестиционный бизнес Альфа-Банка. Банк эффективно работает на рынках капитала, ценных бумаг с фиксированной доходностью, валютном и денежном рынках, в сфере операций с деривативами. Банк стабильно удерживает позицию одного из ведущих операторов и маркет-мейкеров на внешнем рынке суверенных российских облигаций и долговых инструментов российского корпоративного сектора. Альфа-Банк создал разветвленную филиальную сеть — важнейший канал распространения услуг и продуктов. В Москве, регионах России и за рубежом открыто около 110 отделений и филиалов банка, в том числе дочерние банки на Украине, в Казахстане и Нидерландах, а также в Башкортостане и Татарстане. Представительства банка действуют в Великобритании и США. Долгосрочные текущие рейтинги Альфа-Банка — Fitch («B+» со стабильным прогнозом), Moody’s («Ba2» с позитивным прогнозом) и Standard & Poor’s («BB−» со стабильным прогнозом).[15] Альфа-Банк является членом Попечительского Совета Большого театра, членом Корпоративного клуба WWF России, продолжает реализацию образовательной программы для российских школьников «Альфа-Шанс», оказывает финансовую поддержку благотворительной программе спасения тяжелобольных детей «Линия жизни». Руководство Альфа-Банка составляют люди, имеющие обширный опыт работы, как в России, так и за рубежом. Многие из них получили образование в наиболее авторитетных зарубежных и отечественных университетах и бизнес школах, имеют ученые степени и являются авторами большого числа научных работ и статей. Руководители различных подразделений банка занимали управленческие должности в крупнейших российских и зарубежных финансовых структурах, при Правительстве России и субъектов Российской Федерации. Значительный вклад в успехи банка вносят также иностранные специалисты с их богатым опытом работы в западных компаниях и на международных рынках, применение и адаптация которого к российским условиям является важной составной частью стратегии развития банка.[14] 2.2. Расчет аналитических и средних показателей Для комплексной оценки динамики финансового состояния АКБ “Альфа-Банк” необходимо провести анализ по нескольким группам показателей: Показатели анализа и оценки качества активов; Показатели оценки финансовой устойчивости банка; Показатели анализа и оценки платежеспособности банка; Для статистической оценки достаточно будет проанализировать лишь некоторые нормативы и коэффициенты. Проанализируем динамику следующих показателей финансового состояния: рентабельности капитала; соотношения высоко ликвидных активов и привлеченных средств; общая кредитная активность; дееспособность; эффективности использования привлеченных средств по доходам; используя аналитические и средние показатели ряда динамики, расчетные формулы которых представлены в таблице 1 и расчетных формулах (6),(7), (8), (9). Таблица 2 Динамика показателя рентабельности капитала
Рассчитаем средние показатели: 1. Средний уровень ряда: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

