Курсовая Управление финансовым риском. Теоретические аспекты управления финансового риска
 Скачать 220.5 Kb. Скачать 220.5 Kb.
|
|
Глава 2. Методологические основы управления рисками. 2.1. Оценка риска. Риски различных проектов характеризуются вероятными значениями получения определенных результатов. Но, как уже говорилось, принятие решений происходит в условиях неопределенности. Поэтому менеджер обязан рассмотреть несколько сценариев развития событий и выбрать из них наиболее близкий к оптимальному. По каждому из сценариев следует определить ожидаемый результат и оценить его вероятность. Степень отклонения результата от наиболее желательного характеризует риск проекта. Рассмотрим два инвестиционных проекта, по которым известна ожидаемая доходность и вероятность ее достижения (табл. 1). Таблица 1. Ожидаемая доходность проекта
В таблице 1 представлены три варианта (сценария) возможного развития событий: пессимистический, средний и оптимистический. Определена также вероятность их наступления. Сумма вероятностей равна единице. Вероятность наступления какого-либо события менеджер оценивает на основе статистических данных за прошедший период с учетом мнений экспертов или опираясь на собственные прогнозы. Так, если прогнозируется событие, которое уже имело место в прошлом, менеджер, руководствуясь статистическими материалами, может довольно точно определить вероятность его наступления. Взять, к примеру, компанию, которая страхует клиентов от несчастного случая. Если в прошлом на 1000 застрахованных было зафиксировано 25 несчастных случаев, то вероятность этого события можно оценить как 2,5%. При прогнозировании сложных экономических ситуаций или при оценке принципиально новых инвестиционных проектов статистика отсутствует. В этих случаях менеджеры вынуждены прибегать к оценкам экспертов, финансовых консультантов, к результатам научных исследований и собственного опыта. В этом случае чрезвычайно важен квалифицированный отбор экспертов и корректная обработка их мнений. Только так можно получить объективный результат. Имея экспертную оценку вероятности по каждому из сценариев, можно определить наиболее вероятный исход по каждому из проектов. Для этого рассчитывается ожидаемая доходность (В). Это делается по формуле: где Дi — доходность по сценарию i; pi — вероятность развития событий по сценарию i; n — общее число возможных сценариев. Наиболее вероятный результат, исходя из возможных сценариев, для каждого из проектов составит: ДА = 0,25· 20 + 0,5 · 30 + 0,25 · 40 = 30%; ДB = 0,25 · 10 + 0,5 · 30 + 0,25 · 50 = 30%. Итак, наиболее вероятная доходность по проекту А и проекту В будет одинаковой, и составит 30%. Однако разброс (вариация) ожидаемых доходностей по проекту В больше. Он колеблется от 10 до 50%. По проекту А разброс доходностей ниже: от 20 до 40%. Уже на основе этих данных можно сделать предварительный вывод, что проект В является более рискованным. Здесь отклонение ожидаемых доходностей от наиболее вероятного результата значимее. Но как оценить степень риска? Для этого необязательно строить графики оцениваемых показателей для всех проектов. Достаточно использовать такие измерители, как дисперсия, среднеквадратическое (стандартное) отклонение, коэффициент вариации. Дисперсия характеризует степень разброса возможных результатов от наиболее вероятного значения, присущего проекту. Дисперсия (δ2 ) дискретного распределения рассчитывается по формуле: На основе данных, представленных в таблице 1, определим дисперсию для проектов А и В: 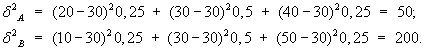 Как видим, проект В имеет более высокое значение дисперсии, и его поэтому можно оценить как более рискованный. Если менеджеры не склонны рисковать, то они отдадут предпочтение проекту А. На основе показателя дисперсии рассчитывают среднеквадратическое (стандартное) отклонение — статистическую меру вариации или широты распределения: 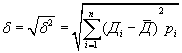 . .Стандартное отклонение измеряется в тех же единицах, что и оцениваемый показатель. Если мы пытаемся оценить доходность в процентах, то и стандартное отклонение также будет измеряться в процентах. В нашем примере стандартное отклонение для проекта А равно Итак, на основе показателей дисперсии и стандартного отклонения можно сделать вывод о большей рискованности проекта В. Данный вывод абсолютно справедлив, поскольку наиболее вероятная доходность по обоим рассматриваемым проектам одинакова и составляет 30%. А как быть в том случае, если по одному из проектов доходность и стандартное отклонение выше, чем по другому. Рассмотрим пример данных по проекту I и проекту II (табл. 2). Таблица 2 Риск и доходность по проектам (цифры условные), %
Проект I является более доходным по сравнению с проектом II, но одновременно он имеет и большую степень риска. Стандартное отклонение по проекту составляет 7,5%, а по проекту II — только 6,1%. Для принятия решения в данном случае необходимо рассчитать коэффициент вариации. Коэффициент вариации показывает меру относительной рискованности и характеризует риск на единицу наиболее вероятного результата. Коэффициент вариации (CV) рассчитывается как отношение стандартного отклонения к ожидаемому результату: В рассматриваемом примере коэффициент вариации для проекта I равен 7,5 : 30 = 0,25. Для проекта II характерна иная цифра: 6,1 : 25 = 0,24. Чем выше коэффициент вариации, тем больше степень риска на единицу результата. Следовательно, проект I, имеющий более высокий коэффициент вариации, является более рискованным. Несмотря на то, что проект I предполагает более высокую доходность, грамотный финансист предпочтет проект II. Здесь относительный риск (на единицу доходности) все-таки ниже. 2.2. Экономико-статистические методы Древо вероятностей. Измерение риска на основе дисперсии базируется на показателях вероятности наступления события по каждому из рассматриваемых сценариев. Однако оценка события и вероятность его наступления со временем меняются, поскольку трансформируются и внутренние факторы, оказывающие влияние на деятельность компании. По прошествии нескольких этапов появляются промежуточные результаты. Это позволяет более точно оценивать вероятность наступления последующих событий. Как правило, результат, полученных на первом этапе, оказывает влияние на итоги всех последующих. Словом, существует определенная зависимость между результатами, полученными в разные периоды осуществления проекта. Понятно, что результат первого периода неизбежно обусловливает ряд возможных вариантов развития событий в следующем периоде. Если же в ходе первого периода будет достигнут другой результат из-за развития событий по иному сценарию, то в дальнейшем появится другое множество вариантов. Для оценки временного фактора, когда меняется математическое ожидание и дисперсия вероятного распределения по мере перехода от одного этапа к другому, строится древо вероятностей (рис. 2). 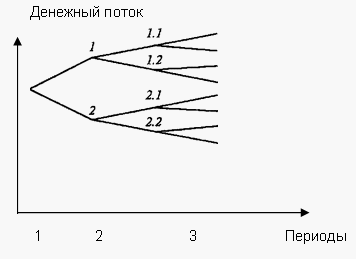 Рис. 2. Древо вероятностей. Где: 1, 2 — исходные вероятности, соответственно, лучшая и худшая; 1.1, 2.1 — условные лучшие вероятности; 1.2, 2.2 — условные худшие вероятности. По оси ординат показывается результирующий показатель проекта, в качестве которого может выступать доходность, денежный поток и т.п. На рис. 8.1 в качестве результирующего показателя рассматривается денежный поток: чем он больше, тем эффективнее проект. На рисунке представлены денежные потоки в течение трех периодов. По истечении первого периода могут быть достигнуты два результата: лучший — верхняя ветвь и худший — нижняя ветвь. Каждый из полученных результатов, в свою очередь, дает несколько последующих вариантов, так как при достижении лучшего варианта по итогам первого периода развитие будет осуществляться по одному сценарию, а в случае получения худшего результата — по другому. Аналогичная картина наблюдается при завершении второго периода и переходе к третьему периоду. В рассматриваемом примере начало первого периода не зависит от событий, которые были прежде. Вероятные результаты получаются при завершении первого периода (первые две ветви). Их называют исходными вероятностями. Для всех последующих периодов результаты зависят от развития предыдущих событий. Поэтому вероятности, соответствующие в нашем примере второму и третьему периодам, называют условными. Следовательно, если изучить цепочку исходной и условных вероятностей в их единстве, то получим совместную вероятность развития событий. Пример 1 Рассмотрим пример расчета чистых денежных потоков по проекту для двух периодов. Первоначальные вложения составили 20 млн руб. в период 0. В результате этих вложений возможны два варианта денежных потоков в 1-м периоде. С вероятностью 0,4 будет получен убыток в 10 млн руб. и с вероятностью 0,6 — положительный денежный поток, равный 15 млн руб. Отрицательный поток на 1-м периоде в размере 10 млн руб. вызывает во 2-м периоде с вероятностью 0,3 денежный поток, равный 12 млн руб., и с вероятностью 0,7 — поток, равный 22 млн руб. Положительный поток в размере 15 млн р., в свою очередь, на втором этапе с вероятностью 0,4 вызывает денежный поток в сумме 30 млн руб. и с вероятностью 0,6 — денежный поток, равный 40 млн руб. Таким образом, исходная вероятность в размере 0,4 разделяется на совместные вероятности 0,12 и 0,28, а исходная вероятность 0,6 — на 0,24 и 0,36. Таблица 3. Расчет древа вероятностей
На основе построенного древа вероятностей можно рассчитать чистые текущие стоимости денежных потоков по каждой ветви, используя безрисковую ставку дисконтирования по формуле: где NPVi — чистая текущая стоимость денежных потоков по ветви i; C0 — начальные инвестиции в период 0; С — чистый денежный поток в соответствующий период; 1 ... n — число периодов; r — безрисковая ставка дисконтирования. В представленной формуле C0 берется со знаком «-», что свидетельствует об оттоке средств с предприятия в виде произведенных инвестиций. Если в рассматриваемом примере безрисковую ставку принять на уровне 10%, то для первой ветви чистая текущая стоимость денежных потоков составит: Для четвертой ветви денежные потоки представлены поступлениями в размере 15 млн руб. в 1-м периоде и 40 млн руб. во 2-м периоде. Чистая текущая стоимость этих денежных потоков рассчитывается по формуле: На основе рассчитанных NPV денежных потоков и совместной вероятности для каждой ветви можно определить математическое ожидание чистой текущей стоимости: где NPV — математическое ожидание (наиболее вероятный результат) чистой текущей стоимости денежных потоков по проекту; NPVi — чистая текущая стоимость денежных потоков по i-й ветви; pi — совместная вероятность для i-й ветви; i = 1, ... х — число ветвей. В таблице 4 представлен расчет чистых текущих стоимостей по каждой ветви и математическое ожидание. Таблица 4 Расчет математического ожидания чистой текущей стоимости денежных потоков (цифры условные)
Математическое ожидание, рассчитанное как средневзвешенная величина чистых текущих стоимостей по каждой ветви, где в качестве весов выступает совместная вероятность (сумма последнего столбца таблицы), в нашем примере составляет 8,71 млн руб. На основе математического ожидания можно рассчитать дисперсию, стандартное отклонение и коэффициент вариации для данного проекта. Компания, обладая определенным запасом финансовых ресурсов, планирует их распределение для осуществления ряда инвестиционных проектов, в результате чего формируется инвестиционный портфель. При управлении портфелем появляется присущий ему комбинированный (совокупный) риск. Методы измерения и оценки риска портфеля несколько отличаются от оценки риска конкретного инвестиционного проекта. Портфельная теория была разработана У. Шарпом и получила широкое применение в практике управления инвестициями. Наиболее распространенной сферой использования портфельной теории являются инвестиции в ценные бумаги. У. Шарп выделил две составляющие риска любого актива: 1) систематический (рыночный); 2) несистематический (специфический). Систематический (рыночный) риск обусловлен общеэкономическими факторами. Он присущ рынку в целом и возникает по не зависящим от компании причинам. Данный риск не поддается диверсификации, поэтому его называют недиверсифицируемы. Несистематический (специфический) риск обусловлен специфическими особенностями эмитента, которые можно нейтрализовать путем включения в портфель ценных бумаг различных эмитентов. Поэтому данный вид риска называют диверсифицируемым. Общий рис включает в себя рыночный и специфический риски. Если специфического риска можно избежать, сформировав хорошо диверсифицируемый портфель, то рыночный риск присутствует всегда. C увеличением числа активов в портфеле уменьшается специфический риск. Подавляющая часть несистематического риска устраняется при включении в портфель 15—20 видов ценных бумаг. Ценные бумаги различных эмитентов по-разному реагируют на изменение общеэкономической ситуации. Одни акции более устойчивы к колебаниям рынка, другие — менее. Те ценные бумаги, которые изменяются в большей степени, чем меняется рынок, обладают повышенной чувствительностью. В связи с этим систематический риск конкретной ценной бумаги отличается от систематического риска для рынка в целом. Мерой систематического риска является коэффициент β (β-фактор), который показывает уровень изменчивости актива по отношению к рынку (усредненному активу). В качестве рыночного портфеля берутся фондовые индексы, включающие в себя акции наиболее крупных компаний. В США, например, такими индексами являются индекс S & P-500, индексы Доу—Джонса, индекс Нью-Йоркской фондовой биржи; в Великобритании — семейство индексов FT; в Японии — индексы NIKKEI; в Германии — индексы DAX; в России — индекс РТС (Российской торговой системы) и сводный индекс ММВБ (Московской межбанковской валютной биржи). Коэффициент β рассчитывается по формуле: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
