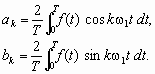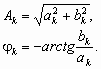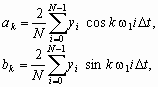работа 5. Теоретические сведения

• Название: Теоретические сведения
• Анкор: работа 5
• Дата: 25.11.2022
• Размер: 104.85 Kb.
• Имя файла: Laboratornaya_rabota_5_3.docx
• Тип: Лабораторная работа; #812086

Лабораторная работа 5
Спектральный анализ и синтез

 ЦЕЛЬ РАБОТЫ.

1.Изучение основных определений и положений представления сигналов в частотной области.

2.Изучение методов спектрального анализа.

3.Представление функций рядом Фурье.

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Одним из фундаментальных положений математики, нашедшим широкое применение во многих прикладных задачах (процессы передачи информации, в теории электротехники, в исследовании движения машин, в теории корабля и др.), является возможность описания любой периодической функции f(t) с периодом Т, удовлетворяющей условиям Дирихле (согласно теореме Дирихле периодическая функция должна иметь конечное число разрывов и непрерывность производных между ними.), с помощью тригонометрического ряда Фурье:

((1)

где  ₁ = 2 /T - частота повторения (или частота первой гармоники); k - номер гармоники. Этот ряд содержит бесконечное число косинусных или синусных составляющих - гармоник, причем амплитуды этих составляющих a_k и b_k являются коэффициентами Фурье, определяемыми интегральными выражениями:

((2) ((3)

Помимо упомянутой формы ряд Фурье можно представить в виде

((4)

 

где амплитуда А_k и фаза _k гармоник определяются выражениями:

((5) ((6)

Гармонический анализ и синтез

 

Гармоническим анализом называют разложение функции f(t), заданной на отрезке [0, Т] в ряд Фурье или в вычислении коэффициентов Фурье a_k и b_k по формулам (2) и (3).

Гармоническим синтезом называют получение колебаний сложной формы путем суммирования их гармонических составляющих (гармоник) (Рисунок 1).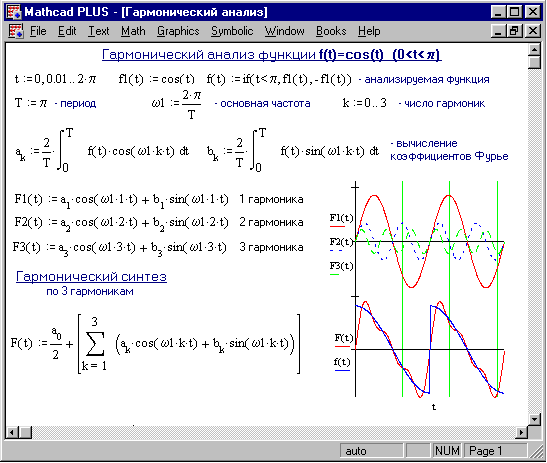

 



Рисунок 1. Гармонический синтез

 

 

 

 Классический спектральный анализ

 

Спектром временной зависимости (функции) f(t) называется совокупность ее гармонических составляющих, образующих ряд Фурье. Спектр можно характеризовать некоторой зависимостью А_k(спектр амплитуд) и  _k(спектр фаз) от частоты  _k = k₁.

 

Спектральный анализ периодических функций заключается в нахождении амплитуды А_kи фазы  _kгармоник (косинусоид) ряда Фурье (4). Задача, обратная спектральному анализу, называется спектральным синтезом (Рисунок 2).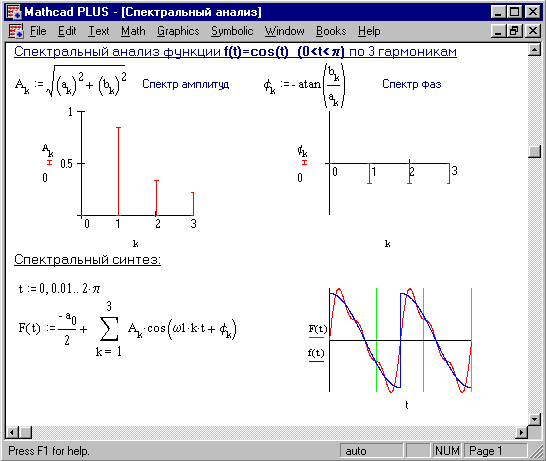

 



Рисунок 2. Классический спектральный анализ и синтез

 

Слово “классический” тут означает, что коэффициенты Фурье вычисляются прямым интегрированием тем методом, который используется в Mathcad.

 

Численный спектральный анализ

 

Численный спектральный анализ заключается в нахождении коэффициентов a₀, a₁, ..., a_k,  b₁, b₂, ..., b_k (или A₁, A₂, ..., A_k,  ₁,  ₂, ...,  _k) для периодической функции y = f(t), заданной на отрезке [0, Т] дискретными отсчетами. Он сводится к вычислению коэффициентов Фурье по формулам численного интегрирования для метода прямоугольников (см. Лабораторную работу 5)

(7)   (8)

где  t = T / N - шаг, с которым расположены абсциссы y = f(t).

 

Спектральный анализ на основе быстрого преобразования Фурье

 

Встроенные в Mathcad средства быстрого преобразования Фурье (БПФ) существенно упрощают процедуру приближенного спектрального анализа. БПФ - быстрый алгоритм переноса сведений о функции, заданной 2^m (m - целое число) отсчетами во временной области, в частотную область. Если речь идет о функции f(t), заданной действительными отсчетами, следует использовать функцию fft.

fft(v)

Возвращает прямое БПФ 2m-мерного вещественнозначного вектора v, где v - вектор, элементы которого хранят отсчеты функции f(t).

Результатом будет вектор А размерности 1 + 2^m - 1 с комплексными элементами - отсчетами в частотной области. Фактически действительная и мнимая части вектора есть коэффициенты Фурье a_k и b_k, что существенно упрощает их получение.

 

Функция ifft реализует обратное БПФ:

ifft(v)

Возвращает обратное БПФ для вектора v с комплексными элементами. Вектор v имеет 1 + 2m - 1 элементов.

Результатом будет вектор А размерности 2^m с действительными элементами.

На Рисунке 3 показано применение БПФ для спектрального анализа и синтеза импульса.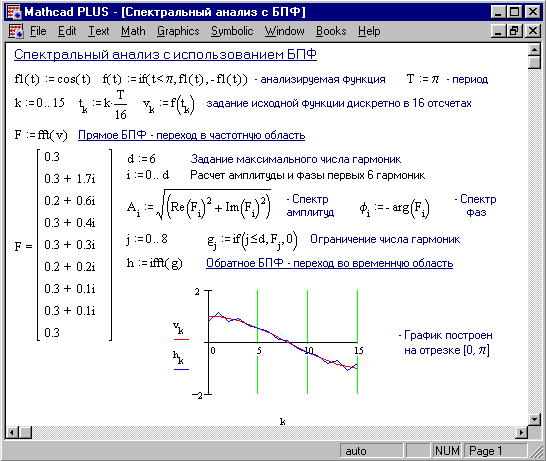

 



Рисунок 3. Спектральный анализ с использованием БПФ

 


Фильтрация аналоговых сигналов

 

Под фильтрацией подразумевается выделение полезного сигнала из его смеси с мешающим сигналом - шумом. Наиболее распространенный тип фильтрации - частотная фильтрация. Если известна область частот, занимаемых полезным сигналом, достаточно выделить эту область и подавить те области, которые заняты шумом.

Рисунок 4 иллюстрирует технику фильтрации с применением БПФ. Сначала синтезируется исходный сигнал, представленный 128 отсчетами вектора v. Затем к этому сигналу присоединяется шум с помощью генератора случайных чисел (функция rnd) и формируется вектор из 128 отсчетов зашумленного сигнала.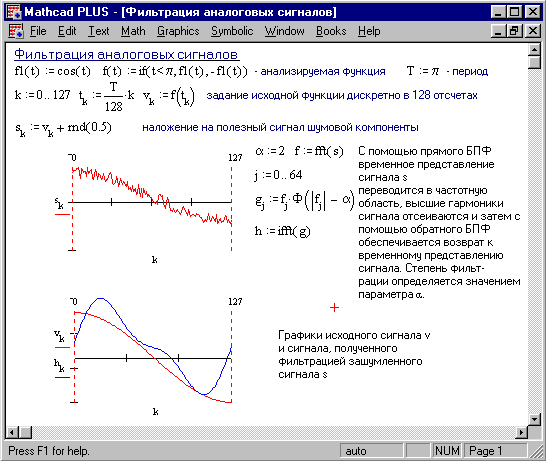

 

 



Рисунок 4. Фильтрация аналоговых сигналов

 

Используя прямое БПФ, сигнал с шумом преобразуется из временной области с частотную, что создает вектор f из 64 частотных составляющих. Затем выполняется фильтрующее преобразование, эффективность которого оценивается параметром . Фильтрующее преобразование удобно выполнять с помощью функции Хевисайда

Ф(х)	Ступенчатая функция Хевисайда. Возвращает 1, если х   0; иначе 0.

Отфильтрованный сигнал (вектор g) подвергается обратному БПФ и создает вектор выходного сигнала h.

Сравнение временных зависимостей исходного и выходного сигналов, показывает, что выходной сигнал почти полностью повторяет входной и в значительной мере избавлен от высокочастотных шумовых помех, маскирующих полезный сигнал.

 

Задание для лабораторной работы 5

 

1. Вычислить первые шесть пар коэффициентов разложения в ряд Фурье функции f(t) на отрезке [0, 2 ].

Построить графики 1, 2 и 3 гармоник.

Выполнить гармонический синтез функции f(t) по 1, 2 и 3 гармоникам. Результаты синтеза отобразить графически.

Варианты задания

 

№ варианта	f(t)	№ варианта	f(t)	№ варианта	f(t)
1		6	cos t cos sin t	11
2		7		12
3		8		13
4		9	 sin t+  sin 2t |	14
5	cos e |sin 3 t|	10		15	cos (sin t)

2. Выполнить классический спектральный анализ и синтез функции f(t). Отобразить графически спектры амплитуд и фаз, результат спектрального синтеза функции f(t).

3. Выполнить численный спектральный анализ и синтез функции f(t). Для этого необходимо задать исходную функцию f(t) дискретно в 32 отсчетах. Отобразить графически спектры амплитуд и фаз, результат спектрального синтеза функции f(t).

4. Выполнить спектральный анализ и синтез функции f(t) с помощью БПФ. Для этого необходимо:

• 
  задать исходную функцию f(t) дискретно в 128 отсчетах;
  
• 
  выполнить прямое БПФ с помощью функции fft и отобразить графически найденные спектры амплитуд и фаз первых шести гармоник;
  
• 
  выполнить обратное БПФ с помощью функции ifft и отобразить графически результат спектрального синтеза функции f(t).
  

5. Выполнить фильтрацию функции f(t) с помощью БПФ:

• 
  синтезировать функцию f(t) в виде полезного сигнала, представленного 128 отсчетами вектора v;
  
• 
  к полезному сигналу v присоединить шум с помощью функции rnd (rnd(2) - 1) и сформировать вектор из 128 отсчетов зашумленного сигнала s;
  
• 
  преобразовать сигнал с шумом s из временной области в частотную, используя прямое БПФ (функция fft). В результате получится сигнал f из 64 частотных составляющих;
  
• 
  выполнить фильтрующее преобразование с помощью функции Хевисайда (параметр фильтрации  = 2);
  
• 
  с помощью функции ifft выполнить обратное БПФ и получить вектор выходного сигнала h;
  
• 
  построить графики полезного сигнала v и сигнала, полученного фильтрацией зашумленного сигнала s.