Теоретический материал Что такое система счисления

• Название: Теоретический материал Что такое система счисления
• Дата: 17.09.2022
• Размер: 202.83 Kb.
• Имя файла: 2_.docx
• Тип: Документы; #681273
• страница: 2 из 5

5. Почему в компьютерах используются также восьмеричная и шестнадцатеричная системы счисления?

Двоичная система, удобная для компьютеров, для человека неудобна из-за ее громоздкости и непривычной записи.

Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Однако, чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы.

Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и 16 — соответственно, третья и четвертая степени числа 2).
 

Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).

Например:


 

Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на  триады  (для восьмеричной) или  тетрады  (для шестнадцатеричной)  и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой.

Например,

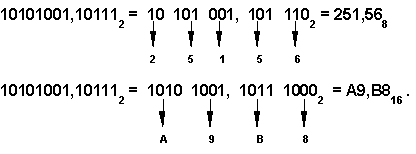
6. Как перевести целое число из десятичной системы в любую другую позиционную систему счисления?

Для перевода целого десятичного числа  N  в систему счисления с основанием  q  необходимо  N  разделить с остатком ("нацело") на  q , записанное в той же десятичной системе. Затем неполное частное, полученное от такого деления, нужно снова разделить с остатком на  q , и т.д., пока последнее полученное неполное частное не станет равным нулю. Представлением числа N  в новой системе счисления будет последовательность остатков деления, изображенных одной q-ичной цифрой и записанных в порядке, обратном порядку их получения.

Пример: Переведем число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:



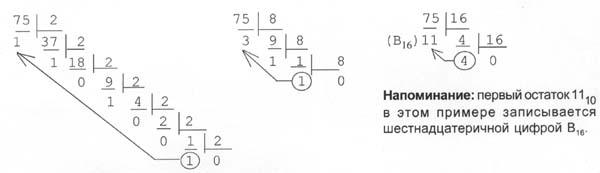
Ответ: 75₁₀ = 1 001 011₂   =  113₈  =  4B₁₆.

7. Как пеpевести пpавильную десятичную дpобь в любую другую позиционную систему счисления?

Для перевода правильной десятичной дpоби  F  в систему счисления с основанием  q  необходимо  F  умножить на  q , записанное в той же десятичной системе, затем дробную часть полученного произведения снова умножить на  q, и т. д., до тех пор, пока дpобная часть очередного пpоизведения не станет pавной нулю, либо не будет достигнута требуемая точность изображения числа F   в q-ичной системе. Представлением дробной части числа F   в новой системе счисления будет последовательность целых частей полученных произведений, записанных в порядке их получения и изображенных одной q-ичной цифрой. Если требуемая точность перевода числа F  составляет k  знаков после запятой, то предельная абсолютная погрешность при этом равняется q -(k+1) / 2.

Пример. Переведем число 0,36 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

Для чисел, имеющих как целую, так и дробную части, перевод из десятичной системы счисления в другую осуществляется отдельно для целой и дробной частей по правилам, указанным выше.