Теоретический материал Что такое система счисления
 Скачать 202.83 Kb. Скачать 202.83 Kb.
|
|
Теоретический материал 1. Что такое система счисления?
Существуют позиционные и непозиционные системы счисления. В непозиционных системах счисления вес цифры (т. е. тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа. Так, в римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен просто десяти. В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Например, в числе 757,7 первая семерка означает 7 сотен, вторая — 7 единиц, а третья — 7 десятых долей единицы. Сама же запись числа 757,7 означает сокращенную запись выражения 700 + 50 + 7 + 0,7 = 7 . 102 + 5 . 101 + 7 . 100 + 7 . 10-1 = 757,7. Любая позиционная система счисления характеризуется своим основанием.
За основание системы можно принять любое натуральное число — два, три, четыре и т.д. Следовательно, возможно бесчисленное множество позиционных систем: двоичная, троичная, четверичная и т.д. Запись чисел в каждой из систем счисления с основанием q означает сокращенную запись выражения an-1 qn-1 + an-2 qn-2 + ... + a1 q1 + a0 q0 + a-1 q-1 + ... + a-m q-m, где ai — цифры системы счисления; n и m — число целых и дробных разрядов, соответственно. Например: 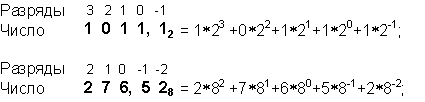 2. Как порождаются целые числа в позиционных системах счисления?В каждой системе счисления цифры упорядочены в соответствии с их значениями: 1 больше 0, 2 больше 1 и т.д.
Продвинуть цифру 1 значит заменить её на 2, продвинуть цифру 2 значит заменить её на 3 и т.д. Продвижение старшей цифры (например, цифры 9 в десятичной системе) означает замену её на 0. В двоичной системе, использующей только две цифры — 0 и 1, продвижение 0 означает замену его на 1, а продвижение 1 — замену её на 0. Целые числа в любой системе счисления порождаются с помощью Правила счета [44]:
Применяя это правило, запишем первые десять целых чисел в двоичной системе: 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001; в троичной системе: 0, 1, 2, 10, 11, 12, 20, 21, 22, 100; в пятеричной системе: 0, 1, 2, 3, 4, 10, 11, 12, 13, 14; в восьмеричной системе: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11. 3. Какие системы счисления используют специалисты для общения с компьютером? Кроме десятичной широко используются системы с основанием, являющимся целой степенью числа 2, а именно: двоичная (используются цифры 0, 1); восьмеричная (используются цифры 0, 1, ..., 7); шестнадцатеричная (для первых целых чисел от нуля до девяти используются цифры 0, 1, ..., 9, а для следующих чисел — от десяти до пятнадцати — в качестве цифр используются символы A, B, C, D, E, F). Полезно запомнить запись в этих системах счисления первых двух десятков целых чисел:
Из всех систем счисления особенно проста и поэтому интересна для технической реализации в компьютерах двоичная система счисления. 4. Почему люди пользуются десятичной системой, а компьютеры — двоичной? Люди предпочитают десятичную систему, вероятно, потому, что с древних времен считали по пальцам, а пальцев у людей по десять на руках и ногах. Не всегда и не везде люди пользуются десятичной системой счисления. В Китае, например, долгое время пользовались пятеричной системой счисления.  А компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами: для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т.п.), а не, например, с десятью, — как в десятичной; представление информации посредством только двух состояний надежно и помехоустойчиво; возможно применение аппарата булевой алгебры для выполнения логических преобразований информации; двоичная арифметика намного проще десятичной. Недостаток двоичной системы — быстрый рост числа разрядов, необходимых для записи чисел. |
