курсовая математическая грамотность. Теоритические аспекты формирования математической грамотности у учеников
 Скачать 150.22 Kb. Скачать 150.22 Kb.
|
|
Содержание Введение………………………………………………………………………..….3 ГЛАВА 1. Теоритические аспекты формирования математической грамотности у учеников…………………………………………………………..6 1.1 Понятие «математическая грамотность»…………………………….…...6 1.2 Основные подходы к оценке математической грамотности школьников………………………………………………………………………..8 ГЛАВА 2. Оценка математической грамотности школьников РФ……………14 2.1 Оценка математической грамотности школьников РФ в соответствии с требованиями ФГОС……………………………………………………………..14 2.2 Основные результаты изучения математической грамотности в исследованиях PISA……………………………………………………………..18 Глава 3. Формирование математической грамотности на уроках математики, как ключевое направление развития математического образования в РФ……23 Заключение……………………………………………………………………….28 Список источников………………………………………………………………31 Введение Современное общество меняет взгляд на содержание математического образования. Основное внимание направлено на развитие способности учащихся применять полученные в школе знания и умения в жизненных ситуациях. В международных исследованиях PISA (Programme for International Student Assessment) математическая грамотность определяется как «способность человека определять и понимать роль математики в мире, в котором он живет, высказывать хорошо обоснованные математические суждения и использовать математику так, чтобы удовлетворять в настоящем и будущем потребности, присущие созидательному, заинтересованному и мыслящему гражданину». В исследованиях проверяется способность 15-летних учащихся использовать математические знания в ситуациях близких к реальным, связанных с разнообразными аспектами окружающей действительности: жизни школы, общества, личной жизни учащихся и т.д. Невысокие результаты наших школьников во всех трех циклах исследования (2013 г., 2016 г., 2018 г.) вызвали широкую дискуссию в обществе о качестве российского образования, приоритетах в содержании математического образования. Многие ученые и школьные учителя видят выход из создавшейся ситуации в реализации компетентностного подхода при обучении математике учащихся основной школы. Данный подход не отрицает значения знаний, но акцентирует внимание на способности использовать полученные знания в жизни. При таком подходе цели образования описываются в терминах, отражающих новые возможности обучаемых, рост их личного потенциала. Объектом исследования математическая грамотность учеников в российских школах. Предметом исследования служат компетентностно-ориентированные задачи в этом процессе. Цель работы состоит в выявлении направлений развития математической грамотности учеников, как ключевом направлении развития российского образования в сфере математики. В основу работы положена гипотеза : если на уроках математики и внеклассных занятиях в основной школе систематически использовать компетентностно-ориентированные задачи в соответствии с разработанными методическими рекомендациями, то повысится математическая грамотность учащихся. Для достижения поставленной цели и проверки сформулированной гипотезы потребовалось решить следующие задачи : 1. Рассмотреть понятие математической грамотности с точки зрения разработчиков международных исследований PISA. 2. Определить основные подходы к оценке математической грамотности школьников 3. Провести оценку математической грамотности школьников РФ в соответствии с требованиями ФГОСТ 4. Проанализировать основные результаты изучения математической грамотности в исследованиях PISA 5. Рассмотреть формирование математической грамотности на уроках математики, как ключевое направление развития математического образования в РФ. Для решения задач использованы следующие методы : 1. Изучение методической литературы по данной теме; 2. Изучение опыта работы преподавателей; 3. Анализ упражнений из школьных учебников по математике; 4. Анализ международных исследований в области математической грамотности; 5. Опытное преподавание. Теоретическая значимость работы состоит в разработке методических рекомендаций для составления и использования компетентностно-ориентированных задач на уроках математики в основной школе. Практическая значимость работы состоит в возможности использования студентами и преподавателями разработанных материалов при подготовке к урокам и факультативным занятиям по математике. Работа состоит из введения, пяти параграфов, заключения, библиографического спис. Глава 1. Теоритические аспекты формирования математической грамотности у учеников
«Математическая грамотность – способность человека определять и понимать роль математики в мире, в котором он живет, высказывать хорошо обоснованные математические суждения и использовать математику так, чтобы удовлетворять в настоящем и будущем потребности, присущие созидательному, заинтересованному и мыслящему гражданину». [5,c.99] В определении «математической грамотности» основной упор сделан не на овладение предметными умениями, а на функциональную грамотность, позволяющую свободно использовать математические знания для удовлетворения различных потребностей – как личных, так и общественных. Согласно этому основное внимание нужно уделять проверке способности учащихся использовать математические знания в разнообразных ситуациях, требующих для своего решения различных подходов, размышлений и интуиции. Очевидно, что для этого явно необходимо иметь значительный объем математических знаний и умений, которые не сводятся к знанию математических фактов, терминологии, стандартных методов и умению выполнять стандартные действия и использовать определенные методы. Сущность понятия «грамотности» определяется тремя признаками:
Необходимо изменить приоритеты в школьном образовании, переориентироваться на компетентностный подход, непрерывное самообразование, овладение новыми информационными технологиями, умение сотрудничать и работать в группах и др. Она оценивается в тестах ВОУД, ЕНТ, в заданиях PISA, TIMSS и других международных исследованиях. Учащиеся должны уметь решать любые поставленные перед ними задачи. В зависимости от сложности задания выделены три уровня математической компетентности: уровень воспроизведения, уровень установления связей, уровень рассуждений. Первый уровень (уровень воспроизведения) — это прямое применение в знакомой ситуации известных фактов, стандартных приемов, распознавание математических объектов и свойств, выполнение стандартных процедур, применение известных алгоритмов и технических навыков, работа со стандартными, знакомыми выражениями и формулами, непосредственное выполнение вычислений. Второй уровень (уровень установления связей) строится на репродуктивной деятельности по решению задач, которые, хотя и не являются типичными, но все же знакомы учащимся или выходят за рамки известного лишь в очень малой степени. Содержание задачи подсказывает, материал какого раздела математики надо использовать и какие известные методы применить. Обычно в этих задачах присутствует больше требований к интерпретации решения, они предполагают установление связей между разными представлениями ситуации, описанной в задаче, или установление связей между данными в условии задач. Третий уровень (уровень рассуждений) строится как развитие предыдущего уровня. Для решения задач этого уровня требуются определенная интуиция, размышления и творчество в выборе математического инструментария, интегрирование знаний из разных разделов курса математики, самостоятельная разработка алгоритма действий. Задания, как правило, включают больше данных, от учащихся часто требуется найти закономерность, провести обобщение и объяснить или обосновать полученные результаты. [8, c.36]
В последнее время меняется взгляд на то, какой должна быть подготовка выпускника основной школы. Наряду с получением предметных знаний и умений, школа должна вырабатывать умения использовать их в разнообразных ситуациях, близких к реальным [5]. Организация Экономического Сотрудничества и Развития (OECD) начала работу по Международной Программе оценки знаний и умений учащихся (PISA), основная цель которой – получение надежных сведений о результатах обучения в различных странах мира, сравнимых на международном уровне. Исследование PISA проводится трехлетними циклами. Дополнительно к оценке учебных достижений изучается отношение учащихся к обучению. По мнению разработчиков, полученная информация позволит странам-участницам принимать обоснованные решения в области образования. Особый интерес вызывает возможность определить состояние тех знаний и умений, которые могут быть полезны ребятам в будущем, а также умения самостоятельно приобретать знания, необходимые для успешной адаптации в современном мире. Исследование проводится среди учащихся 15-летнего возраста. Ключевой вопрос исследования – «Обладают ли учащиеся 15-летнего возраста, получившие общее обязательное образование, знаниями и умениями, необходимыми для полноценного функционирования в обществе?» (15, с. 5). Исследование направлено не на определение уровня освоения школьных программ, а на оценку способности, учащихся применять полученные знания и умения в жизненных ситуациях. Такой выбор объясняется тем, что во многих странах к этому возрасту завершается обязательное обучение в школе и программы обучения в разных странах имеют много общего. Именно на этом этапе образования важно определить состояние тех знаний и умений, которые могут быть полезны школьникам в будущем, а также способности самостоятельно приобретать знания, необходимые для успешной адаптации в современном мире. Проверке овладения конкретным содержанием учебных дисциплин не уделяется много времени. Основное время отводится изучению состояния более широких знаний и умений, необходимых во взрослой жизни и приобретенных при изучении школьных предметов, а также оценке межпредметной компетентности учащихся (использованию знаний, полученных в рамках изучения различных предметов или из других источников информации, для решения поставленной задачи). В каждом цикле исследования оценивается функциональная грамотность учащихся в области чтения, математики, естествознания. В 2015 году приоритетной областью исследования была грамотность чтения, в 2016 – естественнонаучной грамотности, в 2017 году - математическая грамотность. В исследованиях PISA-2016 проверка математической подготовки учащихся основана на понятии «математическая грамотность», которое определяется как «способность человека определять и понимать роль математики в мире, в котором он живет, высказывать хорошо обоснованные математические суждения и использовать математику так, чтобы удовлетворять в настоящем и будущем потребности, присущие созидательному, заинтересованному и мыслящему гражданину» [15, с.7]. Содержание этого понятия уточняется следующим образом: «под математической грамотностью понимается способность учащихся:
В исследованиях PISA основное внимание было уделено проверке способностей учащихся использовать математические знания в ситуациях близких к реальным, связанных с разнообразными аспектами окружающей действительности: жизни школы, общества, личной жизни учащихся и т.д. Для решения поставленных проблем учащимся необходимо иметь значительный объем математических знаний и умений, которые обычно формируются в школе. В исследовании не ставится цель проверить каждое из выделенных предметных знаний и умений в отдельности. В большинстве ситуаций требуется использовать знания и умения из разных тем и разделов не только курса математики, но и других школьных предметов, например, физики, биологии, химии. Необходимо также такое важнейшее общеучебное умение, как умение внимательно прочитать некоторый связный текст, выделить в приведенной в нем информации только те факты и данные, которые необходимы для получения ответа на поставленный вопрос. В соответствии с замыслом авторов концепции исследования каждое задание соответствует одной из четырех содержательных областей: 1. Пространство и форма — это вопросы, относящиеся к пространственным и плоским геометрическим формам и отношениям, которые часто встречаются в школьных программах по геометрии разных стран. Они связаны с поиском сходства в различия при анализе фигур и их частей, распознаванием фигур в различных конфигурациях и с разными размерами, а также пониманием свойств объектов и их взаимного расположения. 2. Изменение и отношения – вопросы, связанные с математическим описанием различных процессов, таких как зависимости между переменными, в том числе функциональные. В большей степени этот материал относится к алгебре. Математические отношения, рассматриваемые в заданиях, могут выражаться уравнениями или неравенствами, но используются также и отношения более общей природы (например, эквивалентность, делимость, включение). Отношения задаются разными способами, включая символические, алгебраические, графические, табличные и геометрические. 3. Количество — эта область включает вопросы, связанные с числами. В программах по математике этот материал чаще всего относится к арифметике. При выполнении заданий от учащихся требуется умение выполнять сравнение чисел и величин, распознавать числовые выражения и формулы, использовать числа для представления количественных характеристик реальных объектов (подсчеты и измерения). Кроме того, эта область связана с пониманием разных форм представления чисел и выполнением действий с числами, представленными в разных формах. Важным аспектом в соответствующих задачах являются также рассуждения, связанные с числами и проявляющиеся во владении разными представлениями чисел, а также в понимании смысла операций, устных вычислений и приближенных оценок. 4. Неопределенность — включает в себя вероятностные и статистические явления и зависимости, которые имеют самое непосредственное отношение к современному информационному обществу. Эти явления и зависимости являются предметом изучения разделов статистики и вероятности. В исследовании подчеркивается, что в совокупности эти четыре содержательные области покрывают диапазон математических знаний, необходимых 15-летним учащимся в качестве основы для жизни и для дальнейшего расширения их математического кругозора. Следует отметить, что содержание заданий, предлагаемых в тестах, связано с материалом традиционных разделов или тем, составляющих основу программ обучения в большинстве стран мира, в том числе и в России: числа, алгебра, функции, геометрия, вероятность, статистика, дискретная математика (к ней отнесены комбинаторные задачи и задания на поиск закономерности в парах чисел, в числовых последовательностях и последовательностях геометрических фигур). По сравнению с более традиционным тематическим подходом концентрация содержания проверки вокруг четырех содержательных областей (обобщающих идей) позволяет более широко охарактеризовать результаты, показанные учащимися, с позиций овладения идеями, тесно связанными с особенностями (сущностью) реальных явлений окружающего мира. Уровень овладения этими идеями позволяет более адресно оценить возможности учащихся в использовании полученных знаний в повседневной жизни (личной и общественной), что и является целью исследования PISA. На международном уровне для грамотного современного человека считаются необходимыми следующие математически знания и умения: пространственные представления; пространственное воображение; свойства пространственных фигур; умение читать и интерпретировать количественную информацию, представленную в различной форме (таблиц, диаграмм, графиков реальных зависимостей); знаковые и числовые последовательности; определение периметра и площадей нестандартных фигур; действия с процентами; использование масштаба; использование статистических показателей для характеристики различных реальных явлений и процессов; умение выполнять действия с различными единицами измерения (длины, массы, времени, скорости) и др. На основании вышесказанного можно сделать вывод, что концепция оценки математической грамотности включает теоретические обоснования оценки математической подготовки учащихся: определение математической грамотности, описание познавательной деятельности учащихся при применении математической грамотности и фундаментальных математических способностей, которые лежат в основе этой деятельности. В концепции описан подход к организации содержания проверки – распределение его на четыре области. Эти области охватывают математическое содержание, которое составляет базу для обеспечения успешного функционирования в современном обществе. Описываются четыре контекстных категории, в рамках которых учащимся будут предложены математические проблемы. Установлены соотношения между количеством заданий по четырем содержательным областям и контекстным категориям, которые обеспечивают получение достоверной информации о подготовке учащихся по каждой из областей и категорий контекста. ГЛАВА 2. Оценка математической грамотности школьников РФ 2.1 Оценка математической грамотности школьников РФ в соответствии с требованиями ФГОС4 В рамках развития математической грамотности у школьников, в 2017 году была проведена оценка математической грамотности школьников РФ. Проанализируем полученные результаты. «Работа с текстовыми задачами»: у примерно 60% учащихся сформированы навыки проведения анализа задачи, установления зависимости между величинами, определения количества и порядка действий для решения задачи, выбора и объяснения выбора действий, а также метода решения арифметическим способом: либо по действиям, либо составлением числового выражения. «Работа с информацией»: около половины учащихся верно интерпретировали информацию, полученную при проведении несложных исследований данных, представленных таблично. «Пространственные отношения. Геометрические фигуры»: две трети учащихся правильно распознали геометрические фигуры в пространстве и соотнесли их с реальными предметами окружающей действительности. 3) Четверть учащихся не умеет устанавливать взаимосвязь между условием и вопросом задачи, оценивать правильность хода решения и реальность ответа на вопрос задачи, а также понимать смысл доли; треть учащихся не смогла вычислить периметр нестандартной прямоугольной и квадратной фигур. 4) Требует корректировки методика изучения и оценки знаний учащихся теоретических положений и отработки базовых конструкций по теме «Работа с текстовыми задачами», а также включение предметного содержания не в типичные учебные математические задачи, близкие к реальным проблемным ситуациям, связанным с разнообразными аспектами жизни учащихся (личной жизнью, жизнью школы или общества, профессиональной деятельностью, наукой) и требующих для своего решения большей или меньшей математизации. 5) Типичные ошибки и недочёты: вычислительные ошибки; несформированность умений выполнять устные и письменные действия с натуральными числами; неумение проводить проверку правильности вычислений (с помощью обратного действия, прикидки и оценки результата действия); неумение переходить от словесной формы записи условия к аналитической и наоборот; недостаточная отработка использования приобретённых знаний и умений при решении геометрических задач; нетвердое владение арифметическим способом решения текстовых задач; недостаточное владение методом математического моделирования, в частности, неумение переформулировать и моделировать условие, выбирать различные методы арифметического способа решения задач, интерпретировать результат, применять различные формы самоконтроля. 6) Выбор учащимися соответствующих заданий и результаты их выполнения по содержательным областям: «Пространство и форма» - это вопросы (№ 6 и № 12), относящиеся к пространственным и плоским геометрическим формам и отношениям, т.е. к геометрическому материалу: из 95,8% учащихся, выбравших соответствующие задания, 51,1% выполнили их верно. «Изменение и зависимости» - вопросы (№ 4), связанные с математическим описанием зависимости между переменными в различных процессах, т.е. с алгебраическим материалом: 30,0% учащихся из 93,7%, приступивших к выполнению, справилось с подобным заданием. «Количество» - эта область включает вопросы (№ 1-3, № 7-11), связанные с числами и величинами, т.е. относится к арифметике: только 60,2% учащихся из 97,9%, решавших данные задания, владеют вычислительной техникой и математическим аппаратом решения текстовых задач с реальным сюжетом. «Неопределённость» - включает статистические явления и зависимости (№ 5), которые имеют непосредственное отношение к современному информационному обществу: у 58,4% учащихся из 95,4%, выбравших эти задания, сформированы соответствующие навыки. 7) Наибольшие трудности у учащихся вызвали задания из реальной математики: практически каждый второй пятиклассник не умеет решать задачи с геометрическим контекстом и текстовые задачи из реальной практики, что является необходимым условием положительной аттестации выпускников на ГИА в форме ОГЭ. 8) Распределение учащихся по группам сформированности математических компетенций: в группе компетенций «воспроизведение»: 71% учащихся применяет знакомые математические объекты, свойства, факты, алгоритмы, приёмы в стандартных, знакомых ситуациях; в группе компетенций «установление связей»: 58% учащихся продемонстрировали способность к интеграции и установление связей между материалом, относящимся к различным содержательным областям или тематическим разделам программы, а также между разными формами представления информации в описанной жизненной ситуации; в группе компетенций «рассуждения»: 31% учащихся показал умения составлять план стратегии решения и применять его для решения комплексной проблемной ситуации, а также умения проводить обоснованные рассуждения и объяснения полученных результатов. 9) Характеристика сформированности общих учебных умений, навыков и способов деятельности учащихся: Познавательная деятельность: 61% учащихся использует для познания окружающего мира различные методы (наблюдение, измерение, опыт, моделирование и др.), выделяет значимые функциональные связи и отношения между частями целого, умеет сравнивать, сопоставлять, ранжировать объекты по критериям, разделять процессы на этапы, исследует несложные практические ситуации. Информационно-коммуникативная деятельность: 58% тестируемых осознанно бегло читают тексты заданий, проводят информационно-смысловой анализ текста, создают письменные высказывания, составляют план решения, подбирают аргументы, формулируют выводы, умеют перефразировать мысль (объяснять «иными словами»), выбирать и использовать выразительные средства языка и знаковых систем (текст, таблица, схема, и др.) в соответствии с коммуникативной задачей. Рефлексивная деятельность: 73% пятиклассников самостоятельно организуют собственную учебную деятельность (постановка цели, планирование, определение оптимального соотношения цели и средств и др.), владеют навыками контроля своей деятельности, умением предвидеть возможные последствия своих действий, осуществляют поиск и устраняют причины возникших трудностей, оценивают свои учебные достижения. По результатам исследования учащиеся распределились по трем уровням математической грамотности: I уровень (высокий) – 35% учащихся, показавшие высокий уровень достижения планируемых результатов, могут создавать и работать с моделями сложных проблемных ситуаций, распознавать их ограничения и устанавливать соответствующие допущения; могут выбирать, сравнивать, оценивать соответствующие стратегии решения, могут размышлять и рассуждать, устанавливать связи из извлекаемой информации, описывать её на различных языках, формулировать и излагать свою интерпретацию и рассуждения. II уровень (средний) – 45% учащихся, показавшие базовый и повышенный уровни достижения планируемых результатов, способны выполнять чётко описанные процедуры, которые требуют принятия решения на каждом последующем шаге, могут кратко описать свою интерпретацию, аргументацию и результаты, но не всегда могут интегрировать информацию и связывать её напрямую с различными аспектами реальной ситуации, не всегда продуктивно рассуждают. III уровень (низкий) - 20% учащихся, показавшие низкий и пониженный уровни достижения планируемых результатов, не способны отвечать на вопросы в знакомой ситуации, выполнять стандартные процедуры, извлекать соответствующую информацию, не могут выполнять действия, которые явно следуют из описания предложенной ситуации, осуществлять самоконтроль своей деятельности. Результаты мониторинга показывают, что у большинства учащихся, принимавших участие в исследовании, математическая грамотность сформирована на уровне, достаточном для продолжения обучения в основной школе. Однако данное исследование следует считать пилотным. Для получения более объективных результатов его необходимо продолжить. 2.2 Основные результаты изучения математической грамотности в исследованиях PISA Во всех трех циклах PISA российские школьники показали невысокий уровень математической грамотности. В качестве основной количественной характеристики математической подготовки учащихся конкретной страны используется средний балл, подсчитанный по результатам выполнения математической части работы учащимися этой страны. Среди стран-участниц исследований PISA Россия в 2014 году занимала 21 место из 32 стран, в 2013 году – 29 место из 40, в 2016 году – 34 место из 57. Результаты международного исследования PISA-2014вызвали широкую дискуссию в обществе о качестве российского математического образования, приоритетах в содержании общего среднего образования, способствовавшую появлению новых направлений исследований, прежде всего, - в области изучения целесообразности и возможности реализации так называемого компетентностного подхода в образовании. В 2012 году распоряжением Правительства Российской Федерации была принята Концепция модернизации Российского образования до 2020 года. В соответствии с Концепцией общеобразовательная школа призвана формировать «новую систему универсальных знаний, умений, навыков, а также опыт самостоятельной деятельности и личной ответственности обучающихся, то есть современные ключевые компетентности» [16]. Определенные таким образом цели образования ориентируют на компетентностный подход к организации образовательного процесса [22]. Однако, итоги исследований PISA -2013 и PISA -2016 показали, что результаты российских школьников по сравнению со сверстниками других стран (близких к России вPISA -2014), не только не улучшились, но и ухудшились. В таблице 1 приведены итоги исследований в тех странах, результат которых практически не отличался от результата российских школьников в исследовании PISA-2014. Таблица 1 Средние результаты пяти стран по математической грамотности
Из таблицы видно, что результаты всех стран, которые не отличались от результатов России в начале исследования, значительно улучшились в последующем. Чего нельзя сказать о результатах российских школьников. Результаты исследования математической грамотности не только не улучшились, а наоборот ухудшились. Сравнение результатов России с другими странами показывает отличие приоритетов отечественного математического образования от приоритетов, которые проявились в международных исследованиях. Пятнадцатилетние российские учащиеся в этих исследованиях явно продемонстрировали, что они затрудняются в решении задач, в которых представлены ситуации, близкие к реальным. Это свидельствует о том, что заявленная в школьной программе необходимость прикладной и практической ориентации на практике не реализуется [6]. Школьные учителя объясняют такое положение дел тем, что для реализации компетентностного подхода с целью повышения математической грамотности учащихся недостаточно разработано методическое обеспечение процесса обучения математике в основной школе. Анализ результатов международных проверок позволил выявить характерные недочеты математической подготовки российских школьников. К ним относятся недостаточное усвоение ряда тем, имеющих широкое практическое применение: отношение чисел, пропорциональные величины, решение задач на проценты, определение периметров и площадей фигур, оценка и прикидка результатов, чтение графиков реальных зависимостей. Результаты исследований позволяют определить направления совершенствования содержания математического образования в школах России. По мнению Г.С.Ковалевой «прежде всего, уже с начальной школы следует изучать тему «Анализ данных. Вероятность. Статистика», овладение которой способствует адаптации учащихся в обществе. Необходимо уменьшить внимание к формированию аппаратных умений и усилить роль знаний, имеющих важное практическое значение. В курсе математики 5-6 классов следует уделить большое внимание наглядной геометрии и вопросам прикладного характера (оценке и прикидке результатов, анализу количественных данных, представленных в различной форме; процентным расчетам; пропорциональным величинам). В курсе 7-9 классов эти направления должны получить дальнейшее развитие. Необходимо увеличить количество заданий практического содержания, связанных с описанием реальных ситуаций»[7]. В последнее время меняется взгляд на то, какой должна быть подготовка выпускника основной школы по математике. В международных исследованиях PISAпод математической грамотностью понимается «способность человека определять и понимать роль математики в мире, в котором он живет, высказывать хорошо обоснованные математические суждения и использовать математику так, чтобы удовлетворять в настоящем и будущем потребности, присущие созидательному, заинтересованному и мыслящему гражданину». На международном уровне для грамотного современного человека считаются необходимыми следующие математически знания и умения: пространственные представления; пространственное воображение; свойства пространственных фигур; умение читать и интерпретировать количественную информацию, представленную в различной форме (таблиц, диаграмм, графиков реальных зависимостей); знаковые и числовые последовательности; определение периметра и площадей нестандартных фигур; действия с процентами; использование масштаба; использование статистических показателей для характеристики различных реальных явлений и процессов; умение выполнять действия с различными единицами измерения (длины, массы, времени, скорости) и др. Во всех трех исследованиях PISA российские школьники показали невысокий уровень математической грамотности. Итоги международного исследования PISAвызвали широкую дискуссию в обществе о качестве российского математического образования. В 2001 году распоряжением Правительства Российской Федерации была принята Концепция модернизации Российского образования до 2010 года. В этом документе общеобразовательная школа призвана формировать «новую систему универсальных знаний, умений, навыков, а также опыт самостоятельной деятельности и личной ответственности обучающихся, то есть современные ключевые компетентности». Такие же цели и задачи сформулированы в концепции математического образования. Определенные таким образом цели образования ориентируют на компетентностный подход к организации образовательного процесса, предполагают смену требований к критериям оценки результатах обучения. Однако, итоги исследований PISA -2013 и PISA -2016 показали, что результаты российских школьников по сравнению со сверстниками других стран (близких к России вPISA -2014), не только не улучшились, но и ухудшились. Школьные учителя объясняют такое положение дел тем, что для реализации компетентностного подхода с целью повышения математической грамотности учащихся недостаточно разработано методическое обеспечение процесса обучения математике в основной школе. Глава 3. Формирование математической грамотности на уроках математики, как ключевое направление развития математического образования в РФ Проблема формирования функциональной грамотности требует изменений к содержанию деятельности на уроке. Научиться действовать ученик может только в процессе самого действия, а ежедневная работа учителя на уроке, образовательные технологии, которые он выбирает, формируют функциональную грамотность учащихся.. Ученики должны активно принимать участие на всех этапах учебного процесса: формулировать свои собственные гипотезы и вопросы, консультировать друг друга, ставить цели для себя, отслеживать полученные результаты. Прочное усвоение материала достигается посредством учебного процесса, в центре которого находится ученик, поэтому на протяжении всех уроков необходимо:
Развитие человека происходит в тесной взаимосвязи когнитивного, социального и эмоционального мышления. Одной из составляющих такого развития является диалоговое обучение. Диалоговое обучение взаимосвязано с обучением критическому мышлению. Использование технологии критического мышления очень эффективно на уроках математики. Оно развивает умение работать с информацией, логически мыслить, решать проблемы, аргументировать свое мнение, самообучаться, сотрудничать и работать в группе. Ученикам очень нравится составлять кластер по разным темам, задание на возращение к «известной информации», прием «мозайка, инструкции, памятки», вопросы верно или не верно, прием «корзина идеи» для отработки навыка решения задач. Учитель и ученик меняются ролями, главная роль принадлежит ученику, а учитель — консультант, помощник. В планировании последующих действий учителя по составлению плана работы по повышению качества усвоения учащимися учебного материала большое значение имеет оценивание, самопроверка и взаимопроверка дают большие возможности, учащиеся начинают ощущать себя активными участниками процесса своего обучения, учатся защищать свою работу. Их надо учить анализировать свою работу, решать, что нужно сделать для улучшения усвоения материала, как преодолеть проблемы, контролировать процесс продвижения к цели, самооценка в большой степени связана с саморегулированием. Развивать математическую грамотность надо постепенно, начиная с 5 класса. Регулярно включать в ход урока задания на «изменение и зависимости», «пространство и форма», «неопределенность», «количественные рассуждения» и т.п.. Эти задания можно использовать по усмотрению учителя:
Для выполнения заданий требуется относительно небольшой объем знаний и умений, которые необходимы для математически грамотного современного человека. К ним отнесены:
Можно применять полученные знания и умения на уроках к решению проблем, возникающих в повседневной практике Например в тестах Пиза даны задания ОКРУГЛЕНИЕ(5 кл) Алисе необходимо найти сумму чисел 19,6,23,8 и 38,4, округлив их до ближайшего целого числа. Какие три числа ей взять? ЖИЛОЙ ДОМ На фотографии виден жилой дом, у которого крыша имеет форму пирамиды. вычислите площадь пола чердака. (Мы можем решить задачу с помощью темы геометрии в 10 классе площадь пирамиды) 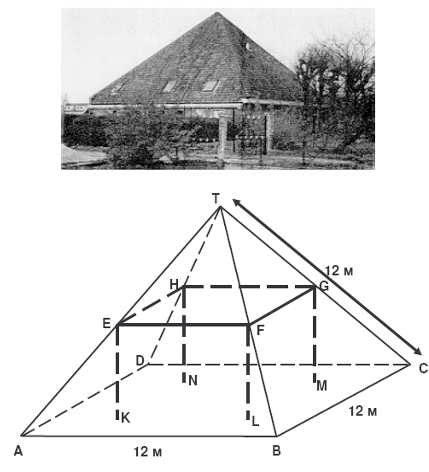 Рисунок 1-Пример задание на расширение математической грамотности Фермер на садовом участке высаживает яблони в форме квадрата, как показано на рисунке. Для защиты яблонь от ветра он сажает по краям участка хвойные деревья. Ниже на рисунке изображены схемы посадки яблонь и хвойных деревьев для нескольких значений n, где n – количество рядов высаженных яблонь. Эту последовательность можно продолжить для любого числа n. 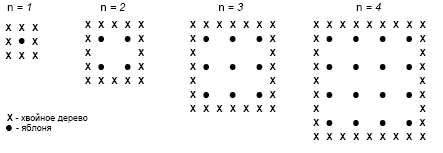 Вопрос 1: Заполните таблицу: 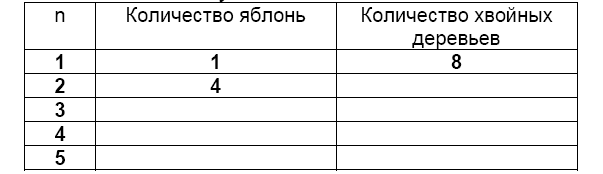 Вопрос 2: В рассмотренной выше последовательности количество посаженных яблонь и хвойных деревьев подсчитывается следующим образом: количество яблонь = n2, количество хвойных деревьев = 8n, где n – число рядов высаженных яблонь. Для какого значения n число яблонь будет равно числу посаженных вокруг них хвойных деревьев? Запишите решение. Вопрос 3: Предположим, что фермер решил постепенно увеличивать число рядов яблонь на своем участке. Что при этом будет увеличиваться быстрее: количество высаживаемых яблонь или количество хвойных деревьев? Заключение Математика занимает особое место в науке, культуре и общественной жизни, являясь одной из важнейших составляющих мирового научно-технического прогресса. Изучение математики играет системообразующую роль в образовании, развивая познавательные способности человека, в том числе к логическому мышлению, влияя на преподавание других дисциплин. Качественное математическое образование необходимо каждому для его успешной жизни в современном обществе. Успех нашей страны в XXI веке, эффективность использования природных ресурсов, развитие экономики, обороноспособность, создание современных технологий зависят от уровня математической науки, математического образования и математической грамотности всего населения, от эффективного использования современных математических методов. Без высокого уровня математического образования невозможны выполнение поставленной задачи по созданию инновационной экономики, реализация долгосрочных целей и задач социально-экономического развития Российской Федерации. Повышение уровня математической образованности сделает более полноценной жизнь россиян в современном обществе, обеспечит потребности в квалифицированных специалистах для наукоемкого и высокотехнологичного производства. Под математической грамотностью понимается способность высказывать обоснованные математические суждения и использовать математические средства для решения практических, исследовательских и познавательных проблем. Выпускник школы стоит сегодня перед проблемой прохождения Государственной итоговой аттестации в основной и старшей школе и ему необходимы соответствующие умения в математической сфере такие как: владение основными алгоритмами; знание и понимание ключевых элементов содержания (математических понятий, ихсвойств, приёмов решения задач и прочее); умение пользоваться математической записью, применять знания к решению математических задач, не сводящихся к прямому применению алгоритма, а также применять математические знания в простейших практических ситуациях; проверка владения материалом на повышенном уровне, предполагающая свободное владение материалом курса и хороший уровень математической культуры. В целях повышения уровня математической грамотности учителям основной школы рекомендуется: 1) практиковать тренинги по отработке техники преобразований, построений, измерений и вычислений, в том числе с использованием электронных образовательных ресурсов; 2) спланировать систему заданий по отработке умений построения и исследования математических моделей задач с практико-ориентированным контекстом; 3) предусмотреть возможность выбора и апробации УМК по математике в основной школе, соответствующих уровню реализуемых в начальной школе программ, уровню подготовки учащихся и требованиям ФГОС ООО; 4) увеличить долю комплексных заданий, заданий комбинированного характера, а также с нестандартными формулировками, дополнительными условиями, на использование нескольких приёмов при решении и отборе решений; «сюжетных» задач; задач на отработку базовых конструкций и включения их в систему более сложных заданий; контекстных задач. Целенаправленное формирование умений решать задачи вообще, математические в частности, является, безусловно, одним из важнейших путей усовершенствования образования. А это, в свою очередь, связано с формированием навыков анализа условия задачи, поиска путей её решения, осмысления результатов решения. Формирование определенной системы математических знаний всегда было в центре внимания в математическом образовании. Объем этой системы является слишком большим с общеобразовательных позиций, а качество владения ими – недостаточно высоким. А главное, формирование этой системы знаний и умений не связана органически с формированием умений применять математику и стратегией решения задач. Успешное выполнение контекстных заданий может быть обеспечено только при ориентации учебного процесса на решение подобных задач. Чтобы повысить математическую грамотность учащихся, можно предложить учащимся самим составить задачи и уравнения, ребусы, кроссоворды, разноуровневые задания. Список используемых источников
|
