|
|
Теория игр. Поиск выигрышной стратегии|
© К. Поляков, 2021
19-21 (19 – базовый уровень, 20 – повышенный уровень,
21 – высокий уровень, время – 6 + 8 + 11 мин)
Тема: Теория игр. Поиск выигрышной стратегии.
Что проверяется:
Умение анализировать алгоритм логической игры. Умение найти выигрышную стратегию игры. Умение построить дерево игры по заданному алгоритму и найти выигрышную стратегию.
1.5.2. Цепочки (конечные последовательности), деревья, списки, графы, матрицы (массивы), псевдослучайные последовательности.
1.1.3. Умение строить информационные модели объектов, систем и процессов в виде алгоритмов.
Что нужно знать:
в простых играх можно найти выигрышную стратегию, просто перебрав все возможные варианты ходов соперников
для примера рассмотрим такую игру: сначала в кучке лежит 5 спичек; два игрока убирают спички по очереди, причем за 1 ход можно убрать 1 или 2 спички; выигрывает тот, кто оставит в кучке 1 спичку
первый игрок может убрать одну спичку (в этом случае их останется 4), или сразу 2 (останется 3), эти два варианта можно показать на схеме:
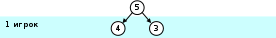
если первый игрок оставил 4 спички, второй может своим ходом оставить 3 или 2; а если после первого хода осталось 3 спички, второй игрок может выиграть, взяв две спички и оставив одну:
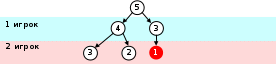
если осталось 3 или 2 спички, то 1-ый игрок (в обеих ситуациях) выиграет своим ходом:
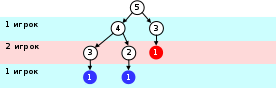
простроенная схема называется «деревом игры», она показывает все возможные варианты, начиная с некоторого начального положения (для того, чтобы не загромождать схему, мы не рисовали другие варианты, если из какого-то положения есть выигрышный ход)
в любой ситуации у игрока есть два возможных хода, поэтому от каждого узла этого дерева отходят две «ветки», такое дерево называется двоичным (если из каждого положения есть три варианта продолжения, дерево будет троичным)
проанализируем эту схему; если первый игрок своим первым ходом взял две спички, то второй сразу выигрывает; если же он взял одну спичку, то своим вторым ходом он может выиграть, независимо от хода второго игрока
кто же выиграет при правильной игре? для этого нужно ответить на вопросы: 1) «Может ли первый игрок выиграть, независимо от действий второго?», и 2) «Может ли второй игрок выиграть, независимо от действий первого?»
ответ на первый вопрос – «да»; действительно, убрав всего одну спичку первым ходом, 1-ый игрок всегда может выиграть на следующем ходу
ответ на второй вопрос – «нет», потому что если первый игрок сначала убрал одну спичку, второй всегда проиграет, если первый не ошибется
таким образом, при правильной игре выиграет первый игрок; для этого ему достаточно первым ходом убрать всего одну спичку
в некоторых играх, например, в рэндзю (крестики-нолики на бесконечном поле) нет выигрышной стратегии, то есть, при абсолютно правильной игре обоих противников игра бесконечна (или заканчивается ничьей); кто-то может выиграть только тогда, когда его соперник по невнимательности сделает ошибку
полный перебор вариантов реально выполнить только для очень простых игр; например, в шахматах сделать это за приемлемое время не удается (дерево игры очень сильно разветвляется, порождая огромное количество вариантов)
все позиции в простых играх делятся на выигрышные и проигрышные
выигрышная позиция – это такая позиция, в которой игрок, делающий первый ход, может гарантированно выиграть при любой игре соперника, если не сделает ошибку; при этом говорят, что у него есть выигрышная стратегия – алгоритм выбора очередного хода, позволяющий ему выиграть
если игрок начинает играть в проигрышной позиции, он обязательно проиграет, если ошибку не сделает его соперник; в этом случае говорят, что у него нет выигрышной стратегии; таким образом, общая стратегия игры состоит в том, чтобы своим ходом создать проигрышную позицию для соперника
выигрышные и проигрышные позиции можно охарактеризовать так:
позиция, из которой все возможные ходы ведут в выигрышные позиции – проигрышная;
позиция, из которой хотя бы один из возможных ходов ведет в проигрышную позицию - выигрышная, при этом стратегия игрока состоит в том, чтобы перевести игру в эту проигрышную (для соперника) позицию.
|
|
|
 Скачать 0.73 Mb.
Скачать 0.73 Mb.