лекции Теория Отраслевых рынков. Теория отраслевых рынков
 Скачать 2.51 Mb. Скачать 2.51 Mb.
|
4. Стратегическое взаимодействие крупных фирм на рынке4.1 Стратегии и модели поведенияВ структуре рынков имеются экономические агенты, которые ориентируются только на свои собственные цели и представления о рынке, а не на поведение других субъектов рынка, это крупные фирмы, преодолевающие ограничения совершенной конкуренции (отсутствие какого-либо значимого влияния на рынок), и совершенной монополии (консерватизм, «задавливание» рынка, неучет действий прочих агентов, включая потенциальных). Ценовое поведение таких агентов выходит за рамки пассивной или активной политики, включая гибкое реагирование цен и объемов выпуска на изменение окружающей экономической среды. Таким образом, рынки, где действуют крупные фирмы, вынуждены считаться с наличием и поведением других контрагентов. Такие рынки являются олигополиями, и поведение фирм является стратегическим. Стратегическое поведение свойственно только рынку олигополии: в условиях свободной конкуренции объем выпуска фирмы не зависит и не влияет на объемы выпуска других фирм. Реализация стратегического поведения фирмы в условиях олигополии происходит в двух основных формах: в виде некооперативного взаимодействия фирм (когда фирмы конкурируют друг с другом и проводят самостоятельную политику на рынке) и в виде кооперативного поведения (когда фирмы предварительно договариваются о совместных действиях и выступают на рынке «единым фронтом»). Некооперативные стратегии поведения классифицируются в зависимости от последовательности принятия решений и выбора фирмами стратегической переменной (объема выпуска или цены). Возможные стратегии представлены в табл.4.1. Таблица 4.1. Стратегии фирм в результате их взаимодействия
Рассмотрим модели стратегического некооперативного взаимодействия крупных фирм. Модель Бертрана Предположим, на рынке действуют две фирмы, производящие однородный продукт. При этом вход на рынок других фирм эффективно закрыт. Целью каждой фирмы является максимизация прибыли. Отсутствуют соглашения фирм друг с другом. Фирмы назначают цены одновременно, так что каждая не может прогнозировать реакцию конкурента на сделанный ею самой выбор. Средние издержки фирм постоянны в долгосрочном периоде и равны между собой. Фирма 1 назначает цену первой. Ее цена может быть любой. Но как только фирма 1 назначила цену, ее цена оказывается фиксированной при принятии решения фирмой 2. Если фирма 2 назначит цену выше цены фирмы 1, она не продаст ничего (спрос переключится на товар той фирмы, которая назначает более низкую цену). Фирма 2 может назначить цену на уровне цены фирмы 1 или ниже. Во втором случае фирма 2 захватывает весь рынок. Подобную стратегию может проводить фирма 1 по отношению к фирме 2. В результате на рынке возникает ценовая конкуренция, и, как следствие, цена падает до минимально возможного уровня. Если фирмы идентичны, и их предельные издержки равны, равновесная цена установится на уровне предельных издержек. Любая цена выше предельных издержек не сможет стабилизировать рынок. Если же предельные издержки фирм не равны, фирма с более низкими предельными издержками получит конкурентное преимущество путем назначения цены ниже того уровня, при котором другая фирма еще сможет осуществлять свою деятельность на рынке. В результате фирма с более высокими издержками вынуждена будет уйти из отрасли. Таким образом, олигопольное взаимодействие в его простейшей форме при равенстве предельных издержек конкурирующих фирм оказывается нестабильным и приводит к ценовой войне, истощающей силы обеих сторон, а следовательно, и к конкурентному результату - нулевой прибыли в долгосрочном периоде, что ликвидирует стимулы крупных фирм к производству и сбыту данного вида товара. Этот результат взаимодействия олигополистов известен как парадокс Бертрана. В рамках теории игр он известен как «дилемма заключенного»: если виновные в совершении преступления стоят перед выбором стратегии «сознаваться» или «не сознаваться», причем делают выбор одновременно и независимо друг от друга, для каждого из них доминирующей стратегией служит стратегия «сознаваться». Рациональный выбор заключенных будет состоять в том, чтобы сознаться, несмотря на возможность улучшения положения обоих в случае выбора ими стратегии «не сознаваться». Если бы парадокс Бертрана имел место в действительности, крупные фирмы перестали бы заниматься производством, и рынок олигополии прекратил бы свое существование. Однако в реальности это не так. Крупные фирмы не только не прекращают производство, но и представляют собой господствующую структуру современной рыночной экономики, получая прибыли в долгосрочном периоде. Более реальными являются его модификации. «Дилемма заключенного» в бесконечно повторяющейся игре Рассмотрим каким образом парадокс Бертрана может быть разрешен в бесконечно повторяющейся игре, используя терминологию теории игр. Если взаимодействие двух фирм продолжается один период времени, то игра приобретает характер «дилеммы заключенного». Возможные комбинации стратегий фирм и получаемых ими выигрышей представлены на рис. 4.1.
Рис. 4.1. Матрица ценовой игры в модели Бертрана Фирмы могут выбирать стратегии низкой или высокой цены и получать соответственно результаты (прибыли) такие, что π2<π1>π4>π3. Отсюда доминирующей стратегией для каждой фирмы будет стратегия «назначать низкую цену». Если их взаимодействие продолжится бесконечно долго доминирующими могут быть только две стратегии:
Максимальный выигрыш каждой фирмы в результате применения первой стратегии с учетом дисконтирования равен: где π1 - прибыль, полученная фирмой, назначающей высокую цену, при условии, что другая фирма также назначает высокую цену; δ- дисконтирующий множитель, связанный со ставкой дисконтирования δ = 1/(1+i), I - ставка дисконтирования; ρ - вероятность в момент времени t того, что фирмы будут взаимодействовать в момент (t+1) - вероятность продолжения игры в будущем. Максимальный выигрыш фирмы от применения второй стратегии равен: где π2- прибыль, полученная фирмой, назначающей низкую цену, при условии, что другая фирма назначает высокую цену; π4 - прибыль, полученная фирмой, назначающей низкую цену, при условии, что другая фирма назначает низкую цену. Выбор оптимальной стратегии фирмы, таким образом, зависит от соотношения значений выигрышей по каждому из возможных вариантов. Если РV(р)1 > РV(р)2, то есть если то стимулов вести ценовую войну у фирм не будет. Выбор стратегии «ценовой войны» или «ценового мира» зависит как от объективных факторов - вероятности продолжения взаимодействия фирм в будущем, так и от субъективных факторов - межвременных предпочтений фирм. Модель Бертрана с дифференцированным продуктом Стандартная модель Бертрана предполагает совершенную заменимость товаров двух фирм. Однако они могут производить и разнородную (дифференцированную) продукцию. Предположим спрос на товар каждой фирмы описывается уравнением: где Рj - цена, назначаемая данной фирмой; Рj - цена фирмы-конкурента (i,j = 1,2; i ≠j), причем 0 Условие d < b означает, что если цены товаров обеих фирм вырастут на бесконечно малую величину ε, объем спроса на оба товара сократится. Условие а > АС(b-d) означает, что если обе фирмы назначат цены на уровне предельных издержек, объемы спроса на их товары будут положительными. Определим результат взаимодействия фирм, то есть найдем такой набор цен (P1*, P2*) что Рi* обеспечивает максимизацию прибыли π = (Рi - АС)Qd(Рi, Pj); i=1,2; j≠i. Вычислим для любого Pj функцию реакции i-й фирмы, максимизирующую (Рi - АС)Qd(Рi, Рj). Пусть Ri(Рj) - функция реакции фирмы на цену конкурента. Для рассматриваемого примера функция реакции будет иметь вид: Известно, что функции реакции обеих фирм симметричны. Решив систему из двух уравнений - функций реакций фирм, - получим следующий результат: При такой комбинации цен двух фирм они будут получать положительную прибыль, так как то есть разница между равновесной ценой и предельными (и средними) издержками положительна для каждой фирмы. Итак, дифференциация продукта смягчает ценовую конкуренцию. В большинстве случаев производители сами выбирают степень дифференциации продукта. Модель Эджворта Модель Эджворта является еще одной версией модели Бертрана, которая определяет ценовую конкуренцию фирмы с ограниченными размерами выпуска. Рассмотрим, установление равновесия на рынке при ценовом взаимодействии двух фирм ограниченности их совокупных мощностей. Предположим, что выпуск каждой фирмы, действующей в отрасли, ограничен величиной К, составляющей половину того объема выпуска отрасли, на который предъявляется спрос при цене, равной предельным издержкам. Это означает, что кривые средних и предельных издержек каждой фирмы имеют вертикальный вид при q = К: предельные издержки производства следующей единицы можно считать стремящимися к бесконечности. Если обе фирмы назначают цену Р = МС, их совокупный выпуск (Q = К1 + К2) достаточен, чтобы удовлетворить отраслевой спрос. Если фирма 1 увеличит свою цену, потребители захотят покупать товар фирмы 2, предлагающей более низкую цену. Однако половина потребителей не смогут купить продукт из-за ограниченности производственных возможностей фирмы 2. Они будут вынуждены покупать продукт у фирмы 1 по высокой цене. Фирма 1 столкнется с остаточным спросом RD1 (рис. 4.2), причем QRD1(Р) = QD(Р) – К2. По отношению к этому остаточному спросу фирма 1 будет действовать как монополист, максимизируя прибыль там, где МRrd1 – МС1. Цена фирмы 1 будет установлена на уровне Р1 > Р2 = МС, так что фирма 1 будет получать положительную экономическую прибыль, в то время как прибыль фирмы 2 останется равной нулю, несмотря на ее большую долю рынка. 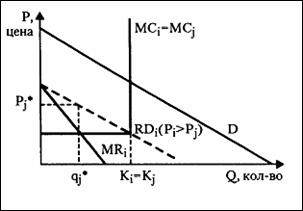 Рис. 4.2. Модель Эджворта В следующий период фирма 2 опустит свою цену до уровня ниже P1 - цены первого периода фирмы 1 так, чтобы переманить покупателей фирмы 1. Однако, поскольку производственные мощности фирмы 2 ограничены, она сможет удовлетворить только две трети рыночного спроса. В этот период фирма 2 продаст в два раза больше, чем фирма 1, почти по той же цене, в результате чего прибыли фирмы 1 удвоятся. Еще через период фирмы будут постепенно по очереди снижать цены до тех пор, пока одна из фирм не установит цену Рк на уровне, при котором за счет роста объема продаж (внутри, ограничений, налагаемых производственными мощностями) ее прибыль не окажется равной прибыли при наивысшей цене Рk = Р1: 0.5(P1 - MC)K = (Pk - MC)K С этой точки зрения другая фирма может попытаться поднять цену до уровня Р1. В результате начнется новый цикл последовательного снижения цен фирмами. Таким образом, статическое равновесие с одной ценой никогда не будет достигнуто; уровень цен будет последовательно подниматься и опускаться в интервале Рк < Р Рассмотрим пример. Предположим, рыночный спрос выражается формулой: Qd = 100 - Р, где Qd - величина спроса, в тыс. шт.; Р - рыночная цена. Пусть на рынке действуют две фирмы, предельные издержки которых постоянны, одинаковы и равны 10. Мощности каждой фирмы ограничены объемом в 45 тыс. шт. (К1 = К2 = 45). Равновесие Бертрана в данных условиях достижимо (q1 = q2 = 45; Р = 10), но оно не является равновесием по Нэшу. Докажем это. Пусть первая фирма назначает цену P1 = 10. Ее объем предложения будет равен q1 = K1 = 45. Тогда вторая фирма может максимизировать свою прибыль по остаточному (после первой фирмы) спросу: Максимизация прибыли обеспечивается ценой Р2 = 32.5 и объемом продаж q2 = 22,5. Вторая фирма получает прибыль π = 506,25 - это минимальная прибыль, которую может иметь вторая фирма, ориентируясь на остаточный спрос. Таким образом, стратегия «назначать цену на уровне предельных издержек» не является равновесием по Нэшу ни для одной фирмы, так как отклоняясь от этой стратегии фирма увеличивает свою прибыль. Совокупное предложение рынка в этих условиях составит: Qd = q2 + K1 = 67.5 Итак, если P1 достаточно низкая, второй фирме имеет смысл максимизировать прибыль по остаточному спросу. Ситуация меняется, если цена первой фирмы Р1 достаточно высока. Предположим, Р1 = 40. Тогда если вторая фирма назначит цену, меньшую цены первой фирмы (например, Р2 = 39), она получит весь спрос рынка: QRD2(P2 = 39) = 61 >K2. В этом случае объем остаточного спроса на товар второй фирмы превысит ее максимальный выпуск. Соответственно, объем ее продаж будет равен максимально возможному выпуску. Прибыль составит π2 = 1755 - что выше, чем если бы фирма ориентировалась на остаточный спрос. В общем виде прибыль второй фирмы (в том случае, если цена первой фирмы достаточно высока) составит: где ε - бесконечно малая величина; АС2 - средние издержки второй фирмы. У каждой фирмы есть две возможные стратегии:
Qrdi = Qd – Kj.
Pi = Pj – ε. Для рассматриваемого примера первая стратегия приносит фирме прибыль πi = 506,25; вторая- πi = (Pj - ε - ACi)Ki. Найдем минимальное значение P1, при котором второй фирме выгодно снижать цену. Пренебрегая бесконечно малой величиной, условие предпочтительности ценовой конкуренции составит: (Р1 - 10) 45 > 506,25. Откуда P1 > 21,25. Таким образом, ценовая конкуренция приносит большую прибыль только в том случае, если конкурент на рынке устанавливает достаточно высокую цену. Поскольку цена фирмы известна, а цена конкурента опустится достаточно низко, интервал возможных колебаний цен на рынке определится как Pi, Pj € [21,25; 32,5], где нижнее значение обеспечивается минимальным уровнем цены при выборе фирмой стратегией снижения цены, а верхнее значение представляет собой цену при выборе фирмой стратегии максимизации прибыли по остаточному спросу. Мощность играет на рынке роль фактора, ограничивающего возможности и стимулы ценовой конкуренции. Следовательно, выбор мощности играет роль предварительной договоренности фирм о масштабах ценовой конкуренции. Покажем это на примере, предположив, что мощности фирм существенно выше. Пусть K1 = K2 = 80. Тогда соответствующий интервал цен будет равен Р1, P2 € [10,71; 15]. Чем выше мощности фирм, тем уже интервал возможных цен и тем ближе цены, назначаемые фирмами на рынке, к средним издержкам. Пусть, К1 = К2 = 30. Тогда, максимизируя прибыль по остаточному спросу, фирма выберет объем продаж, равный 30 и назначит цену, равную 40, получив прибыль, равную 900. Далее, фирме выгодна ценовая конкуренция только при условии (P1 - 10)30 > 900, то есть если цена конкурента превышает 40.В данном случае получаем единственную цену рынка P1 = Р2= Р* = 40, ценовая война между фирмами исключена. Парадокс Бертрана разрешается благодаря:
Три названных характеристики служат важнейшими условиями, ограничивающими ценовую конкуренцию. И служат объектом стратегического выбора. Таким образом, доказана оправданность использования моделей (где стратегической переменной служит количество) в качестве инструмента анализа олигополии. Фирмы, желающие исключить ценовую войну между собой, выберут производственные мощности, равные равновесному объему выпуска в другой модели поведения олигополии - модели Курно. Модель Курно Цель модели заключается в том, чтобы показать каким образом устанавливается равновесный объем продаж на рынке, если фирма выбирает количество в зависимости от того, которое продает на рынке другая фирма. Фирмы выбирают объем продаж одновременно - обе они проводят «недальновидную» политику. Из-за этого, реакция контрагента приводит к тому, что ожидаемый фирмой выпуск контрагента может отличаться от фактического. Равновесие на рынке достигается тогда, когда ожидания каждой фирмы относительно объема выпуска конкурента реализуются. Пусть фирма 1 ожидает, что фирма 2 произведет q2 количества товара. Тогда фирма 1 решает произвести q1 единиц товара. Совокупный объем продаж отрасли составит Q = q1 + q2. Этот объем будет продан по цене Р(Q) = P(q1 + q2) Фирма 1 стремится к максимизации прибыли. Максимум прибыли достигается при таком объеме производства фирмы 1, когда ее предельные издержки равны ее предельной выручке: МС = МR, то есть: Такое же условие максимизации прибыли можно записать и для фирмы 2. Поскольку по условию каждая фирма выбирает объем своего производства, исходя из предположения о размере выпуска другой фирмы, оптимальный объем производства фирмы 1 будет зависеть от ожидаемого объема производства фирмы 2: q1 = f(q2exp) оптимальный объем производства фирмы 2 будет зависеть от ожидаемого объема выпуска фирмы 1: q1 = h(q2exp), где f и h - функции реакции первой и второй фирм соответственно, (qiexp - ожидаемый j-й фирмой выпуск i-й фирмы, i, j = 1,2; i ≠ j). Если ожидания фирм не оправдываются, q1 ≠ q1exp q2 ≠ q2exp фирмы пересматривают как предположения, так и свой собственный объем производства в соответствии с реальным выпуском другой фирмы. В результате меняется совокупное предложение отрасли и рыночная цена. Стабильное равновесие на рынке устанавливается тогда, когда ожидаемые выпуски фирм равны их реальным объемам производства, причем реальный выпуск и является оптимальным: Другими словами, каждая фирма выбирает такой оптимальный объем производства, какой ожидает от нее другая фирма. Такое равновесие называется равновесием Курно. Пусть функция рыночного спроса линейна и имеет вид где а - параметр спроса; q1, q2 - объемы выпуска фирм 1 и 2. Предельные издержки фирм одинаковы, постоянны и равны МС. Тогда условие максимизации прибыли для первой и второй фирмы соответственно будет иметь вид Отсюда функции реагирования для каждой фирмы составят: Эти уравнения описывают все комбинации q1 и q2, которые приносят максимальную прибыль каждой фирме. Поскольку фирмы идентичны, в равновесии они будут производить одинаковое количество товара, то есть Общий объем продаж в отрасли составит 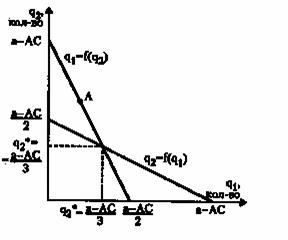 Рис. 4.3. Модель Курно Если кривые реакции изобразить графически (рис. 4.3.), равновесие Курно достигается в точке их пересечения. Именно здесь ожидаемые объемы двух фирм совпадают с их реальными величинами. Механизм достижения равновесия приходит следующим образом. В точке А фирма 1 произведет большее количество товара, чем от нее ожидает фирма 2. В результате фирма 2 будет вынуждена сократить свой объем выпуска в следующем периоде. В то же время фирма 1 в расчете на большое количество товара фирмы 2 тоже сократит свой выпуск. Когда и эти ожидания не оправдываются, фирмы будут корректировать объемы производства до тех пор, пока не будет достигнута точка равновесия, пока их ожидания не будут оправдываться. Рассмотрим равновесие Курно для n фирм. Предположим, что на рынке действует несколько фирм, каждая из которых проводит стратегию, соответствующую предпосылкам модели. Другими словами, каждая фирма на рынке выбирает оптимальный объем производства, исходя из своих ожиданий относительно объемов производства других фирм. Если число фирм на рынке равно n, то общий объем предложения составит величину Q = q1 + q2 +…+ qn. Каждая фирма, максимизируя прибыль, будет производить такой объем, чтобы: то есть Каждая фирма ожидает, что другие участники рынка сохраняет свой объем продаж неизменным. Поэтому с ее точки зрения изменение объема продаж на рынке совпадет с изменением ее собственных продаж, dQ = dqi. Домножим второе слагаемое в левой части на выражение PQ/PQ. Поскольку произведение где qi/Q- доля выпуска данной фирмы в общем объеме производства отрасли, qi/Q = Y. Тогда цена на рынке и индекс Лернера монопольной власти Эта формула показывает зависимость рыночной цены и монопольной власти фирм, действующих на рынке, от числа фирм и их рыночной доли. Если Yi стремится к нулю (ситуация свободной конкуренции), цена стремится к уровню предельных издержек: Р(Q) = МС. Если Yi = 1 (рынок монополии). Получаем формулу монопольной цены: Р(Q) = МС/[1+1/Еd]. Соответственно, промежуточные случаи расположены между этими крайними ситуациями. Таким образом, равновесие Курно позволяет связать воедино разные рыночные структуры. Модель Штакельберга В предыдущих моделях предполагалось, что фирмы обладают одинаковой рыночной силой, и их поведение определяется одновременно. Рассмотрим ситуацию, когда фирмы неодинаковы по силе, а выбор объема производства осуществляется последовательно: сначала объем производства определяется для более «сильной» фирмы, затем «слабая» фирма выбирает свою линию поведения. При этом исходим из того, что фирмы, выбирая мощность, устанавливают границы ценовой конкуренции и барьеры входа для потенциального конкурента. Модели Эджворта и Курно показывают, каким образом выбор производственной мощности влияет на ценовую конкуренцию и какие мощности выбирают фирмы, принимая решения одновременно, с тем чтобы исключить ценовую войну. Рассмотрим, какую производственную мощность должен выбрать лидер, учитывая будущую реакцию другой фирмы (или фирм) на свои действия. Пусть фирмы выбирают, какое количество товара производить, а цена устанавливается рынком. Предположим, фирма 1 является лидером на рынке и принимает решение относительно величины выпуска независимо, в то время как фирма 2 корректирует свое поведение, исходя из того выбора, который сделала фирма 1. Тогда цель фирмы 2 заключается в том, чтобы максимизировать прибыль при заданном объеме производства фирмы 1: Реакция фирмы 2 состоит в максимизации прибыли q2 = h(q1) В случае линейной функции спроса Р = a - q1 – q2 функция реакции фирмы 2, как было показано выше, Рассмотрим поведение фирмы-лидера (фирма 1). Фирма-лидер, знает, что ее выбор объема производства оказывает влияние на размер выпуска фирмы 2, а следовательно, на общий объем предложения отрасли, рыночную цену и в конечном итоге прибыль самой фирмы-лидера. Поэтому для нее условие максимизации прибыли принимает вид: То есть В примере условие максимизации прибыли лидера будет выглядеть: Откуда Общий объем предложения отрасли равен: Прибыль лидера в модели Штакельберга вдвое превышает прибыль последователя. 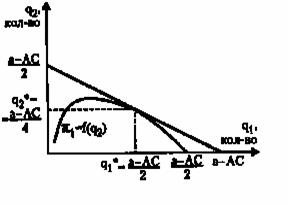 Рис. 4.4. Модель Штакельберга Стратегическое поведение лидера, учитывающее будущую реакцию конкурента на рынке, приносит ему «преимущество первого хода». Применение той или иной модели зависит от характеристик рынка и возможностей фирмы влиять на рыночную цену или объем выпуска. Модели Курно и Штакельберга применяются при исследованиях рынков, когда у фирм существуют фиксированные производственные планы, так что относительно трудно изменить количество выпускаемого продукта, если план уже принят. Это характерно для отраслей с длительным сроком изготовления товара (тяжелая промышленность, самолетостроение, производство уникального оборудования, судостроение и т. д.), а также для тех отраслей, где фирмам необходимо инвестировать значительные средства в специализированное оборудование для сбыта данного товара (например, строительство крупного универмага). На таких рынках изменение цен товаров более вероятно, чем изменение объемов продаж. Модели Бертрана и Эджворта применяются в тех случаях, когда фирмам сложнее корректировать принятые цены. Примерами могут служить продажи по каталогам, тендеры, аукционы, причем преимущественно в отраслях, производящих товары потребительского назначения. В этом случае, напротив, изменение цен менее вероятно, чем изменение объемов продаж. Кооперативные модели поведения олигополистов Некооперативные модели взаимодействия фирм на олигопольном рынке не всегда ведут к стабилизации параметров рынка и к установлению единственной равновесной цены, что затрудняет крупным фирмам получение положительной прибыли в долгосрочном периоде. И хотя рынок выработал ряд способов смягчения подобных ситуаций, некооперативное взаимоотношение фирм по-прежнему остается далеким от совершенства типом поведения на рынке. На олигопольном рынке у фирм есть стимулы координировать свою производственную деятельность и политику ценообразования посредством ограничения объема выпуска фирм (квот) и назначения одинаковых цен для увеличения совокупной прибыли отрасли и индивидуальных прибылей каждой из фирм. Ассоциация фирм, которые заключили явное или тайное соглашение о координации своей деятельности, называется картелем. Если картель включает все фирмы, действующие в отрасли, она становится монополией, и фирмы получают монопольную прибыль. Фирмам выгодно заключать картельные соглашения. Но если картель уже сформирован и эффективно ограничивает выпуск и цену на рынке, у каждой фирмы появляется стимул нарушить картельное соглашение путем увеличения квот выпуска или понижения цены. Для поддержания картельных соглашений в течение продолжительного времени требуются дополнительные усилия продавцов-участников соглашения. Известно, что фирмы, действующие в условиях свободно конкурентного рынка, максимизируют прибыль. Каждая фирма рассматривает уменьшение своего выпуска только с точки зрения своих собственных выгод и не учитывает последствия своих действий для конкурентов (других фирм), хотя сокращение выпуска даже одной фирмы в отрасли выгодно и всем прочим, поскольку уменьшает совокупное предложение отрасли и увеличивает равновесные цены. Таким образом, возникает своего рода внешний эффект, который в условиях свободной конкуренции не принимается во внимание. Картельное соглашение учитывает эти последствия действий одной фирмы для увеличения прибыли всех участников. Поэтому картель как отрасль производит меньше объема, чем рынок свободной конкуренции. Картель интернализирует внешние эффекты сокращения выпуска каждой фирмы для остальных фирм, так что последствия этих внешних эффектов становятся внутренним делом картеля (например, в форме распределения дополнительных прибылей или определения квот выпуска). Рассмотрим модель картеля для отрасли и для каждой фирмы. Пусть картель охватывает все фирмы отрасли. Тогда поскольку картель представляет собой монополию, равновесие в отрасли достигается там, где предельные издержки отраслевого выпуска соответствуют предельной выручке от его продажи (рис. 4.6). Соответственно, цена на рынке установится на уровне Рm. Если цена равна Рm, каждая фирма заинтересована в повышении выпуска до тех пор, пока ее предельные издержки не окажутся равными этой цене, то есть до уровня qi. Сравним с условиями свободной конкуренции: цена - Рс, объем выпуска фирмы - qc. Поскольку конкурентная цена ниже картельной, а функция предельных издержек фирмы возрастает, картельный объем выпуска фирмы всегда будет меньше конкурентного. Однако каждая фирма в рамках картеля имеет стимул наращивать выпуск до пределов, превышающих то количество, которое она выпускала бы на рынке совершенной конкуренции. Рис. 4.6. Сравнение картеля и рынка совершенной конкуренции В рамках статичной модели картеля каждая фирма-участник оказывается заинтересованной в нарушении картельного соглашения. Вывод может измениться, если проанализируем влияние решений фирмы не только на сегодняшнюю прибыль, но на весь поток ожидаемой будущей прибыли. Очевидно, что в долговременной перспективе фирма может быть заинтересована придерживаться установленной для нее квоты. Рассмотрим условия, при которых картельное соглашение является стабильным и соответственно нестабильным. Пусть π Фирма будет нарушать картельное соглашение в том случае, когда: Предположим, что фирмы-участники картеля действует по стратегии копирования . Если фирма нарушает соглашение, например, назначая более низкую, чем картельная, цену, она в первый период (период нарушения соглашения) получает прибыль Рс, но в следующий период ее ловят и наказывают (в виде ограничения продаж, дискриминации со стороны других участников картеля или штрафа, либо в виде сокращения прибыли из-за разрушения картельного соглашения) величиной Н ежегодных вычетов до конца ее существования (то есть для бесконечного периода времени) где δ - дисконтирующий множитель; ρ - вероятность повторных продаж фирмы-нарушителя в следующем периоде. Общая сумма ожидаемой прибыли фирмы-нарушителя соглашения составит: Если фирма придерживается соглашения, текущая ценность ее ожидаемой прибыли составит Фирме выгодно не нарушать картельного соглашения, если нарушение не приносит ей роста текущей ценности ожидаемой прибыли: или (4.31) Итак сохранение картельного соглашения тем выгоднее фирме:
Для сохранения картеля его участники должны повысить сумму штрафа, налагаемую на нарушителя, и сделать угрозу штрафа более правдоподобной. К факторам, облегчающим сохранение картельного соглашения и поддержания дисциплины в картеле, относятся следующие:
Выполнение этого условия существенно зависит от эластичности рыночного спроса и от доли фирм в отрасли, которые входят в картель. Чем менее эластичен спрос в отрасли, тем легче предпринимать действия по увеличению цены, тем выше может быть уровень картельной цены и совокупной выручки фирм. С другой стороны, если картель контролирует только незначительную долю отраслевого рынка, фирмы-аутсайдеры могут воспрепятствовать значительному увеличению рыночной цены. Даже когда все фирмы отрасли входят в картель, высокая норма отраслевой прибыли может привлечь новых конкурентов, и если барьеры для ; входа на рынок незначительны, картель не сможет удержать высокие цены (и прибыли) в долгосрочном периоде.
Если фирмы-участницы картеля ожидают, что картельное соглашение будет вскоре обнаружено правительством, за чем последуют строгие санкции, фирмы будут менее склонны к заключению такого рода соглашений, и наоборот: чем ниже риск обнаружения картельного соглашения антимонопольными органами и использования строгих санкций, тем выше стимулы объединения и поддержания картеля.
Издержки по организации картеля включают в себя, прежде всего, затраты по ведению переговоров между предполагаемыми участниками. Факторами, от которых зависит величина этих издержек являются:
Длительная история существования картелей выработала специфические методы предотвращения нарушения картельных соглашений, каждый из которых нацелен на повышение угрозы наказания в случае оппортунистического поведения, с одной стороны, и на обеспечение возможно более длительного существования картеля - с другой. К основным методам предотвращения нарушения картельного соглашения относятся:
Эффективные картельные соглашения включают спецификацию не только продажной цены, но и других показателей, которые легче проконтролировать, таких как: квота производства, ограничения покупки/продажи в отношении дилеров, нормы расходов на НИОКР, территориальные и/или продуктовые ограничения маркетинговой и сбытовой деятельности;
Каждому участнику выделяется особая территория или особый класс потребителей, так что контроль за соблюдением соглашения значительно облегчается, а последствия нарушения уменьшаются (поскольку оказывают влияние только на выделенную область деятельности);
Картельное соглашение может включать в себя условие о том, что продавец не будет продавать другим покупателям/дилерам по цене ниже установленного картелем уровня для данного класса товаров или потребителей;
Члены картеля могут договориться о том, что если цена на рынке падает ниже определенного заранее уровня (контрольной цены), каждая фирма-участник получает право осуществлять политику самостоятельно, в том числе расширять выпуск. Картель при этом фактически распадается, а период получения дополнительной прибыли фирмой-нарушителем сокращается. | ||||||||||||||||||||||||||
