Теория Жана Пиаже. Теория Пиаже (Жан Пиаже)

• Название: Теория Пиаже (Жан Пиаже)
• Анкор: Теория Жана Пиаже.docx
• Дата: 22.09.2018
• Размер: 133.26 Kb.
• Имя файла: Теория Жана Пиаже.docx
• Тип: Документы; #24953
• страница: 4 из 5

VII. Уравновешивание и когнитивные структуры

23. Главная цель теории развития - объяснить построение операциональных структур интегрированного целого или тотальности (structure operatoire densembie), и, как мы считаем, только гипотеза прогрессирующего уравновешивания может сделать это. Чтобы понять это, нам прежде необходимо вкратце рассмотреть сами операциональные структуры.

Понятие структуры стало классическим в психологии с тех пор, как было использовано гештальттеорией, чтобы разбить ассоциализм и его атомистические привычки мышления. Но гештальтисты считали, что достаточно всего одного типа структуры, применимого как к восприятию, так и к интеллекту. Они не различали две особенности, на самом деле совершенно отличные друг от друга. Первая является общей для всех структур - все они обладают целостными законами, выведенными из их системной формы, и эти законы отличны от свойств элементов, входящих в целостность. Вторая особенность - это неаддитивная композиция, т. е. то, что целое количественно отличается от суммы своих частей (как в перцептивной иллюзии Оппеля). Но в сфере интеллекта существуют структуры, подтверждающие первую особенность, но отнюдь не вторую; множество целых чисел, например, обладает целостными свойствами как таковыми ("группа", "кольцо" и т. п.), но композиция в нем строго аддитивна: 2+2=4 - ни больше, ни меньше.

Поэтому мы попытались определить и проанализировать структуры, специфичные интеллекту, а это структуры, включающие операции, т. е. интериоризованные и обратимые действия, такие, как сложение, логическое умножение, или, другими словами, композиция множества классов или отношений, рассмотренных "разом". Эти структуры в мышлении ребенка развиваются очень естественно и спонтанно. Например, сериация (т. е. упорядочивание предметов сообразно их размеру), класеификация, установление взаимно-однозначных или многозначных соответствий, построение мультипликативной матрицы - все эти структуры появляются в возрасте между 7 и 11 годами на уровне, называемом нами уровнем "конкретных операций", имеющих дело непосредственно с объектами. После 11-12 лет появляются другие структуры, такие, как "группа четырех" и комбинаторика (мы обсудим их ниже).

Для того чтобы изучить свойства этих конкретно-операциональных структур и установить их законы, необходимо использовать язык логики классов и отношений, но это не будет означать, что мы оставим область психологии. Когда психолог вычисляет вариативность выборки или использует факторный анализ, это не означает, что его областью становится статистика, а не психология. Чтобы анализировать структуры, нам необходимо сделать то же самое, но поскольку мы имеем дело не с количествами, необходимо прибегнуть к более общим математическим инструментам, таким, как абстрактная алгебра или логика. Но они будут являться только инструментами, которые позволят достичь подлинно психологических сущностей, таких, как операций, понимаемые как интериоризованные действия или общие координации действий.

Целостная структура, такая, как классификация, обладает следующими свойствами, характеризующими операции, которые действительно присутствуют в действиях субъекта.

a. Субъект может комбинировать один класс A с другим A¹, чтобы получить класс В, обозначаемый А+А¹=В (затем он может продолжить, составив В+В¹=С и т. д.).

b. Он может диссоциировать А или А¹ от В. Это обозначается как В-А¹=A (что составляет обратную операцию). Заметим, что эта обратимость необходима для понимания отношения А<В, а мы знаем, до 7 или 8 лет ребенок с трудом понимает, что если дано 10 желтых цветов A и 10 других цветов А¹, то цветов В больше, чем желтых цветов А, потому что для сравнения целого В с его частью А необходимо объединить две операции А+А¹=В и А=В-А¹ в ином случае целое В не будет сохраняться, и А затем будет сравниваться только с A¹.

c. Он будет понимать, что А-А=0 и А+0=А.

d. Наконец, он будет способен к ассоциативности (А+А¹)+B¹=А+(А¹+B¹)=С, но при этом (А+А)-А не эквивалентно А+(А-А)=А.

Эти элементарные структуры группирования (structures de groupoides) мы назвали группировками (Группировка может рассматриваться как решетка, которая может быть обратимой. В решетке, если А+А¹=В, где В - наименьший верхний предел А и А¹, А может быть вновь получен посредством операции с В: В-А¹=А. Но более общим случаем является, когда С есть, например, наибольший нижний предел А и C¹ и А≠D-С¹. Другими словами, операция А+А¹ может быть "обращена" только на смежных элементах, таких, как Л и Л1, в том смысле, что в триплете А, А¹, В любые два элемента единственным образом определяют третий элемент. Это несправедливо в случае А, С¹, D, где А+С¹=D-D¹-В¹-А. Здесь мы рассмотрим группировку как группу, где композиция ограничена только смежными элементами (композиция А+С, например, не может быть определена без специальных условий) и специальными тождественностями А+А=А, А+В = В. Группировка поэтому определяется только как последовательность включений элементов, такая, как классификация. Она состоит из (а) прямой операции, (b) обратной операции, (с) тождественной операции и (d) специальных тождеств:

А+А¹=В

В-А¹=А

А+O=А; А-А=O

А+А=А; -А-А=-А

А+В=В). Группировки не только гораздо более примитивны, чем математические группы, но и гораздо более ограничены и менее элегантны, поскольку композиция в них определяется только смежными элементами и полной ассоциативностью (Ассоциативность ограничена тем фактом, что в группировке композиция определена только на смежных элементах; А+С¹ может быть построена только посредством последовательных операций композиции включенных смежных классов А, А¹, В вплоть до D - первого класса, содержащего как А, так и С¹, тогда А+С¹=D-В¹-А¹. Сходным образом А-С¹ дает начало только тавтологии А-C^l=(D-О-В¹-А¹)-С¹, где D-С¹-B¹-А¹=А; следствием этих ограничений является то, что ассоциативность не может быть проверена до тех пор, пока не будет проведена "редукция" заключенных в скобки элементов: (А+А)+В¹=В+В¹=С, но А+(А¹+В¹) не имеет никакого значения, поскольку композиция (А¹+В¹) как таковая не определена относительно других правил редукции (Piaget, 1959). Напротив, в группе целых чисел по сложению всякое число может немедленно прибавляться к любому другому (или вычитаться из него), поскольку целое число может быть полностью освобождено от следующих за ним чисел, которые его "содержат"). Нас часто критиковали за то, что построенные таким образом структуры не имеют психологической реальности. Но эти структуры действительно существуют прежде всего потому, что описывают просто то, что происходит при классификации сериации и т. п. - формах поведения, появляющихся совершенно одновременно. Более того, на психологическом уровне их можно опознать с помощью более общих характеристик, открывающих существование целостной структуры, таких, как транзитивность (например, в сериации А<С, если А<В и В>С) и установление понятий сохранения (сохранения целого В, когда порядок его частей А и А¹ изменяется, сохранение длины, количества и т. п.).

24. Выясним, как могут появляться и развиваться фундаментальные структуры интеллекта и те структуры, которые выводятся из них позднее. Поскольку они не врождены, их нельзя объяснить одним созреванием. Логические структуры не являются простым продуктом физического опыта; в случае сериации, классификации, установления взаимно-однозначных соответствий деятельность субъекта добавляет к объектам новые отношения, такие, как порядок или целостность. Логико-математический опыт выводит свою информацию из действий самого субъекта (как мы видели в п. 21), что предполагает авторегуляцию данных действий. Можно было бы предполагать, что эти структуры якобы являются результатом социальной или педагогической передачи. Но, как мы видели (п. 22), ребенок должен ранее понимать то, что передается, а для этого необходимы структуры. Объяснение на основе социального воздействия только замещает одну проблему другой: как сами члены социальной группы первично приобрели данные структуры?

Но на всех уровнях развития действия координируются путями, уже включающими некоторые свойства порядка, включения и соответствия, которые предвещают соответствующие структуры (например, структуры сериации для отношений порядка, классификации для включения, мультипликации для соответствий). И, что еще важнее, координация действий включает корректировку и саморегуляцию; действительно, мы знаем, что регуляторные механизмы характерны для всех уровней органической жизни (это справедливо как для генофонда, так и для поведения). Но регуляция является ретроактивным процессом (негативной обратной связью), предполагающим начало обратимости, так что становится явным отношение, существующее между регуляцией (полуобратимой коррекцией ошибок путем ретроактивного действия) и операцией, полная обратимость которой допускает исправление будущей ошибки наперед (например, "совершенную" регуляцию в кибернетическом смысле).

Поэтому в высшей степени правдоподобно, что построение структуры является во многом делом уравновешивания, определенного не как равновесие между противоположными силами, но как саморегуляция, т. е. уравновешивание есть ряд активных реакций субъекта на внешние возмущения, которые могут обладать разной степенью эффективности. Таким образом, уравновешивание становится тождественным обратимости; но, когда некоторые возражают (Брунер, например), что уравновешивание становится излишним и ненужным, поскольку достаточно одной обратимости самой по себе, они забывают, что таким образом может быть рассмотрено только финальное состояние равновесия, а необходимо объяснить главным образом уравновешивание как процесс саморегуляции, ведущий к данному финальному состоянию и поэтому к обратимости, характеризующей структуры.

25. Уравновешивание имеет объяснительную ценность вследствие того, что основывается на процессе с последовательно возрастающими вероятностями. Лучше понять это можно на конкретном примере. Как можно объяснить тот факт, что, когда на глазах ребенка круглый пластилиновый шарик раскатывается в "колбаску", ребенок начинает с отрицания сохранения количества пластилина при такой трансформации, а кончает (с возрастом) утверждением логической необходимости его сохранения? Чтобы найти объяснение, необходимо определить четыре стадии, каждая из которых возрастает в вероятности, не a priori, но как функция наличной ситуации или ситуации, немедленно предшествовавшей ей.

a. Первоначально ребенок рассматривает только одно измерение, например длину (скажем, в 8 случаях из 10). Тогда он говорит, что колбаска содержит больше пластилина, потому что она длиннее. Иногда (скажем, в 2 случаях из 10) он говорит, что колбаска уже, упуская из виду, что она длиннее, и из этого заключает, что количество вещества уменьшилось. Почему он рассуждает таким образом? Просто потому, что вероятность обратить внимание только на одно измерение больше. Если вероятность для длины 0,8, а для толщины 0,2, то вероятность для длины и толщины вместе только 0,16 потому, что до тех пор, пока нет понятия о компенсации, изменения в длине и ширине выступают для ребенка как независимые события.

b. Если колбаску все более и более вытягивать или если ребенок устает от повторения одной и той же аргументации, вероятность обратить внимание на другое измерение становится больше, чем в начале, и ребенок будет колебаться в своей оценке между двумя измерениями.

с. Если существуют колебания, то для субъекта вероятность заметить определенную корреляцию между двумя изменениями (то, что, когда колбаска вытягивается, она утоньшается) становится больше (третья стадия). Но как только появляется чувство солидарности, существующей между изменениями, мышление ребенка приобретает новое качество: оно уже более не полагается целиком на конфигурации, но начинает интересоваться трансформациями: колбаска не просто "длиннее", она может "удлиняться" и т. д.

Как только мышление субъекта принимает в рассмотрение трансформации, становится более вероятной oновая стадия, на которой он понимает (по отдельности или одновременно), что трансформация может быть oобращена или что две симультанные трансформации длины и толщины компенсируют друг друга вследствие солидарности между ними, которую он мельком заметил (см. стадию {с)).

Отсюда видно, что прогрессирующее уравновешивание имеет эффективную объяснительную ценность. Стадия (а), которую отмечали все проверявшие наше исследование, не является точкой равновесия, поскольку ребенок замечает только одно измерение: в этом случае алгебраическая сумма возможных действующих компонентов (цитируя принцип физических систем Деламбера) не является равной нулю, поскольку один из них, состоящий в обращении внимания на другое изменение, еще не включен в нее, но рано или поздно может появиться. Поэтому переход с одной стадии на другую является уравновешиванием в самом классическом смысле слова. Но, поскольку такие замещения систем являются деятельностями субъекта и поскольку каждая из этих деятельностей состоит в коррекции немедленно предшествовавшей ей, уравновешивание становится последовательностью саморегуляций, ретроактивные действия которых в итоге приводят к операциональной обратимости. Последняя идет далее простой вероятности и достигает логической необходимости.

Все сказанное нами о данном случае операционального сохранения может быть повторено в отношении построения любой операциональной структуры. Например, сериация A<В<С становится операциональной в результате координации отношений (и) (каждый новый элемент Е упорядоченной последовательности обладает как свойством быть больше D, С, В, А, так и быть меньше F, G, Н, ...), и эта координация вновь является результатом процесса уравновешивания с последовательно возрастающими вероятностями того типа, который мы уже описали. Сходным образом для включения классов понимание, что А<В, если В=А+А¹ и А¹>0, достигается как результат уравновешивания этого же "типа.

Поэтому не было бы преувеличением сказать, что уравновешивание является фундаментальным фактором развития и что оно даже необходимо для координации трех остальных факторов.

VIII. Логико-математические аспекты структур

26. Все только что упомянутые "конкретные" операциональные структуры предполагают построение определенных количеств: величины классов для классификации (что объясняет трудность квантификации включений классов), размера различий для сериации, количественных сохранений и т. п. Но даже до построения этих количественных структур на дооперациональных уровнях могут наблюдаться определенные частичные качественные структуры, которые имеют большой интерес, потому что составляют, так сказать, первую половину логики обратимых операций. Это ориентированные функции (однонаправленные функции, не имеющие инверсий, которые предполагали бы обратимость) и качественные тождественности (см. п. 10).

Функции, как мы помним, являются "чертежами" в математическом смысле, которые не имеют инверсий, потому что, как мы видели, психологически связаны с целенаправленными схемами действий. Предположим, например, что экспериментатор держит в руках один конец веревки (в), перекинутой через блок, а к другому ее концу подвешен груз, так что одна часть веревки (а) находится под прямым углом к другой ее части (а¹). Все дети в возрасте от 4 до 7 лет понимают, что если потянуть за веревку, то одна ее часть (а) станет короче, а другая часть (а¹) длиннее. Но они все еще не обладают понятием сохранения длины всей веревки (в) (в=а¹+а), и то, что они осуществляют, это не квантифицированная операция, а просто инверсное или ординальное приравнивание (длиннее = дальше).

Сходным образом в случае тождества, как мы видели, все дети (или почти все) соглашаются, что, когда пластилиновый шарик раскатывается в колбаску, он все равно остается "одним и тем же" куском пластилина, даже если количество его и не сохраняется. Подобные представления о тождественности приобретаются очень рано, и упомянутая нами в п. 2 схема постоянного объекта - одна из них. Брунер в своей книге рассматривает их как источник сохранения количеств. В известном смысле это верно (они составляют необходимое, но недостаточное условие), но при этом остается центральное различие: качества (на которых основывается качественная тождественность) могут быть установлены перцептивно, тогда как количества включают длительно вырабатываемую структуру, сложность которой мы только что видели (пп. 23-26). В действительности функции и качественная тождественность составляют только дооперациональную и качественную половину логики, они ведут к логике обратимых и количественных соответствий, но недостаточно могущественны, чтобы отвечать за нее.

27. Этот количественный аспект конкретных операций в противоположность качественной природе дооперациональных функций и тождественностей открывается, в частности, в построении (в возрасте 7-8 лет) операций, связанных с числом и измерением, частично изоморфных друг другу, но имеющих совершенно различное содержание. Построение количественных чисел не может объясняться просто установлением взаимнооднозначных соответствий между эквивалентными классами, как считали Рассел и Уайтхед, потому что использованные ими соответствия, отвлеченные от качеств (в противоположность качественным соответствиям между индивидуальными объектами, обладающими одними и теми же свойствами), имплицитно вводят единицу и число, что приводит к порочному кругу. В действительности, когда мы имеем дело с ограниченными совокупностями, количественные числа не могут быть диссоциированы от порядковых, подчиняясь трем следующим условиям.

a. Абстракция от качеств, делающая все отдельные объекты эквивалентными, и поэтому 1=1=1.

b. Упорядочение: 1->1->1..., которое необходимо для различения объектов друг от друга, иначе было бы справедливо равенство 1+1=1.

c. Включение (1) в (1+1), затем (1+1) и (1+1+1) и т. п.

Поэтому целые числа являются результатом синтеза упорядочивания (сериация) и включения (классификация), которые необходимы для абстрагирования от качеств. Отсюда целые числа строятся из чисто логических элементов (сериации и классификации), но последние реорганизуются, составляя новый синтез, допускающий квантификацию посредством процесса итерации: 1+1=2 и т. п.

Сходным образом измерение континуума (например, линии, поверхности) предполагает: (а) его разбиение на сегменты, один из которых затем выбирается в качестве единицы и приравнивается к остальным посредством конгруэнтности: а=а=а..., (b) определенное упорядочение этих единиц: а а... и т. п. и (с) приведение единиц в виде аддитивных композиций: а в (а+а) и (а+а) b(а+а+а). Таким образом, данный синтез разбиения и включения сегментов и упорядочения изоморфен синтезу упорядочения и включения, характеризующему число, что дает .возможность использовать число для измерения.

Поэтому ясно, что, не прибегая ни к чему другому, кроме синтеза элементарных "группировок" включения и порядка, субъект достигнет числовой или метрической квантификации, мощь которой далеко превосходит элементарные квантификации (отношения между частью и целым) классификаций или сериации, основанных на различениях, оцениваемых просто как "больше" или "меньше".

28. За конкретно-операциональными структурами, упомянутыми в п. 23, в возрасте 11-15 лет происходит построение двух новых структур, делающих возможной манипуляцию такими пропозициональными операциями, как импликация (p⊃q), несовместимость (p/q) и дизъюнкция (p∨q) и т. п. Такими новыми структурами являются "группа четырех" и комбинаторные операции. Комбинаторика на этой стадии состоит в классификации всех возможных классификаций (так же как перестановки являются сериацией сериации) аа, ab, ас, be, bb, се и т. п. и поэтому составляют не полностью новую операцию, но операцию над другими операциями. Сходным образом группа четырех INRC (Группа INRC - это группа операций, которые выполняются на операциях или элементах какой-либо другой алгебраической структуры и имеют инволютивную операцию (операцию, являющуюся своей собственной инверсией: N²=l). Примером инволютивной операции является закон двойственности (де Моргана) в булевой алгебре: p∨q=p∧q которыймыможемзаписать: N(p∨q)=(p∧q) (N обозначаетотрицание). ЕслимыопределимС (коррелятивность) какправило, котороедействуетнаотношениях, изменяя∧на∨инаоборот, и R (симметрию) какправило, котороедействуетпоотношениюкзнакамистинности, меняярнариобратно, то, используя последовательно С и R (скажем, на (p∨q)), мыполучимтотжерезультат, чтоиприиспользовании N. Следующаядиаграммаиллюстрируетотношениямежду N, R иС, применяемымив (p∨q):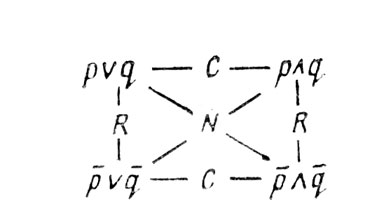



Тождественность I может быть определена как правило, которое изменяет любую формулу в самое себя, и посредством "прогона" по диаграмме легко может быть проверена последовательность следующих свойств: a. RC=N, RN-C, CN=R, и все пары обладают, коммутативностью RC=CR, etc. b. C²=N²-R²-I (все трансформации являются инволютивными, т. е. для каждого элемента определена инверсия). c. RNC=I. На основании этого можно показать, что группа INRC вместе с операцией композиции (понимаемой в обычном смысле слова как применение трансформации к результату другой) является группой четырех элементов, не составляющей кольцо (известной как "группа четырех" Клейна). Группа INRC также может быть определена на физической системе, имеющей соответствующую структуру (т. е. инволютивную трансформацию, которая может быть "разложена" на две другие инволютивные трансформации). Один из экспериментов Пиаже на системе с двойным отсчетом включал ситуацию: на маленькой дощечке находилась улитка, которая могла ползти слева направо и обратно, причем саму дощечку также можно было перемещать в обе стороны вдоль стола. Можно определить С как правило, обращающее перемещение улитки: C(Z, Z)=(R, Z), где (R, Z) означает, что улитка движется вправо, а дощечка - влево (первая координата). Тогда мы можем определить R как правило, обращающее перемещение вдоль второй координаты, например R(Z, Z)=(Z, R) (обращение перемещения дощечки). Диаграмма имеет ту же структуру, что и предыдущая, и N (N обращает перемещения по обеим координатам) будет являться результатом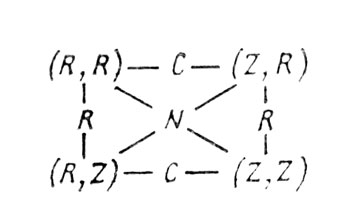



) является результатом объединения в целое инверсий N и реципрокностей R (поэтому появляется инверсия реципрокности С (NR=C), так же как и тождественная операция 1=NRC. Но инверсия уже существовала в группировках классов в форме А-А=0, а реципрокность - в группировках отношений в виде А=В, откуда В=А. Группа INRC, таким образом, вновь является операциональной структурой, имеющей отношение к предшествовавшим операциям. Что до пропозициональных операций p⊃q и т. п., которые включают как комбинаторику, так и группу INRC, то они новы по форме, но по своему содержанию относятся к связям между классами, отношениями или числами, и поэтому опыты являются операциями над операциями.

Вообще операции, принадлежащие третьему периоду развития (см. п. 10, период С для возраста 11-12 лет), уходят корнями в конкретные операции (подпериод (b.) между 7 и 11 годами), обогащая их, точно так же, как источник конкретных операций лежит в сенсомоторных схемах (период а, до 2 лет), которые они также значительно изменяют и обогащают. Поэтому последовательный характер стадий (который мы уже с достаточной силой подчеркнули в п. 10) с точки зрения построения структур соответствует механизму, который необходимо проанализировать, потому что он слишком важен для того, чтобы просто назвать его секвенциальным, или прогрессирующим, уравновешиванием. Сейчас необходимо понять, как происходят построения, приводящие к возникновению чего-то нового (что является хорошо известной проблемой развития математических структур).

29. Мы видели (п. 21, с), что уже до уровня построения логико-математических операций и поэтому до возникновения дедуктивных систем можно было говорить о логико-математических экспериментах, извлекающих информацию из свойств действия, выполненных на объектах, а не из самих объектов, что совершенно различные вещи. Поэтому в противоположность собственно абстракции в данном случае мы имеем новый тип абстракции, которую можно назвать рефлексивной и которая является ключом к интересующей нас проблеме. Чтобы абстрагировать свойство из действия или операции, недостаточно просто отделить его от тех свойств, которые в дальнейшем не будут приниматься во внимание (например, выделить "гформу" и отбросить "содержание"); свойство или форма, выделенные таким образом, должны быть дополнительно транспонированы куда-либо, т. е. перенесены в другой план действия или операции. В случае простой абстракции такой проблемы не возникает, поскольку тогда мы имеем дело со свойством объекта, ассимилируемым субъектом. Однако в случае рефлексивной абстракции, когда субъект извлекает свойство или форму из действий (операций) плана P₁, он должен затем перенести их в более высокий план Р₂, что является их отражением (рефлексом) в квазифизическом смысле (как при отражении луча света). Но для того чтобы данная форма или свойство были ассимилированы в новом плане Р₂, они должны быть реконструированы в этом новом плане и подвергнуты новому мыслительному процессу, который будет теперь означать "отражение" (рефлексию )в когнитивном смысле. Поэтому "рефлективную абстракцию" необходимо понимать в обоих смыслах.

Но если для ассимиляции свойств или форм, абстрагированных в плане P₁, необходим новый когнитивный процесс в плане Р2, то это означает, что новые операции или действия плана Р₂ будут добавлены к операциям или действиям плана Рь из которого была абстрагирована данная информация. Следовательно, рефлексивная абстракция по необходимости является конструктивной и обогащающей новыми элементами структуры, выведенные из плана Рь что равноценно построению новых структур. Это объясняет, почему конкретные операции, основанные на сенсомоторных схемах, богаче последних и почему то же самое справедливо для пропозициональных, или формальных операций, которые сами основываются на конкретных операциях. Как операции над операциями, они добавляют новые способы композиции (комбинаторику и т. п.).

Но рефлексивная абстракция является общим процессом построения в математике: например, она служила для выделения алгебры как группы операций над операциями арифметики. Таким же образом Кантор посторил трансфинитную арифметику: он поставил во взаимооднозначное соответствие последовательности 1, 2, 3, 4... и 2, 4, 6, 8. Это произвело новое число (N), выражающее "мощность (число) исчисляемого", но не принадлежащее никакой из последовательностей. Современная теория функций таким же образом строит "морфизмы" и т. п., и то же самое справедливо в отношении "материнских структур" Бурбаки.

Замечательно то, что процесс построения структур, который мы наблюдали в последовательных стадиях развития ребенка и в механизмах уравновешивания посредством саморегуляции (что имеет результатом саморегуляцию с помощью обратной связи высшего порядка, т. е. обратимой операции), совпадает с постоянным конструирующим процессом, используемым математикой в ее бесконечном продуктивном развитии. В этом состоит решение проблемы развития, несводимого ни к эмпирическому процессу открытия "уже готового" внешнего мира, ни к преформизму "ли предетерминизму (a priori), также означающим, что все "уже готово" от начала. Мы считаем, что истина лежит между двумя этими крайностями, т. е. в конструктивизме, выражающем тот способ, которым постоянно вырабатываются "овые структуры.