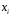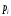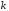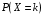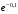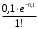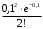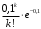Курсовая Теория Вероятностей и Математическая статика. ТипРасчёт_МоскалёвИван_АС-21. Теория вероятностей и математическая статика
 Скачать 424.3 Kb. Скачать 424.3 Kb.
|
|
Ответ: . №18 В ящике 2020 носков – синих и красных. Может ли синих носков быть столько, чтобы вероятность вытащить наудачу два носка одного цвета была равна 0,5? Решение Ответ: . №19 Гневные отзывы о работе интернет-магазина оставляют 80% недовольных покупателей (тех, кого плохо обслужили в магазине). Из числа довольных покупателей положительный отзыв оставляют только 15%. Некоторый интернет-магазин заработал 60 гневных и 20 положительных отзывов. Пользуясь этой статистикой, оцените вероятность того, что очередной покупатель останется доволен обслуживанием в этом интернет-магазине. Решение Пусть p – вероятность того, что покупателя обслужат хорошо, а 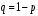 вероятность того, что плохо. Тогда вероятность того, что покупатель оставит хороший отзыв, равна 0,15p, а вероятность того, что будет плохой отзыв, равна вероятность того, что плохо. Тогда вероятность того, что покупатель оставит хороший отзыв, равна 0,15p, а вероятность того, что будет плохой отзыв, равна 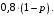 Тогда: Тогда: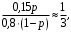 откуда откуда 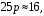 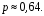 Ответ: 0,64. №20 Имеются три одинаковых на вид урны: в первой 2 белых шара и 3 чёрных, во второй – 4 белых и один чёрный, в третьей – три белых шара. Некто подходит наугад к одной из урн и вынимает из неё один шар. Пользуясь формулой полной вероятности, Найти вероятность того, что не менее 3-х ламп из 5 останутся исправными">найти вероятность того, что этот шар будет белым. Решение Существует 3 гипотезы: 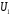 – выбор первой урны: – выбор первой урны: 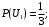 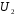 – выбор второй урны: – выбор второй урны: 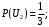 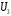 – выбор третьей урны: – выбор третьей урны: 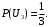 Интересующее нас событие А – вынутый шар окажется белым. Данное событие может произойти только с одной из гипотез: 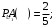 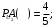 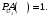 Тогда: Тогда: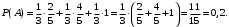 Ответ: 0,2. №21 Радиосообщение может быть передано днем (с вероятностью 3/4), либо ночью (с вероятностью 1/4). Из-за помех вероятность его успешного приема составляет днем 60%, а ночью 80%. Найти вероятность, что сообщение будет принято. Решение Ответ: . №22 Телеграфное сообщение состоит из сигналов «точка» и «тире». Статистические свойства помех таковы, что искажаются в среднем 2/5 сообщений «точка» и 1/3 сообщений «тире». Известно, что среди передаваемых сигналов «точка» и «тире» встречаются в соотношении 5:3. Определить вероятность того, что принят передаваемый сигнал, если: а) принят сигнал «точка»; б) принят сигнал «тире». Решение Пусть событие A – принят сигнал «точка», B – принят сигнал «тире». Отсюда следует 2 гипотезы: H1 – передан сигнал «точка», H2 – передан сигнал «тире». По условию 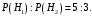 Кроме того, Кроме того, 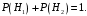 Поэтому, Поэтому, 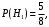 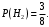 Известно, что: 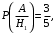 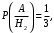 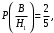 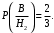 Вероятности событий A и B находим по формуле полной вероятности: 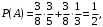 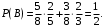 Искомые вероятности будут: а) 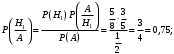 б) 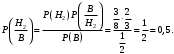 Ответ: а) 0,75; б) 0,5. №23 Пассажир может обратиться за получением билета в одну из трех касс. Вероятности обращения в каждую кассу зависят от их местоположения и равны соответственно р1, р2 р3. Вероятности того, что к моменту прихода пассажира имеющиеся в кассе билеты будут распроданы, равны: для первой кассы Р1, для второй Р2, для третьей Р3. Пассажир направился за билетом в одну из касс и приобрел билет. Найти вероятность того, что это была первая касса. Решение Ответ: . №24 По каналу связи передается 6 сообщений. Каждое из сообщений может быть искажено помехами с вероятностью 0,2 независимо от других. Найти вероятность того, что 1) хотя бы одно сообщение из 6 искажено; 2) не более 2 из 6 не искажены; 3) все сообщения переданы без искажения. Решение Так как вероятность искажения 0.2, то вероятность передачи сообщения без помех – 0,8. Используя формулу Бернулли, найдем вероятность того, что: хотя бы одно сообщение из 6 искажено: 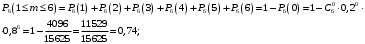 не более 2 из 6 не искажены: 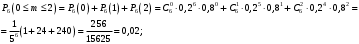 все сообщения переданы без искажения: 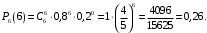 Ответ: 1) 0,74; 2) 0,02; 3) 0,26. №25 Производится стрельба по цели тремя снарядами. Снаряды попадают в цель независимо друг от друга. Для каждого снаряда вероятность попадания в цель равна 0,4. Если в цель попал один снаряд, он поражает цель (выводит ее из строя) с вероятностью 0,3; если два снаряда – с вероятностью 0,7; если три снаряда – с вероятностью 0,9. Найти полную вероятность поражения цели. Решение Ответ: . №26 Стоматологическая клиника распространяет рекламные листовки у входа в метро. Опыт показывает, что в одном случае из тысячи следует обращение в клинику. Найти вероятность того, что при распространении 50 тыс. листков число обращений будет: а) равно 41, б) находиться в границах от 36 до 47. Решение Имеем схему Бернулли с параметрами: 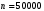 – количество распространенных листовок; – количество распространенных листовок;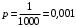 – вероятность обращения в клинику после получения листовки; – вероятность обращения в клинику после получения листовки;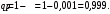 Событие А). Так как n достаточно велико, будем использовать приближенную формулу – локальную формулу Лапласа: 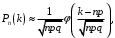 где k = 41, значения функции ϕ(x) берутся из таблицы. Получим: где k = 41, значения функции ϕ(x) берутся из таблицы. Получим: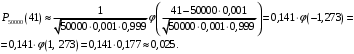 Событие Б). Так как n достаточно велико, будем использовать приближенную формулу – интегральную теорему Лапласа: 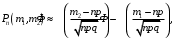 где где 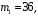 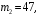 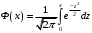 – функция Лапласа (значения берутся из таблиц). Получим: – функция Лапласа (значения берутся из таблиц). Получим: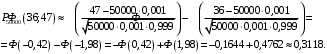 Ответ: а) 0,025; б) 0,3118. №27 В книге на 1000 страниц 100 опечаток. Какова вероятность обнаружить, в наудачу взятой странице, хотя бы одну опечатку? Решение По условию задачи предполагается, что число опечаток распределено по закону Пуассона. Так как в 1000 страницах имеется 100 опечаток, поэтому можно предположить, что 1 страница содержит 1 опечатку: 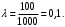 Если событие А – страница рукописи содержит хотя бы одну опечатку, то событие 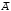 – страница рукописи, не содержащая ни одной опечатки, то есть 0 опечаток. Так как число опечаток распределено по закону Пуассона, то: – страница рукописи, не содержащая ни одной опечатки, то есть 0 опечаток. Так как число опечаток распределено по закону Пуассона, то: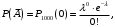 где где 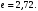 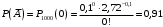 Так как события A и 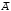 противоположны, то вероятность события A равна: противоположны, то вероятность события A равна: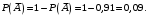 Ответ: 0,09. №28 Радист вызывает корреспондента, причем каждый последующий вызов производится лишь в том случае, если предыдущий вызов не принят. Вероятность того, что корреспондент примет вызов, равна 0,4. Составить закон распределения числа вызовов, если число вызовов не более 5. Найти математическое ожидание и дисперсию этой случайной величины. Решение 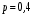 – примет вызов, – примет вызов, 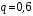 – не примет вызов. Х = {1,2,3,4,5} – число вызовов, – не примет вызов. Х = {1,2,3,4,5} – число вызовов, 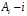 – вызов принят. – вызов принят.Вероятность того, что первый вызов принят: 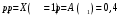 Второй вызов состоится лишь при условии, что первый вызов не принят: 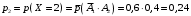 Для остальных также: 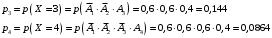 Пятый вызов при любом исходе (будет принят, не принят) – последний. Поэтому 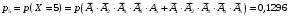
Проверим: 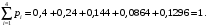 Математическое ожидание M(X) и дисперсию D(X) вычисляем по формулам: 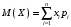 и и 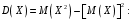 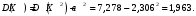 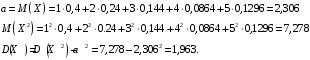 Ответ: 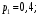 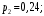 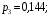 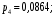 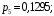 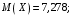 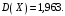 №29 Билет на электричку стоит 50 рублей, а штраф за безбилетный проезд – 450 рублей. Если безбилетник (заяц) попадается контролёру, то оплачивает и штраф, и стоимость билета. Известно, что контролёр встречается в среднем один раз на 10 поездок. Заяц ознакомился с основами теории вероятностей и решил придерживаться стратегии, которая делает математическое ожидание расходов наименьшим возможным. Как ему поступать: покупать билет каждый раз, не покупать никогда или бросать монетку – покупать билет или нет? Решение Пусть вероятность покупки билета p, а вероятность появления контролера q. Случайная величина X "Расходы на поездку" имеет распределение 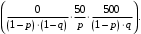 Математическое ожидание расходов: 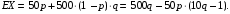 По условию 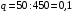 . Следовательно, . Следовательно, 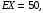 то есть не зависит от р. Отсюда появляется некое "равновесие" – средний расход на поездку не зависит от частоты или вероятности покупки билета. то есть не зависит от р. Отсюда появляется некое "равновесие" – средний расход на поездку не зависит от частоты или вероятности покупки билета.Ответ: Всё равно. №30 Дана функция распределения вероятностей:  Найти f(x), Р(3<Х<4), P(X<5), P(2,1 Решение Найдем функцию плотности распределения вероятностей: 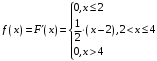 Построим графики F(x) и f(x): 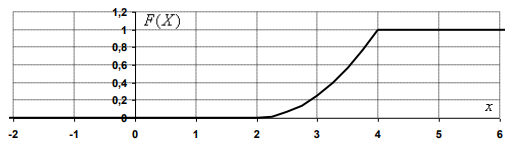 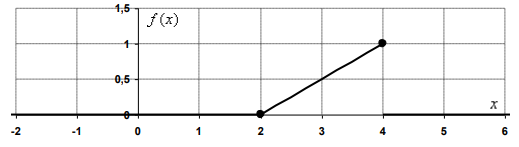 Вычислим вероятности попадания случайной величины X в интервалы: 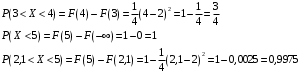 Ответ: 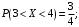 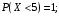 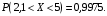 №31 Непрерывная случайная величина Х задана плотностью распределения вероятностей: 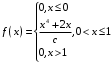 Найти 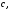 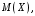 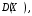 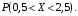 Решение Найдем коэффициент c. По свойству функции плотности распределения: 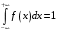 В данной задаче: 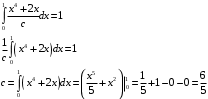 Таким образом, функция плотности распределения: 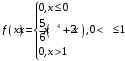 Вычислим математическое ожидание: 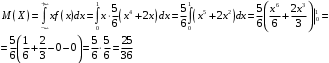 Дисперсию вычислим по формуле: 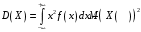 В данном случае: 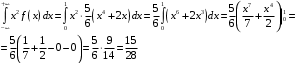 Таким образом, дисперсия: 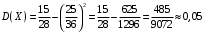 Найдем вероятность того, что случайная величина X примет значение из интервала (0,5; 2,5): 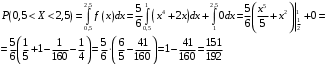 Ответ: 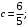 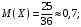 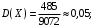 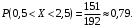 №32 Задана плотность вероятности f(x) случайной величины Х. 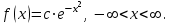 Определить: 1) коэффициент с; 2) функцию распределения F(x); 3) математическое ожидание М(Х); 4) дисперсию D(Х); 5) среднее квадратическое отклонение σ(Х); 6) вероятность попадания случайной величины Х в интервал (0;1). Решение Ответ: . №33 Задана плотность вероятности f(x) случайной величины Х. 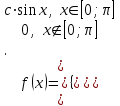 Определить: 1) коэффициент с; 2) функцию распределения F(x); 3) математическое ожидание М(Х); 4) дисперсию D(Х); 5) среднее квадратическое отклонение σ(Х); 6) вероятность попадания случайной величины Х в интервал (0;π/4). Решение Ответ: . №34 В тексте учебника по психологии содержатся опечатки: в среднем, одна на десять страниц. Пусть Х – число опечаток на одной странице. Определить закон распределения для Х. Найти вероятность, что на странице есть хотя бы одна опечатка. Решение По условию задачи можно сделать вывод, что случайная величина Х принимает значения 0, 1, 2… и распределена по закону Пуассона с параметром 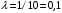 (среднее число опечаток на страницу). Тогда вероятности можно находить по формуле: (среднее число опечаток на страницу). Тогда вероятности можно находить по формуле: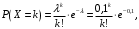 где где 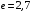 Получаем:
Найдем вероятность, что на странице есть хотя бы одна опечатка: 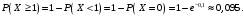 |