Курсовая Теория Вероятностей и Математическая статика. ТипРасчёт_МоскалёвИван_АС-21. Теория вероятностей и математическая статика
 Скачать 424.3 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ ДОНЕЦКОЙ НАРОДНОЙ РЕСПУБЛИКИ АВТОМОБИЛЬНО-ДОРОЖНЫЙ ИНСТИТУТ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Факультет «Дорожно-транспортный» Кафедра «Математическое моделирование» ТИПОВОЙ РАСЧЕТ по дисциплине «Теория вероятностей и математическая статика» Выполнил: студент II курса группы АС-21 Москалёв И.В. № зачетной книжки 21-006 Проверил: Заведующий кафедрой, профессор. д.т.н. Вовк Л.П. Горловка 2023 №1 Сколько различных дробей можно составить из чисел 3, 5, 7, 11, 13, 17 так, чтобы в каждую дробь входили 2 различных числа? Сколько среди них будет правильных дробей? Решение Различных дробей из 6 чисел: 3, 5, 7, 11, 13, 17 можно составить  шт. ( способами выбираем два числа из 6, и двумя способами составляем из них дробь: сначала одно число – числитель, другое знаменатель и наоборот).Из этих 30 дробей ровно 15 будут правильные (т.е., когда числитель меньше з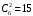наменателя):  способами выбираем два числа из 6, и единственным образом составляем дробь так, чтобы числитель был меньше знаменателя.Ответ: 30; 15. №2 Сколько существует шестизначных чисел, все цифры которых имеют одинаковую чётность? Решение Из нечетных цифр 56 т. к. 0 не может быть первым. Из чётных цифр: 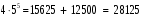 Ответ: 28125. №3 Сколько пар натуральных чисел удовлетворяет равенству 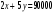 ?Решение 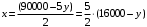 16000 – у кратно 2 и не равно 0, иначе х = 0, а 0 – не натуральное число. Поэтому у кратно 2 и принадлежит промежутку (0;16000). Найдём сколько чисел кратных 2 входит в этот промежуток:  Ответ: 8000. №4 Каждую клетку квадратной таблицы 2×2 можно покрасить в чёрный или белый цвет. Сколько существует различных раскрасок этой таблицы? Решение В каждой из 2х2 = 4 клеток может быть 2 варианта раскраски. То есть, есть 2 варианта раскраски первой клетки, на каждый из них есть по 2 подварианта раскраски второй клетки, на каждый из них по 2 подварианта для третьей и так же для четвёртой клетки. Получим: 2·2·2·2 = 16 вариантов. Ответ: 16. №5 Слово – любая конечная последовательность букв русского алфавита. Выясните, сколько различных слов можно составить из слов а) ВЕКТОР; б) ЛИНИЯ; в) ПАРАБОЛА; г) БИССЕКТРИСА; д) МАТЕМАТИКА. Решение а) Так как все буквы слова различны, то всего можно получить: 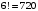 слов;б) В этом слове две буквы И, а все остальные буквы разные. Временно будем считать разными и буквы И, обозначив их через И1 и И2. При этом предположении получится 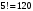 разных слов. Те слова, которые получаются друг из друга перестановкой букв И1 и И2, на самом деле одинаковы. Таким образом, полученные 120 слов разбиваются на пары одинаковых. Поэтому разных слов всего: 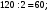 в) В этом слове 8 букв, три из которых А. Временно будем считать разными и буквы А, обозначив их через А1, А2 и А3. При этом предположении получится  разных слов. Те слова, которые получаются друг из друга перестановкой букв А1, А2 и А3, на самом деле одинаковы. Таким образом, полученные 3 слова разбиваются на 8 одинаковых. Поэтому разных слов всего: 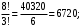 г) В этом слове три буквы С и две буквы И. Считая все буквы различными, получаем 11! слов. Отождествим слова, отличающиеся лишь перестановкой букв И, но не С: 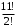 слов. Теперь отождествим слова, отличающиеся перестановкой букв С: 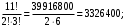 д) В этом слове три буквы А, две буквы Т и две буквы М. Считая все буквы различными, получаем 10! слов. Отождествим слова, отличающиеся лишь перестановкой букв Т и М, но не С: 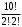 слов. Теперь отождествим слова, отличающиеся перестановкой букв С: 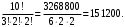 Ответ: а) 720; б) 60; в) 6720; г) 3326400; д) 151200. №6 Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево (например, таких как 54345, 17071)? 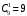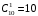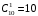Решение  способами можно выбрать цифру для разряда единиц и разряда десятков тысяч (ноль будет исключением, так как, если он находится в разряде десятков тысяч, то число не является пятизначным); способами можно выбрать цифру для разряда десятков и тысяч; способами можно выбрать цифру для разряда сотен.Таким образом, существует 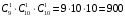 пятизначных чисел, которые одинаково читаются слева направо и справа налево.Ответ: 900. №7  Имеется электрическая цепь. Опишите, что: а) цепь будет работать, б) имеется разрыв цепи. Решение Ответ: . №8 В классе 16 учеников. Каждый месяц учитель делит класс на две группы. Какое наименьшее количество месяцев должно пройти, чтобы каждые два ученика в какой-то из месяцев оказались в разных группах? Решение Составим таблицу и разобьём класс на две группы так, чтобы любые два ученика в какой-то из четырех месяцев оказались в разных группах. В ней будут преобладать следующие значения: 0 – ученик входит в первую группу; 1 – ученик входит во вторую группу.
Так как в столбце можно расставить нули и единицы восемью различными способами, то в таблице найдутся два одинаковых столбца. Ученики, которым соответствуют эти столбцы, будут попадать в одну и ту же группу. 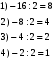 Ответ: 4 месяца. №9 Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Физик» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Физик» выиграет жребий ровно два раза. Решение Обозначим «+» такую сторону монеты, которая отвечает за выигрыш жребия «Физиком», другую сторону – «–», отвечающая за проигрыш. Всего возможно восемь комбинаций выпадения жребия: – – – 6. + – + – – + 7. + + – – + – 8. + + + – + + + – – Вариант «+» для Физика только два раза возможен в трёх случаях: + + – + – + – + + m = 3 – кол-во вариантов для Физика; n = 8 – общее кол-во вариантов.  Ответ: 0,375. №10 Найти вероятность того, что при бросании двух игральных костей выпадет от 7 до 10 очков. Решение Общее число исходов (возможных комбинаций цифр на двух игральных костях): 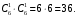 Подсчитаем количество благоприятствующих исходов: 7 очков: (1,6), (6,1), (2,5), (5,2), (3,4), (4,3); 8 очков: (2,6), (6,2), (3,5), (5,3), (4,4); 9 очков: (3,6), (6,3), (4,5), (5,4); 10 очков: (4,6), (6,4), (5,5) Всего: 18 благоприятствующих исходов. По классическому определению: 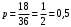 – искомая вероятность.Ответ: 0,5. №11 Петя предлагает Васе сыграть в следующую игру. Петя дает Васе две коробки с конфетами. В каждой из двух коробок шоколадные конфеты и карамельки. Всего в обеих коробках 25 конфет. Петя предлагает Васе взять из каждой коробки по конфете. Если обе конфеты окажутся шоколадными, то Вася выиграл. В противном случае выиграл Петя. Вероятность того, что Васе достанутся две карамельки, равна 0,54. У кого больше шансов на победу? Решение Поскольку Вася вынет две карамельки с вероятностью 0,54, то вероятность того, что он вынет две шоколадные конфеты: 1 – 0,54 = 0,46 Т.к. вероятность выигрыша для Васи меньше 0,5 (0,5 > 0,46), то больше шансов на победу у Пети. Ответ: больше шансов на победу у Пети. №12 На окружности радиуса R=2 наугад взято две точки. Какова вероятность того, что расстояние между ними не превышает π/6, если это расстояние отсчитывается на окружности как наименьшая из дуг, их соединяющая? Решение Ответ: . №13 На бесконечную шахматную доску со стороной квадрата а наудачу бросается монета радиуса  . Найти вероятности следующих событий: А = «монета попадет целиком внутрь одного квадрата», В = «монета пересечет не более одной стороны квадрата».Решение П 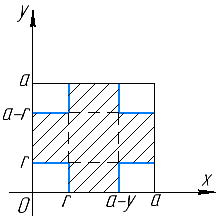 усть (х, у) – координаты центра упавшей монеты. В силу бесконечности шахматной доски можно считать, что элементарные исходы данного эксперимента полностью определяются положением центра упавшей монеты относительно вершин квадрата, содержащего этот центр. Помещая начало координат в одну из вершин указанного квадрата, можно записать множество элементарных исходов в виде   Множество, соответствующее событию   т.е. является квадратом со стороной  Следовательно      Ответ:   №14 Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,5. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза. Решение Если А играет белыми, то вероятность выигрыша 0,5 Если А играет черными, то вероятность выигрыша 0,3 Т.к. А играет и белыми, и черными, вероятность А выиграть 2 раза составит:  Ответ: 0,15. №15 Стрелок стреляет по мишени один раз. В случае промаха стрелок делает второй выстрел по той же мишени. Вероятность попасть в мишень при одном выстреле равна 0,7. Найдите вероятность того, что мишень будет поражена (либо первым, либо вторым выстрелом). Решение Вероятность того, что мишень будет поражена либо первым, либо вторым выстрелом, равна сумме вероятностей событий A и B, где A – попадание по мишени при первом выстреле; B – попадание по мишени при втором выстреле, учитывая, что при первом выстреле был промах. Вероятность события А:  Вероятность события B: 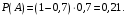 Искомая вероятность:  Ответ: 0,91. №16 В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода. Решение Для погоды на 4, 5 и 6 июля есть 4 варианта: ХХО, ХОО, ОХО, ООО (здесь Х – хорошая, О – отличная погода). Найдем вероятности наступления такой погоды:  Указанные события несовместные, вероятность их суммы равна сумме вероятностей этих событий:  Ответ: 0,392. №17 Известно, что на встречу выпускников Дедов придет с вероятностью p1, Ефимов – с вероятностью p2и Федоров – с вероятностью p3. Выпускники приходят на встречу независимо друг от друга. Найти вероятности событий: A= {пришли только двое из названных лиц}, B = {Дедов и Ефимов пришли на встречу}, C ={хотя бы один из названных лиц пришел на встречу}. Решение |